Algorithmus der Woche

• » Startseite
• » aktueller Algorithmus
• » Liste der Algorithmen

Informationen

• » Infoflyer Presse
• » Infoflyer Schule
• » Download Logo

Gimmicks für's Klassenzimmer

• » Visuelle Kryptographie

Links

• » Informatikjahr
• » Fakultätentag Informatik

Intern

• » Für Autoren
• » Für Organisatoren
• » Buchprojekt

Sonstiges

• » Impressum
• » Gästebuch
• » Haftung

In dieser Woche geht es darum, Zyklen in Graphen zu suchen. Das bedeutet, wir wollen feststellen, ob in einer Menge von Knoten, die durch Kanten miteinander verbunden sind, ein Zyklus enthalten ist. Ein Zyklus oder Kreis ist dabei ein Weg von einem Knoten zu sich selbst.

Szenario 1

Du bist mit dem Flugzeug mitten in einem Urwald abgestürzt, und suchst einen Weg zurück in die Zivilisation. Durch den Dschungel führen etliche Trampelpfade, die von Einheimischen angelegt wurden; außerhalb der Wege ist das Dickicht undurchdringlich. Durch das dichte Blätterdach kannst du nicht einmal die Sonne sehen. Du packst also die verfügbare Ausrüstung zusammen und marschierst in der erstbesten Richtung los. Schon nach wenigen Minuten kommst du an eine Weggabelung; du entschließt dich, den rechten Weg weiterzulaufen. Dann kommt eine Kreuzung, an der du geradeaus gehst. Leider ist das ein Holzweg, eine Sackgasse die nicht weiter führt. Also kehrst du um, gehst zur Kreuzung zurück und wendest dich nach rechts. Bei der nächsten Abzweigung gehst du nach links, dann wieder nach rechts und so weiter. Auf einmal lichtet sich der Urwald und du stehst - wieder vor deinem Flugzeug, von dem du losgelaufen bist: offenbar bist du die ganze Zeit im Kreis gelaufen. Wie kannst du verhindern, dass dir so etwas beim nächsten Versuch wieder passiert?

Szenario 2

Andy möchte mit Benny und Charly ins Kino gehen. Charly muss aber zu Hause Babysitten und kann nur dann weg, wenn Dany kommt und ihn ablöst. Benny darf erst los, wenn er seine Hausaufgaben erledigt hat. Dazu braucht auch er die Hilfe von Dany, die versprochen hat, zu ihm zu kommen, sobald sie das Aufgabenheft von Eddy zurückbekommt, das sie ihm in der Schule geliehen hatte. Eddy grübelt aber noch an den Aufgaben und hofft, dass Benny ihm eine Mail mit der Lösungsidee schickt. Warum wird Andy den Film wahrscheinlich verpassen?

Beide Szenarien können auf dasselbe Problem zurückgeführt werden, nämlich die Zyklensuche in Graphen. Ein (gerichteter) Graph ist eine Struktur bestehend aus Knoten und Kanten, wobei eine Kante jeweils von einem Knoten zu einem anderen Knoten führt. Knoten werden als Kreise gezeichnet, und Kanten als Pfeile zwischen zwei Knoten. Zum Beispiel könnten wir im zweiten Szenario für jede Person einen Knoten zeichnen, und eine Kante vom Knoten x zum Knoten y eintragen, wenn Person x auf Person y wartet. Das ergibt dann den folgenden Graphen:

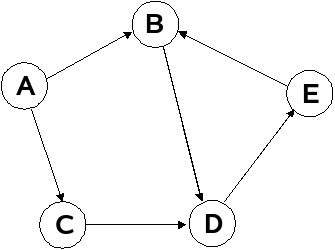
Wie man sofort sieht, gibt es hier einen Zyklus B D E B, d.h. eine Folge von Knoten, die durch Kanten verbunden sind, und der Anfang und das Ende der Folge sind derselbe Knoten. Benny wartet auf Dany, Dany wartet auf Eddy, und Eddy wartet auf Benny: Wenn sie nichts dagegen tun, werden sie so ewig warten. Solche Zyklen können leicht dazu führen, dass bestimmte Prozesse nie aufhören (wie im ersten Beispiel), oder gar nicht weiterkommen (wie im zweiten Beispiel). Wenn das bei einem Computer passiert, spricht man von einer Endlosschleife oder von einer Verklemmung. Beides führt meist dazu, dass das Programm keine Reaktion mehr zeigt und man es von außen abbrechen muss. Daher ist es oft eine wichtige Aufgabe, Zyklen zu erkennen (und nach Möglichkeit zu vermeiden).

Wie geht man jetzt zur Zyklensuche praktisch vor? Kommen wir zum Urwaldbeispiel zurück. Hier kannst du wie dereinst Hänsel und Gretel den Weg mit Steinchen markieren: Wenn du dann beim Laufen auf ein vorher hingelegtes Steinchen kommst, weißt du, dass du schon einmal da gewesen bist. Für eine systematische Suche nach einem Ausweg bringt dich also das letzte Wegstück nicht weiter, und du solltest besser umkehren. Um die Urwaldexpedition durch ein Computerprogramm zu simulieren, können wir unter anderem eine Tiefensuche verwenden (siehe auch den 5. Algorithmus der Woche: „Tiefensuche — Prinzessin Ariadne und Kaiser Franz“ von Michael Dom, Falk Hüffner und Rolf Niedermeier). Wir modellieren zunächst die Urwald-Landkarte durch einen Graphen: Jede Wegkreuzung oder –gabelung ist dann ein Knoten des Graphen, und jedes Wegstück zwischen zwei Verzweigungen ist eine Kante. Den Tiefensuchen-Algorithmus können wir wie folgt formulieren:

Anmerkung: Dieser Algorithmus ist rekursiv, das bedeutet rückbezüglich, formuliert: In der Definition der Prozedur wird auf die Prozedur selbst Bezug genommen. Auch eine solche Rekursion kann einen nicht anhaltenden Zyklus verursachen, wenn man nicht aufpasst. Ohne das Setzen von Markierungen würde dieser Algorithmus beispielsweise bei einem zyklischen Graphen unweigerlich in einen Zyklus geraten...

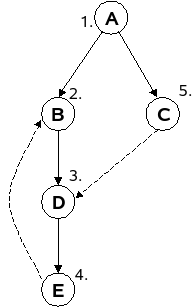Falls in diesem Algorithmus ein Knoten erreicht wird, der keine Nachfolger hat (eine Sackgasse), oder der schon bereits markiert ist, so wird die Suche nicht fortgesetzt sondern zum letzten Knoten zurückgekehrt Das nebenstehende Bild verdeutlicht den Ablauf des Algorithmus für den Graphen des zweiten Beispiels. Die Knoten sind dabei von oben nach unten gezeichnet, die Nummern geben die Reihenfolge an, in der die Knoten erreicht und markiert werden. Die Suche startet beim Knoten A, d.h. mit dem Aufruf Tiefensuche(A). Da A noch nicht markiert ist, werden nacheinander Tiefensuche(B) und Tiefensuche(C) aufgerufen. Die Bearbeitung des Aufrufs Tiefensuche(C)wird dabei zurückgestellt, bis die Ausführung von Tiefensuche(B) erledigt ist. Tiefensuche(B) ruft also zunächst Tiefensuche(D), dieses wiederum Tiefensuche(E), und dieses Tiefensuche(B). B ist allerdings schon markiert, also wird zu E zurückgekehrt. Hier sind schon alle Nachfolgerknoten verarbeitet, also erfolgt die Rückkehr zu D, dann zu B und A. Jetzt kann der zurückgestellte Aufruf von Tiefensuche(C) bearbeitet werden. Da D bereits markiert ist, erfolgt die Rückkehr zu C und A. Jetzt sind alle Aufrufe bearbeitet und die Ausführung des Algorithmus wird beendet.

Für die Zyklensuche muss der Algorithmus etwas modifiziert werden. Wie wir im obigen Beispiel sehen, gibt es drei Arten von Kanten:

1. Vorwärtskanten, z.B. von A nach C
2. Querkanten, z.B. von C nach D, und
3. Rückwärtskanten, z.B. von E nach B.

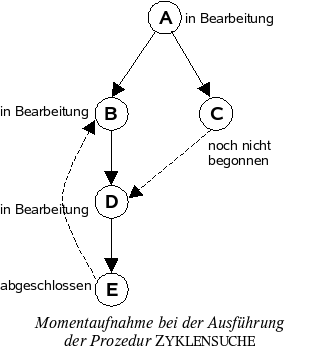
Nur eine Rückwärtskante kann einen Zyklus verursachen. Rückwärtskanten können von Querkanten unterschieden werden dadurch, dass sie auf einen Knoten verweisen, der bisher noch nicht vollständig abgearbeitet wurde. Wir können das dadurch berücksichtigen, dass wir die Markierung erweitern: statt einfach nur „unmarkiert“ oder „markiert“ merken wir uns in der Markierung jedes Knotens, ob die Bearbeitung noch nicht begonnen hat, der Knoten sich in Bearbeitung befindet, oder die Bearbeitung abgeschlossen ist.

Aufrufreihenfolge für den Beispielgraphen:

Zyklensuche (A) // A noch nicht begonnen
| A in Bearbeitung
| Zyklensuche (B) // B noch nicht begonnen
| | B in Bearbeitung
| | Zyklensuche (D) // D noch nicht begonnen
| | | D in Bearbeitung
| | | Zyklensuche (E) // E noch nicht begonnen
| | | | E in Bearbeitung
| | | | Zyklensuche (B) // B in Bearbeitung
| | | | | Zyklus gefunden!
| | | | E abgeschlossen // Zeitpunkt der Momentaufnahme
| | | D abgeschlossen
| | B abgeschlossen
| Zyklensuche (C) // C noch nicht begonnen
| | C in Bearbeitung
| | Zyklensuche (D) // D abgeschlossen
| | C abgeschlossen
| A abgeschlossen

Der angegebene Algorithmus stellt fest, ob vom Ausgangsknoten aus ein Zyklus erreicht werden kann. Man kann aber daran nicht erkennen, welche Knoten tatsächlich auf dem Zyklus liegen. Um das festzustellen, muss man sich den zurückgelegten Weg, das heißt die Folge der Knoten „in Bearbeitung“ merken. Bei der oben angegebenen Momentaufnahme ist der aktuelle Weg A B D E B , das heißt, B, D und E liegen auf dem Zyklus. Wenn man also auf einen Knoten stößt, bei dem man schon einmal war, so sind alle Knoten, die danach besucht wurden, in dem Zyklus enthalten. Falls die Suche bei einem Knoten abgeschlossen ist, man also zum darüber liegenden Knoten zurückkehrt, muss dieser Knoten natürlich auch aus dem aktuellen Pfad entfernt werden. Algorithmisch könnte das in etwa so aussehen:

Robert Tarjan hat diese Idee weiter ausgearbeitet und einen Algorithmus entwickelt, mit dem alle Zyklen „durchnummeriert“ werden können. Zyklen, die miteinander zusammenhängen, erhalten dabei die gleiche Nummer. Tarjan’s Algorithmus kann dazu verwendet werden einen Graphen in so genannte „starke Zusammenhangskomponenten“ zu zerlegen, also die Menge der Knoten so aufzuteilen, dass innerhalb der Teile jeder Knoten von jedem erreichbar ist.

Wie wir gesehen haben, ist die Tiefensuche gut geeignet, um alle Zyklen in einem Graphen zu finden. Falls es lediglich darum geht, festzustellen, ob ein gegebener Ausgangsknoten in einem Zyklus liegt, so können wir einen einfacheren Algorithmus verwenden: Wir können mittels einer so genannten Breitensuche die Menge der vom Ausgangsknoten erreichbaren Knoten berechnen. Dazu gehen wir davon aus, dass wir eine effiziente Methode haben, mit der wir für eine Menge von Knoten die Nachfolgermenge berechnen können, das heißt, die Menge der Knoten die durch eine Kante mit der ursprünglichen verbunden sind. Und dann starten wir einfach mit der Menge, die nur den Ausgangsknoten enthält, berechnen die Nachfolgermenge, die Nachfolger-Nachfolgermenge, davon wieder die Nachfolgermenge und so weiter, bis wir irgendwann entweder keinen neuen Knoten hinzubekommen, oder den Ausgangsknoten wieder erreichen.

Man kann sich eine Breitensuche in etwa wie die Ausbreitung von Wellen vorstellen, die von einem Stein ausgehen, der in einen ruhigen See geworfen wird. Die Wellenfront, also die vorderste Welle, umfasst jeweils den erreichbaren Teil der Wasseroberfläche.

Die im Breitensuchen-Algorithmus verwendete Schleife wird höchstens so oft wiederholt, wie es Knoten im Graphen gibt, üblicherweise jedoch viel weniger oft. Andererseits müssen bei der Breitensuche die beiden Mengen „Front“ und „Erreichbar“ angelegt und verwaltet werden, die (im Vergleich zur Tiefensuche) unter Umständen sehr viele Knoten enthalten können. Die Komplexität hängt sehr wesentlich von der Effizienz der verwendeten Mengenoperationen ab. Bei einigen Programmiersprachen gibt es sehr schnelle Bibliotheksfunktionen für große Mengen und Relationen.

Historische Notizen

Das Problem, Zyklen in Graphen zu suchen, ergab sich schon sehr früh in der Geschichte der Informatik. Erste Anwendungsbeispiele in den 1950-ern waren die Suche nach Schleifen in Schaltkreisen oder Datenflussdiagrammen. Die Tiefensuche und damit verbunden die rekursive Zyklensuche ist seit den 1960-ern bekannt und wird oft als Standardbeispiel für Backtracking-Algorithmen verwendet. Tarjan’s Algorithmus zur Berechnung von starken Zusammenhangskomponenten erschien 1972. Eine wesentliche Anwendung von Algorithmen zur Zyklensuche besteht in der Erkennung von Verklemmungen in Betriebsmittelgraphen: in jedem Mehrprozess-Betriebssystem können bei mangelnder Synchronisation zyklische Wartebedingungen auftreten. Bekannte Veranschaulichungen dafür sind Dijkstra’s Problem der dinierenden Philosophen oder Lamport’s Problem der Bäckereiwarteschlangen. Seit den 1970-ern tauchen immer wieder Computerspiele (z.B. „dungeons and dragons“) auf, in denen der Spieler durch ein virtuelles Labyrinth (einen Graphen) wandert, in dem diverse Gefahren zu bestehen sind. In den 1990-ern wurden neue effiziente Algorithmen und Datenstrukturen zur Zyklenerkennung im Rahmen von Zustandsraum-Suchverfahren bei der automatischen Verifikation von Modellen entwickelt.