Michael Dom, Friedrich-Schiller-Universität Jena
Falk Hüffner, Friedrich-Schiller-Universität Jena
Rolf Niedermeier, Friedrich-Schiller-Universität Jena
„Das eben geschieht den Menschen, die in einem Irrgarten hastig werden: Eben die Eile führt immer tiefer in die Irre.“
— Lucius Annaeus Seneca (4 n. Chr. – 65 n. Chr.)
Ariadne, nach griechischer Sage die Tochter von Minos, dem König von Kreta, verliebte sich in Theseus. Dieser Athener Held war beauftragt, den Minotaurus (ein Ungeheuer halb Mensch, halb Stier) zu töten. Die Herausforderung wurde ungleich größer dadurch, dass der Minotaurus im Labyrinth versteckt war. Die kluge Ariadne stattete ihren Helden mit einer Rolle Faden aus: Indem Theseus ein Fadenende am Eingang des Labyrinths festknotete und den Faden beim Durchforschen des Labyrinths abrollte, konnte er zum einen vermeiden, gleiche Teile des Labyrinths mehrfach zu durchsuchen, und zum anderen sicherstellen, auch wieder den Weg zurück in Ariadnes Arme zu finden – wobei zwischendurch der Minotaurus zu töten war.
Sehen wir uns die Suche im Labyrinth nun etwas genauer an: Anstatt eines Fadens genügt uns auch ein Stück Kreide; unser Labyrinth bestehe aus Kreuzungen und Gängen. Mit der Kreide markieren wir die von einer Kreuzung abgehenden Gänge, und zwar ein Haken für bereits einmal durchlaufene Gänge, und zwei Haken für „tote“ Gänge. Konkret lauten die Regeln für unsere Suche im Labyrinth:
- Befindet man sich in einer Sackgasse, so dreht man einfach um und geht zurück zur letzten Kreuzung.
- Hat man dagegen eine Kreuzung erreicht, malt man erst mal einen Haken an die Wand des Ganges, durch den man gekommen ist, um später ggf. wieder zurück finden zu können. Anschließend gibt es mehrere Möglichkeiten:
- Zunächst kontrolliert man, ob man im Kreis gelaufen ist: Wenn der Gang, durch den man gekommen ist, soeben seinen ersten Haken bekommen hat und wenn außerdem noch weitere Haken an anderen Gängen der Kreuzung sichtbar sind, so ist dies der Fall, und man macht einen zweiten Haken an den Gang und dreht um.
- Ansonsten prüft man, ob die Kreuzung noch unerkundete Gänge hat: Falls es noch Gänge ohne Markierungen gibt, so nimmt man von diesen den ersten von links und malt dort einen Haken an die Wand.
- Andernfalls hat man bereits alle von der aktuellen Kreuzung abgehenden Gänge untersucht, und man nimmt den Gang, der nur einen Haken hat (es sollte davon nur einen geben, denn haben alle Gänge bereits zwei Haken, so steht man wieder am Start, und es gibt keinen Ausgang aus dem Labyrinth).
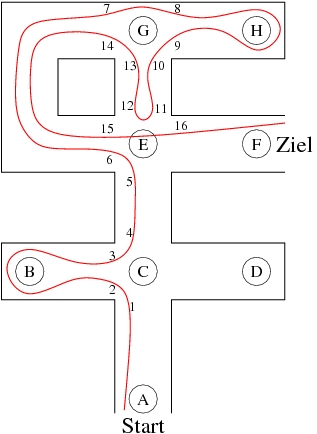Betrachten wir folgendes Beispiel, in dem wie
im Bild dargestellt ein Weg von A nach F gesucht wird. Wir gehen davon aus,
dass eine Sackgasse nur unmittelbar vor ihrem Ende als
solche erkannt werden kann.
Wir gehen los vom Start A Richtung Norden. Die erste Kreuzung ist C. Erst mal eine Markierung am Südausgang machen (1). Natürlich ist hier sonst noch keine Markierung, also nehmen wir den linkesten unmarkierten Weg, d.h. den in Richtung Westen, und markieren ihn (2). Dann bei B: eine Sackgasse – also umdrehen. Wieder bei C angelangt, hat der Weg nach Westen jetzt schon zwei Markierungen, der nach Süden eine, aber nach Norden ist noch gar nichts markiert, also geht es dort lang. Bei E ist wieder eine unberührte Kreuzung, und wir wählen unter den drei Möglichkeiten die nach Westen. Nach zwei Kurven gehen wir in G geradeaus über die Kreuzung, zwei Markierungen hinterlassend (7 und 8). Eine Sackgasse in H, also wieder umdrehen. In G ist nur eine Möglichkeit erlaubt: nach Süden zu E. Hier tritt zum ersten Mal die Regel gegen das Im-Kreis-Laufen in Kraft: wir haben beim Betreten von E einen Haken am Nordausgang gemacht (11); außerdem existiert an dieser Kreuzung bereits eine Markierung am Südausgang (5) und eine am Westausgang (6) – demnach müssen wir also umdrehen. Über die Kreuzung G und zwei Kurven geht es zurück, so dass nun der nördliche Teil komplett abgesucht ist und wir wieder bei E landen. Nach Osten gibts hier noch gar keine Markierung, also da lang. Schließlich erreichen wir in F das Ziel.
Das Prinzip, das wir bei unserer Suche verwendet haben, nennt sich Tiefensuche: Wie gesehen, gehen wir immer möglichst tief in das Labyrinth hinein. Erst wenn wir dabei auf eine Sackgasse stoßen, gehen wir zur letzten Kreuzung zurück und versuchen es von dort aus erneut.
Die Regeln für eine Tiefensuche sind so einfach, dass man sie mit wenigen Zeilen einem Computer beibringen kann. Dabei merkt man sich für jede Kreuzung einen „Zustand“, wobei am Anfang alle Kreuzungen „unentdeckt“ sind. Wird die Suche an einer Kreuzung X gestartet, so markiert die Tiefensuche-Funktion zunächst die Kreuzung X als „entdeckt“ und ruft dann für alle noch nicht erkundeten benachbarten Kreuzungen sich selbst auf (dies ist ein beim Programmieren häufig benutzter Trick namens „Rekursion“). Bemerkt man, dass man im Kreis gelaufen ist, so kehrt man einfach zur aufrufenden Funktion per „return“ zurück.
Das Verfahren Tiefensuche funktioniert nicht nur für Labyrinthe, sondern findet auch in deutlich anderen Zusammenhängen Anwendung, wie z.B. in folgendem Fall: Wie allseits bekannt, ist Kaiser Franz ein sehr gewissenhafter Obertan der Fußballwelt. Die korrekte Informationsvermittlung in Sachen Fußballweltmeisterschaft liegt ihm sehr am Herzen. Dazu wird er natürlich alle relevanten Informationsquellen auf unseriöse Berichterstattung abklopfen, insbesondere auch die freie Internet-Enzyklopädie Wikipedia. Franz stellt also folgende Aufgabe: Durchmusterung aller Web-Seiten der Wikipedia, die untereinander verlinkt sind und das Thema „Fußball-WM“ behandeln. Auch hier liegt die Schwierigkeit darin, einerseits nicht endlos im Kreis zu laufen und andererseits alles gewissenhaft und regelmäßig zu überprüfen. Dies lässt sich wiederum effektiv erledigen mit Hilfe von Tiefensuche im Geflecht der einzelnen Web-Seiten der Wikipedia, ausgehend von der Startseite „Fußball-Weltmeisterschaft“.
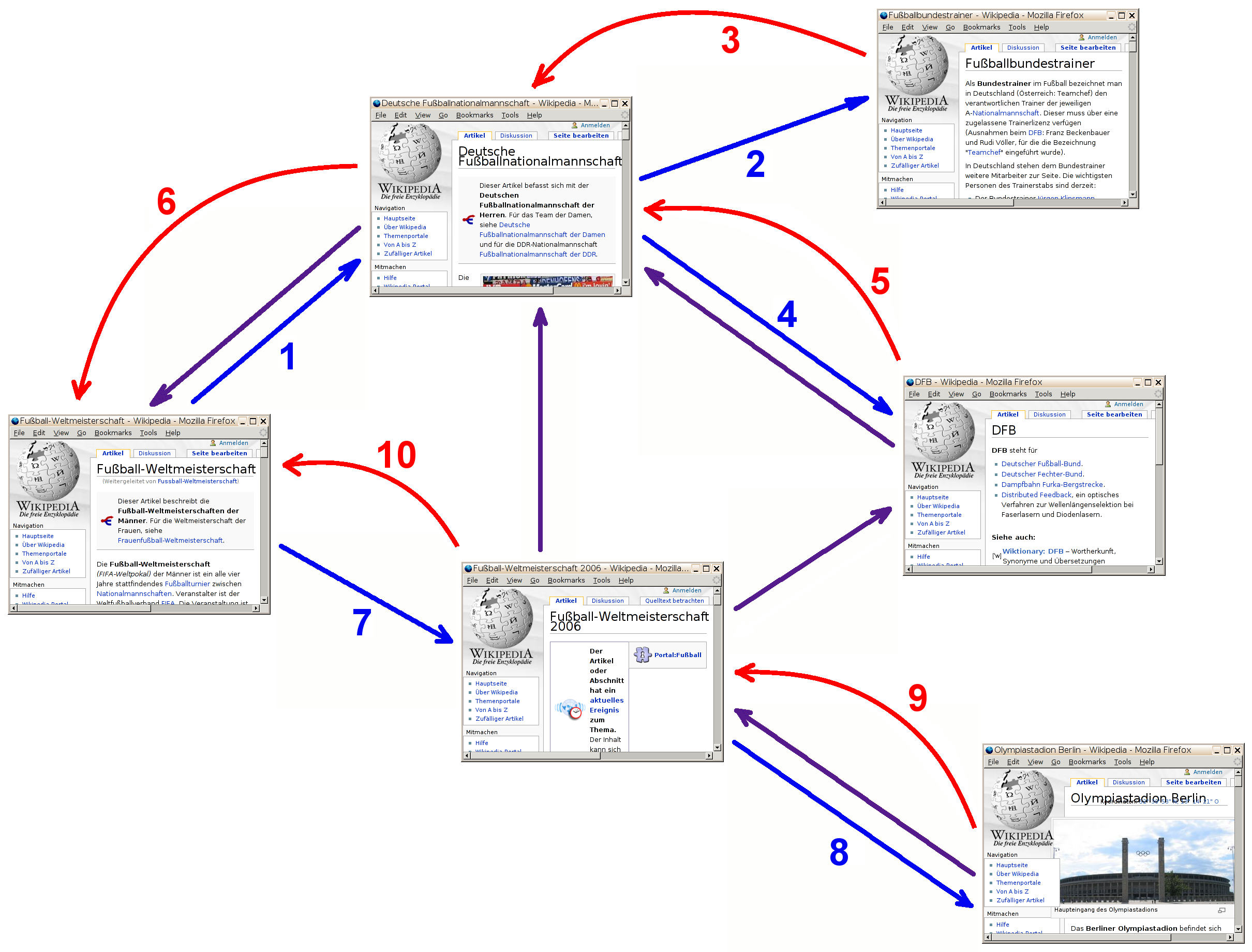
Wolfis Tiefensuche in der Wikipedia: Die Zahlen verdeutlichen die Reihenfolge der Sprünge von Seite zu Seite. Ein gerader Pfeil bedeutet, dass eine Seite einen Link auf eine andere Seite enthält. Gebogene Pfeile bedeuten, dass Wolfi an dieser Stelle den „Zurück“-Knopf benutzt. Man beachte, dass Wolfi nicht alle dargestellten Links anklickt, da ja manche davon zum Zeitpunkt seines Besuchs bereits in violett angezeigt werden.
Nehmen wir an, Wolfi stelle sich der von Franz gestellten Aufgabe. Nachdem er die Seite „Fußball-Weltmeisterschaft“ kontrolliert hat, klickt er auf den erstbesten für die WM relevanten Link dieser Seite und landet z.B. auf der Seite „Deutsche Fußballnationalmannschaft“ (siehe Bild). Auch diese Seite wird von ihm kontrolliert, und weiter gehts mit dem erstbesten Link dieser Seite, wobei er jedoch darauf achtet, keinen Link anzuklicken, der zu einer Seite führt, die er bereits besucht hat – solche Links erkennt Wolfi als geübter Web-Surfer daran, dass sie im Browser in violett anstatt in blau erscheinen (diese hilfreiche Funktion des Browsers entspricht also gewissermaßen dem Malen von Kreidehaken in unserem ersten Beispiel). Wenn Wolfi schließlich eine Seite erreicht, die nichts mehr mit der Fußball-WM zu tun hat oder wenn alle relevanten Links einer Seite abgearbeitet (d.h. besucht und daher violett dargestellt) sind, so klickt er auf den „Zurück“-Knopf seines Browsers und fährt mit den Links der nun angezeigten Seite fort.
Irgendwann landet Wolfi beim Klicken auf den „Zurück“-Knopf zum wiederholten Male auf seiner Startseite „Fußball-Weltmeisterschaft“, und alle Links der Seite sind violett gefärbt, d.h. schon besucht. Dies bedeutet für Wolfi Feierabend, denn mit seiner auf den ersten Blick chaotisch erscheinenden Vorgehensweise hat er alle Seiten der Wikipedia besucht, die von der Seite „Fußball-Weltmeisterschaft“ aus direkt oder indirekt über Links zu erreichen sind und mit der Fußball-WM zu tun haben.
Abschließend noch ein paar kurze Bemerkungen zu Vor- und Nachteilen des algorithmischen Verfahrens „Tiefensuche“. Vorteile sind die sehr einfache Implementierung auf Rechnern sowie die meist effiziente Ausführbarkeit: Letzteres ergibt sich aus der Beobachtung, dass jeder Gang des Labyrinths höchstens zweimal durchlaufen wird und somit die Gesamtlaufzeit der Tiefensuche selbst im ungünstigsten Fall proportional zur Gesamtganglänge des Labyrinths ist. Ein Nachteil der Tiefensuche ist, dass man mit ihr im Allgemeinen nicht die kürzeste Verbindung zum Ziel findet – und in unendlichen Strukturen vielleicht nie (da man unendlich lange in der falschen Richtung suchen kann). Das könnte mit der etwas komplizierteren und meist aufwändigeren „Breitensuche“ nicht passieren – aber das ist ein anderes Thema, wie auch die weiteren Aktivitäten von Ariadne und Franz.
„Alles auf Erden lässt sich finden, wenn man nur zu suchen sich nicht verdrießen lässt.“
— Philemon von Syrakus (um 360 v. Chr. – 264 v. Chr.)