Autoren
Burkhard Monien, Universität Paderborn
Ulf Lorenz, Universität Paderborn
Daniel Warner, Universität Paderborn
Schon seit langer Zeit sind die Menschen von der Idee begeistert, Maschinen Gesellschaftsspiele spielen zu lassen. Unermüdlich sollen sie sein, aber auch spielstark, damit es nicht so schnell langweilig wird. Besonders das Schachspiel scheint hierbei magische Anziehungskraft zu besitzen.
Ende des 18. Jahrhundert war z.B. der Schachtürke von Wolfgang von Kempelen eine Sensation in Europa. Es handelte sich dabei um einen angeblich vollautomatischen mechanischen Schachspieler, dessen Funktionsgeheimnis lange Zeit gewahrt wurde. Jahrzehntelang soll er die Menschen seiner Zeit in Erstaunen versetzt haben, darunter prominente Namen wie Napoleon, Edgar Allen Poe und Kaiserin Maria Theresia. 1854 kam das gute Stück bei einem Brand "ums Leben". Natürlich handelte es sich bei dieser Maschine um einen Trick: ein kleinwüchsiger Mensch konnte sich so geschickt im Inneren verstecken, dass es sehr schwierig war ihn zu entdecken, selbst wenn man den Spieltisch scheinbar aufmachte.

Bild: Der Schachtürke
Bildnachweis: Jan Braun / Heinz Nixdorf MuseumsForum
Mit der Erfindung von Computern gab es neue Hoffnung auf eine echte Schachmaschine. Viele Jahre hatte man es für nahezu unmöglich gehalten, dass ein Computer besser Schach spielen könnte als die besten Menschen. Aber heute wissen wir es besser. Mit Garry Kasparov musste sich Ende des 20. Jahrhunderts erstmals ein Schachweltmeister einem Schachprogramm, der IBM-Maschine Deep Blue, in einem Kampf über sechs Spiele knapp geschlagen geben. Als Nachfolgemodell im Jahr 2005 gilt der Schachcomputer Hydra, der einen bislang einmaligen Vorsprung vor allen anderen Schachprogrammen und Menschen herausgearbeitet hat.
Die Frage ist nun, wie funktioniert eigentlich ein Schachprogramm?
Zunächst muss man natürlich ein Modell des Schachspiels in den Rechner hineinbringen. Das kann man z.B. tun, indem man das 8x8 Felder große Schachbrett als 2-dimensionales 8x8 Array darstellt und den einzelnen Figuren Zahlen zuordnet. Ein leeres Feld entspricht einer 0, ein weißer Bauer einer 1, usw.
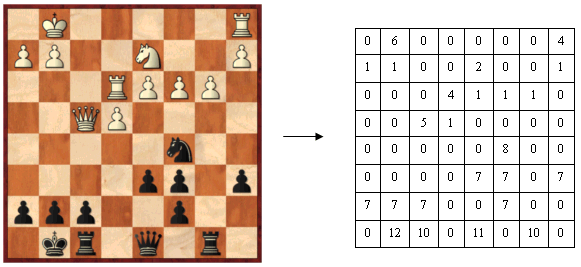
Das Schachprogramm lässt sich nun grob in drei "Baugruppen" unterteilen: den Zuggenerator, die Bewertungsprozedur und den Suchalgorithmus. Der Zuggenerator erzeugt zu einer vorgegebenen Stellung eine Liste aller dort möglichen Züge. Die Bewertungsprozedur ordnet einer ihr vorgegebenen Schachstellung eine Zahl zu. Je größer diese Zahl ist, desto besser steht der Weiße, negative Zahlen geben einen schwarzen Vorteil wieder.

Obige Abbildung zeigt, wie eine Stellungsbewertung aufgebaut sein kann. Typische Werte für die so genannten "Materialwerte" sind +100 Punkte für einen weißen, bzw. -100 Punkte für einen schwarzen Bauern. Dann +/-300 für Springer und Läufer, +/-500 für Türme und +/-1000 für Damen. Da die Abbildung ein ausgeglichenes Materialverhältnis zeigt ist die Summe der Figurenwerte gleich 0. Dem gegebenen Schema nach hätte Weiß also einen Vorteil von 124 Punkten.
Außerdem vergeben wir noch die Werte -∞ für "Schwarz gewinnt ganz sicher" und ∞ für "Weiß gewinnt ganz sicher". Das ist z.B. dann der Fall, wenn wir eine Stellung betrachten, in der einer der Spieler matt gesetzt wurde. Das Zeichen "∞" wird auch als "unendlich" bezeichnet, ihr braucht euch aber nicht den Kopf über "Unendlichkeit" zu zerbrechen. Denkt euch stattdessen einfach, dass es sich um eine sehr große Zahl handelt; so groß, dass "Schwarz gewinnt ganz sicher" oder "Weiß gewinnt ganz sicher" damit ausgedrückt werden können.
Der wichtigste Teil eines Spielprogramms ist aber der so genannte Suchalgorithmus, der eine intelligente Vorausschau organisiert, indem er einen "Spielbaum" auswertet. Ein Spielbaum ist dabei die Struktur, die entsteht, wenn wir uns vorstellen, welche Züge wir in einer während des Spiels entstandenen Situation ausführen könnten, welche Antworten unser Gegner daraufhin ausspielen könnte, wie unsere eigene Antwort wiederum aussehen könnte, usw. Die nachfolgende Abbildung skizziert diese Vorstellung.

Beispiele dieser Art werden schnell unübersichtlich. Deshalb gehen wir im folgenden davon aus, dass uns unsere Bewertungsprozedur für diejenigen Stellungen, für die keine Nachfolgestellungen abgebildet sind, die Werte 0 bzw. -∞ liefert. Für die anderen Stellungen kennen wir die Werte zunächst nicht. Wohin soll der Weiße dann ziehen? Falls er nach links zu (*) geht, darf Schwarz den nachfolgenden Zug wählen, und natürlich ginge der zu dem am weitesten rechts liegenden Nachfolger von (*). Schwarz würde in der Stellung (*) gewinnen, und deshalb hat die Stellung den Wert -∞. Der Wert der Stellung (*) kann also dadurch gebildet werden, dass wir ihr den kleinsten Wert der Nachfolgestellungen von (*) zuordnen.
Geht man von der Stellung (**) nach links, darf der Weiße den nachfolgenden Zug wählen. Einer davon hat den Wert 0, der andere -∞. Käme es zu dieser Stellung würde Weiß natürlich nach links ziehen, so dass die Stellung ausgeglichen bliebe. Der Wert des linken äußeren Nachfolgers der Stellung (**) wird deshalb gebildet, indem man den größten Wert von dessen Nachfolgestellungen heranzieht. Betrachten wir nun wieder die Stellung (**). Offenbar haben alle Nachfolgestellungen den Wert 0, und weil der kleinste Wert dementsprechend auch 0 ist, hat (**) den Wert 0. An der Ausgangsstellung darf Weiß wählen, und er sollte dorthin ziehen, wo er am meisten erreichen kann, also nach rechts. Die Ausgangsstellung ist eine ausgeglichene Stellung, was sich auch dadurch äußert, dass der größte (größere) Wert der Stellungen (*) und (**) gleich 0 ist.
Man nennt das vorgestellte Schema, den Stellungen Werte zuzuordnen das "Minimax-Prinzip". Der Begriff bedeutet "Minimum und Maximum bilden", und die Begriffe Minimum bzw. Maximum kommen aus dem lateinischen und bedeuten "das Größte" bzw. "das Kleinste". Eine einfache Möglichkeit, die Werte der Stellungen im Spielbaum zu ermitteln ist es, von unten nach oben, ausgehend von den Endstellungen ohne Nachfolger, den jeweiligen Vorgängern Werte gemäß diesem Minimax-Prinzip zuzuordnen. Den besten Zug findet man dann an der Ausgangsstellung, indem man die möglichen Folgestellungen und deren Werte betrachtet und einen Zug zu demjenigen Nachfolger auswählt, der einem gemäß dieser Werte am besten gefällt.
Im Folgenden geht es darum, einen pfiffigen Algorithmus zu erklären, der den besten Zug an der Ausgangsstellung ermittelt, ohne den ganzen Baum zu untersuchen. Und weil Spielbäume sehr schnell sehr unübersichtlich werden, sollten wir uns im Folgenden auf die für uns wichtigen Aspekte von Spielstellungen konzentrieren. Anstatt uns Spielbäume wie in obiger Abbildung als "Schachbäume" vorzustellen, stellen wir uns die Stellungen besser als Quadrate und Kreise vor, je nachdem ob der Weiße oder der Schwarze am Zug ist. Der Spielbaum des obigen Beispiels sieht dann wie folgt aus:

Außerdem sollten wir die Ausdrücke "Stellungen, bei denen Weiß am Zug ist" und "Stellungen, bei denen Schwarz am Zug ist" sinnvoll abkürzen. Nennen wir sie doch einfach Max-Stellungen (Quadrate) und Min-Stellungen (Kreise). So, jetzt sieht der Spielbaum doch schon viel übersichtlicher aus, und man kann schön sehen, dass der Weiße an der Wurzel nach rechts ziehen sollte, um das Spiel in eine ausgeglichene Stellung zu bringen.
Der Algorithmus der Wahl, um einen Min-/Max-Spielbaum zu durchsuchen, ist der Alphabeta-Algorithmus. Der ist etwas trickhaft, ihr solltet genau aufpassen!
Stell dir vor, du bekommst folgenden Auftrag:
Du bekommst von einem Auftraggeber eine Schachstellung und die Information, wer am Zug ist, sowie ein seltsames Zettelchen, auf dem zwei Zahlen stehen. Das sieht folgendermaßen aus: [Zahl1, Zahl2], und bedeutet, dass dein Auftraggeber sich nur dann für den exakten Wert der vorgegebenen Spielstellung interessiert, wenn der Wert zwischen den zwei gegebenen Zahlen liegt.
Dazu ein kleines Beispiel. Nehmen wir an, auf dem Zettelchen steht [-5,2]. Falls der echte Wert z.B. -1 ist, sollst du genau diesen Wert -1 liefern. Falls er aber außerhalb dieses so genannten Fensters liegt, und z.B. -6 ist, reicht es zu sagen, dass der Wert kleiner oder gleich -5 ist. Liegt der Wert auf der anderen Seite außerhalb des Fensters, (ist er also z.B. 10), so genügt es, zu sagen, dass der Wert größer oder gleich 2 ist.
Du sollst nun den Wert der Schachstellung bestimmen, sofern dieser in dem gegebenen Fenster liegt. Ansonsten sollst du herausfinden, ob der Wert der Schachstellung kleiner als Zahl1 oder größer als Zahl2 ist. Du darfst dir dazu einen Helfer heranziehen. Außerdem hilft dir dein Lehrer, der zu manchen Schachstellungen den Wert aus seiner langjährigen Schachspielerfahrung kennt.Falls der Lehrer den Wert kennt, gibst du diesen Wert an deinen Auftraggeber und bist fertig.
Sonst:Schreibe alle möglichen Züge, die in deiner Spielstellung möglich sind, auf ein Stück Papier. Bearbeite die Züge auf deiner Liste einen nach dem anderen auf folgende Weise:
Falls Weiß am Zug ist, gehst du so vor:
Zunächst gibst du deinem Helfer diejenige Stellung, die entsteht, wenn der Zug, den du gerade betrachtest, ausgeführt wird. Außerdem machst du ihm eine Kopie von deinem Zettel mit [Zahl1,Zahl2]. Du erklärst ihm genau, worum es geht, und dass er nach demselben Schema seine Spielstellung bewerten soll, wie du es für deine Stellung tust. Dann wartest du, bis er mit dem Ergebnis zu dir kommt. Falls der Wert, den er dir zurück gibt, größer ist, als deine Zahl1, überpinselst du die Zahl1 mit Tipp-Ex und ersetzt sie durch das Ergebnis deines Helfers. Sah z.B. dein Zettel so aus

und liefert dir dein Helfer eine 0 zurück, sieht dein Zettel jetzt so aus:

Falls deine neue Zahl1, also die linke Zahl auf deinem Zettel größer oder gleich der Zahl2 ist, gibst du Zahl1 als Ergebnis an deinen Auftraggeber zurück und hörst auf. Wenn du schlau warst, hast du mit dem Auftraggeber eine Belohnung ausgehandelt und gehst jetzt kassieren. Falls die neue Zahl1 immer noch kleiner als die Zahl2 ist, nimmst du dir den nächsten Zug deiner Liste und gehst wieder zu Zeile 4.
Falls in deiner Stellung Schwarz am Zug ist, und nicht Weiß, wie in Zeile 4 angenommen, verhältst du dich ganz ähnlich:
Zunächst gibst du deinem Helfer diejenige Stellung, die entsteht, wenn der Zug, den du gerade betrachtest, ausgeführt wird. Außerdem machst du ihm eine Kopie von deinem Zettel mit [Zahl1,Zahl2]. Du erklärst ihm genau, worum es geht, und dass er nach demselben Schema seine Spielstellung bewerten soll, wie du es für deine Stellung tust. Dann wartest du, bis er mit dem Ergebnis zu dir kommt. Falls der Wert, den er dir zurück gibt, kleiner ist, als deine Zahl2, überpinselst du die Zahl2 und ersetzt sie durch das Ergebnis deines Helfers.
Falls deine neue Zahl2, also die rechte Zahl auf deinem Zettel kleiner oder gleich der Zahl1 ist, gibst du Zahl2 als Ergebnis an deinen Auftraggeber zurück und hörst auf. Vergiss nicht die Belohnung zu kassieren. Falls die neue Zahl2 immer noch größer als die Zahl1 ist, nimmst du dir den nächsten Zug deiner Liste und gehst wieder zu Zeile 5.
An diese Stelle kommst du nur, wenn du für alle Züge deiner Liste Ergebnisse von deinem Helfer bekommen hast. Wenn Weiß am Zug ist, gibst du Zahl1 als Ergebniswert an deinen Auftraggeber. Falls Schwarz am Zug ist, gibst du ihm deine Zahl2.
Die Zahl1 wird typischerweise "alpha" genannt und die Zahl2 "beta". Deshalb besitzt der hier vorgestellte Algorithmus den Namen Alphabeta-Algorithmus. Der Algorithmus verwendet das Prinzip der Rekursion (vgl. z.B. Schnelle Sortieralgorithmen), und im Wesentlichen handelt es sich um eine sogenannte Tiefensuche, die einen Spielbaum von links nach rechts durchläuft. Das Besondere an dieser Tiefensuche ist, dass der Algorithmus in linken Teilen des Baums Informationen sammeln kann, die er dazu benutzt, um in rechten Teilbäumen Knoten nicht untersuchen zu müssen. Es gibt dabei keine Qualitätsverluste. Schauen wir uns dazu zunächst ein sehr kleines Beispiel an. Der Spielbaum soll wie folgt aussehen:

Die Stellungen sind jetzt mit S1 bis S7 bezeichnet. Der Algorithmus läuft zuerst links herunter bis zu S4, denn der Auftraggeber an S1 beauftragt seinen Helfer, sich S2 anzusehen, und der beauftragt wiederum seinen Helfer zu allererst einmal, sich S4 anzusehen. Weil S4 keine Nachfolger besitzt, kann der zweite Helfer unseren Lehrer nach dem Wert fragen. Der sagt uns z.B. den Wert 4.

Für S2 wissen wir nun, dass der Wert von S2 kleiner oder gleich 4 sein muss, da der Schwarze einen Nachfolger mit minimalem Wert wählt. Danach geht es zu Stellung S5, wo wir eine 3 bekommen, und wir wissen für S2, dass der Wert 3 ist. Zurück in Stellung S1, wissen wir, dass der Wert von S1 größer oder gleich 3 ist, denn wenn der Weiße an S1 nach links geht, wird er den Wert 3 erreichen. Was ihn erwartet, wenn er nach rechts geht, wissen wir noch nicht.
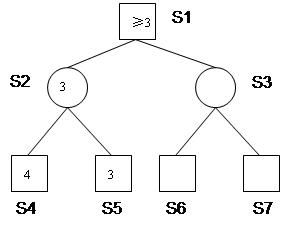
Jetzt kommt die Besonderheit des Algorithmus. Wir sind während des ganzen Beispiels noch gar nicht auf die "seltsamen" Parameter Zahl1 und Zahl2 (bzw. auch alpha und beta genannt) eingegangen, weil sie bis hierher noch nicht interessant waren. Mit Hilfe dieser Parameter wird dem Sachbearbeiter für Stellung S3 die Information mitgegeben, dass der gesamte Unterbaum unter S3 für den Auftraggeber in S1 (und damit für die gesamte Rechnung) nur interessant ist, wenn der Wert von S3 größer als 3 ist. Das Zahlenpaar [Zahl1,Zahl2], bzw. [3,∞] wird dem Helfer, der S3 bearbeiten soll also von oben mitgegeben. In der Algorithmus-Beschreibung geschieht das mit Hilfe der Zettelchen. Im Detail sieht das so aus, dass derjenige Sachbearbeiter, der für die Spielstellung S1 ursprünglich [-∞,∞] auf seinem Zettel stehen hatte, seine Zahl1 für S1 mit Hilfe von Zeile 4a (vgl. oben) auf 3 erhöht hat. Da die Bedingung ("Falls deine neue Zahl1, also die linke Zahl auf deinem Zettel größer oder gleich der Zahl2 ist...") in Zeile 4b nicht wahr ist, und die Stellung S3 noch untersucht werden muss, nimmt sich der Sachbearbeiter von Stellung S1 auch noch den zweiten möglichen Zug vor und geht wieder zu Zeile 4. Er beauftragt dann seinen Helfer S3 zu untersuchen und gibt ihm diesmal einen Zettel mit [3,∞] mit auf den Weg.

Wenn S3 untersucht wird, und ausgehend von dort S6, und in S6 z.B. der Wert 2 gefunden wird, dann wissen wir, dass der Wert von S3 kleiner oder gleich 2 ist. Wenn der für S3 verantwortliche Helfer Zeile 5a bearbeitet, wartet er dort auf seinen eigenen Helfer und bekommt von dem den Ergebniswert 2 mitgeteilt. Er setzt seine Zahl2 ebenfalls auf 2. Zusammenfassend ist dem Sachbearbeiter von S3 jetzt bekannt, dass der Wert von S3 höchstens 2 ist, und dass der genaue Wert von S3 für seinen Auftraggeber in S1 nur von Interesse wäre, wenn der Wert größer als 3 wäre.
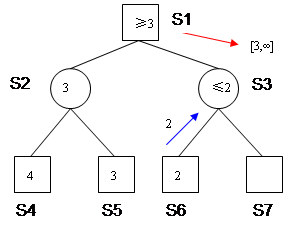
Das aber heißt, dass, egal was in S7 für ein Wert gefunden würde, die Stellung S3 die Entscheidung des Weißen an S1 nicht mehr beeinflussen kann. Dann brauchen wir S7 auch nicht zu untersuchen! Man sagt, der Knoten S7 wird durch die Anweisung in Zeile 5b "weggeschnitten".
Der entscheidende Clue eines Schachprogramms ist es, mit Hilfe von Spielbäumen möglichst weit in die Zukunft zu schauen. Dabei bewertet das Programm Stellungen, die es aus Zeitgründen nicht weiter verfolgen kann mit Hilfe von Schätzwerten einer Bewertungsprozedur, und rechnet diese Werte dem Minimax-Prinzip folgend zur Ausgangsstellung zurück. In der Tat kann man aufgrund der Baumbeschneidungen mit Hilfe des Alphabeta-Algorithmus doppelt so weit "in die Zukunft schauen" als wenn man den ganzen Baum durchsuchte. Das ist besonders beeindruckend, wenn man bedenkt, dass die Spielstärke von Schachprogrammen maßgeblich davon abhängt, wie weit sie vorausrechnen können. Zur Einschätzung: Wenn ein modernes Schachprogramm bis zu einer nominellen Tiefe von 20 rechnet, schlägt es jeden Menschen beim Turnierschach mehr oder weniger regelmäßig. Ohne Alphabeta-Algorithmus könnte es nur 10 Züge vorausschauen und hätte damit gerade einmal die Spielstärke eines Spielers der 2. Bundesliga.
Im Folgenden findest du noch ein Applet, das den Ablauf des Alphabeta-Algorithmus detailliert auf verschiedenen Beispielbäumen visualisiert. Für diejenigen von euch, die bereits eine Programmiersprache kennen, haben wir den Algorithmus zusätzlich in einer Schreibweise ähnlich zu einem Computerprogramm aufbereitet.
- Prof. Dr. rer. nat. Burkhard Monien
- Dr. rer. nat. Ulf Lorenz
- Daniel Warner

