Helmut Alt, FU Berlin
Heute stellen wir zwei Sortieralgorithmen vor, die zunächst recht ungewöhnlich erscheinen, die aber, falls man sehr große Mengen von Objekten sortieren will, eine viel schnellere Laufzeit haben als die bisher vorgestellten.
Algorithmus 1
Stelle dir das Problem so vor, dass du von einem Meister einen Stapel von Karten erhältst, die jeweils mit einer Zahl beschriftet sind. Du sollst diese Karten mit von unten nach oben sortierten Beschriftungen zurückgeben. Dies wird so gemacht:
Falls der Stapel nur aus einer Karte besteht, gib ihn sofort zurück, andernfalls:
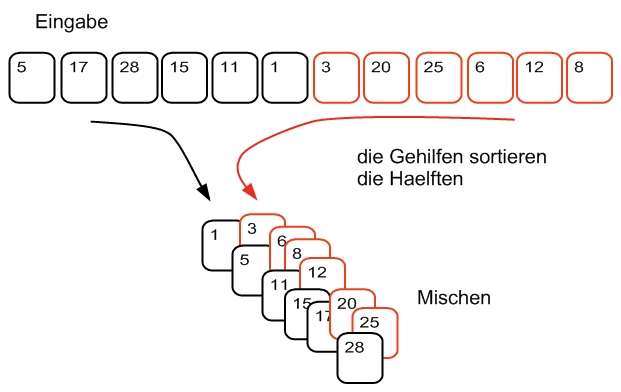
Teile den Stapel in zwei möglichst gleich große Teile. Gib jeden Teil je einem Gehilfen mit der Bitte, ihn ebenfalls genau nach dem hier beschriebenen Verfahren zu sortieren.
Warte bis dir beide Gehilfen die sortierten Teile zurückgegeben haben. Dann durchlaufe beide Stapel gleichzeitig von oben nach unten, und mische die Karten nach einer Art Reißverschlussprinzip zu einem sortierten Gesamtstapel zusammen. Gib diesen an deinen Meister zurück.
Wir demonstrieren das Vorgehen dieses Algorithmus’ an einem Beispiel:
Algorithmus 2
Stelle dir das Problem so vor, dass du von einem Meister einen Stapel von Karten erhältst, die jeweils mit einer Zahl beschriftet sind. Du sollst diese Karten mit von unten nach oben sortierten Beschriftungen zurückgeben. Dies wird so gemacht:
Falls der Stapel nur aus einer Karte besteht, gib ihn sofort zurück, sonst tue folgendes:
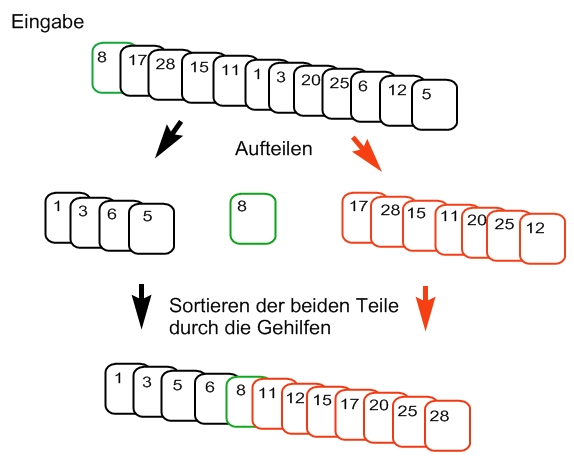
Nimm die erste Karte aus dem Stapel. Durchlaufe die restlichen Karten und teile sie auf in alle mit einem Wert kleiner oder gleich dem der ersten Karte (Stapel 1) und mit Wert größer als dem der ersten Karte (Stapel 2). Gib die beiden so entstandenen Teilstapel, wenn sie überhaupt Karten enthalten, an je einen Gehilfen mit der Bitte, sie ebenfalls genau nach dem hier beschriebenen Verfahren zu sortieren.
Warte bis dir beide Gehilfen die sortierten Teile zurückgegeben haben, dann lege zuunterst den sortierten Stapel 1, darauf die anfangs gezogene Karte, darauf den sortierten Stapel 2 und gib das Ganze als sortiert zurück.
An einem Beispiel demonstriert sieht dies so aus:
Erläuterungen zu unseren Sortieralgorithmen
Natürlich kann man diese Algorithmen nicht nur mit Stapeln von Karten mit Zahlen ausführen, sondern mit allen Objekten, die sich miteinander der Größe nach vergleichen lassen. Zum Beispiel kann man auch eine Balkenwaage nehmen und, nach diesen Algorithmen vorgehend, eine Menge von Objekten dem Gewicht nach sortieren.
Die Beschreibung zeigt, dass man zum Ausführen von Algorithmen natürlich nicht unbedingt einen Computer braucht. Zum besseren Verständnis empfehlen wir, beide Algorithmen "von Hand" auszuführen, indem man selbst die Rolle der verschiedenen "Gehilfen" übernimmt.
In allen höheren Programmiersprachen (z.B. C, C++, JAVA) gibt es diese Möglichkeit, dass eine Prozedur "sich selbst" aufruft. Man nennt dieses Konzept Rekursion und es hat eine sehr wichtige Funktion in der Informatik. Die Vorgehensweise, ein größeres Problem dadurch zu lösen, dass man es in kleinere Teilprobleme zerlegt, diese rekursiv löst und die entstehenden Teillösungen zu einer Gesamtlösung zusammenfügt, nennt man in der Informatik "divide and conquer". Unsere beiden Algorithmen funktionieren nach diesem Prinzip und es lässt sich auf viele, sehr unterschiedliche Probleme erfolgreich anwenden
Der erste der beiden Algorithmen heißt MergeSort. Er war bereits dem berühmten Mathematiker John von Neumann (1903 - 1957) bekannt in einer Zeit, als es Informatik als eigenes Fach noch nicht gab, und wurde bereits in mechanischen Sortiergeräten eingesetzt. Der zweite Algorithmus heißt QuickSort. Er wurde von dem berühmten britischen Informatiker C.A.R. Hoare bereits 1962 entwickelt.
Natürlich fragt man sich, warum man zum Sortieren, das doch scheinbar ein so einfaches Problem ist, solch merkwürdige Algorithmen nehmen sollte. Dies hat einen einfachen Grund: MergeSort und QuickSort sind für große Mengen von Daten wesentlich schneller als die einsichtigeren Sortieralgorithmen, die wir in der Woche zuvor vorgestellt haben. Wer sich mehr engagieren will und programmieren kann, kann ja auch einmal Programme für diese Algorithmen schreiben und sie experimentell mit den Programmen für MergeSort und QuickSort, die zum Teil auf den oben genannten Webseiten angegeben sind, vergleichen. Wie lange laufen die einzelnen Programme, wenn man sie 1000, 10000, 100000 ... Zahlen sortieren lässt? Auch wenn man die verschiedenen Algorithmen bei den oben angegebenen Animationen für Eingaben, die aus 100 oder 200 zu sortierenden Objekten bestehen, laufen lässt, merkt man schon deutlich den Unterschied.
Es ist möglich, mit mathematischen Methoden herzuleiten, wie die Laufzeit der Algorithmen von der Anzahl n der zu sortierenden Elemente abhängt. Dabei stellt sich heraus, dass ein einfacher Sortieralgorithmus, wie zum Beispiel das so genannte SortiereDurchEinfuegen eine Laufzeit hat, die proportional zu n2 ist während, die von MergeSort proportional zu n · log n ist, wobei log n der Logarithmus von n zur Basis 2 ist. Da die erste Funktion wesentlich stärker wächst als die zweite (Wie viel ist z.B. 10242 und wie viel ist 1024 · log 1024?), ist für große Mengen von Daten MergeSort wesentlich schneller.
Für QuickSort ist die Situation schwieriger. Man kann zeigen, dass seine Laufzeit für bestimmte Eingaben, zum Beispiel wenn die Eingabefolge schon sortiert ist, auch sehr langsam, das heißt proportional zu n2, ist. Ihr bekommt eine Vorstellung davon, warum dies so ist, wenn ihr ihn einmal auf einer solchen Eingabe "von Hand" ausführt. Wählt man aber statt des ersten Elements x zum Aufspalten der Folge irgendeines per Zufall aus der Folge, so ist die Wahrscheinlichkeit, dass der Algorithmus langsam ist, sehr gering. Im Mittel ist die Laufzeit auch proportional zu n · log n und QuickSort gilt in der Praxis als der schnellste Sortieralgorithmus.

