Autoren
Friedhelm Meyer auf der Heide, Universität Paderborn
Joachim Gehweiler, Universität Paderborn
Ich habe diesen Sommer mein Abi gemacht und möchte zum Herbst mit dem Studium beginnen – Informatik natürlich! Da es in meinem kleinen Ort keine Uni gibt, werde ich deshalb in Kürze umziehen müssen. Dann heißt es, all die tausend Sachen in meinen Schränken und Regalen in Umzugskartons zu verpacken. Um den Umzug möglichst kostengünstig zu gestalten, werde ich mich dabei bemühen, die Gegenstände in möglichst wenige Kartons zu verpacken.

Wenn ich nun alle Gegenstände einfach so der Reihe nach aus den Regalen nehmen und in einen Umzugskarton nach dem anderen verpacken würde, würde ich dabei eine ganze Menge Platz in den Kartons verschwenden, da die Gegenstände verschieden groß und unterschiedlich geformt sind, und sich dadurch eine Menge Lücken in dem Umzugskartons ergeben würden.
Die optimale Lösung für dieses Problem, d.h. die kleinstmögliche Anzahl benötigter Umzugskartons, würde ich sicherlich finden, wenn ich alle Möglichkeiten, die Gegenstände in Umzugskartons zu verpacken, der Reihe nach ausprobiere. Doch das würde bei so vielen Gegenständen eine halbe Ewigkeit dauern und obendrein ein riesiges Chaos in der Wohnung verursachen.
Deshalb würde ich die Gegenstände schon am liebsten in der Reihenfolge in Umzugskartons verpacken, in der sie mir beim Ausräumen der Schränke und Regale zufällig gerade in die Hand kommen. Die entscheidende Frage ist daher, wie viele Umzugskartons ich bei dieser Vorgehensweise mehr benötige als bei der optimalen Lösung. Um dies herauszufinden, werde ich das Problem nun analysieren.
Das Online-Problem „billig umziehen“
Da ich die Gegenstände der Reihe nach aus den Schränken bzw. Regalen nehmen und verpacken möchte, bedeutet das, dass ich es mit einem Online-Problem (vgl. Einführung in Online Algorithmen) zu tun habe, denn:
Die relevanten Daten (hier: die Größe der einzelnen Gegenstände) treffen erst nach und nach im Laufe der Zeit ein. Die Liste dieser Größen, in der Reihenfolge ihres Auftretens, bezeichnen wir im Folgenden mit s.
Es liegen keine Informationen über die zukünftigen Daten (hier: die Größen der noch nicht betrachteten Gegenstände) vor.
Die Anzahl der zu bearbeitenden Daten (hier: der zu verpackenden Gegenstände) ist nicht im Voraus bekannt.
Die aktuelle Anfrage muss sofort bearbeitet werden (hier: Gegenstände werden nicht vorübergehend zur Seite gelegt).
In der Realität liegen für einige Aspekte zwar Schätzwerte vor, da ich in der Wohnung schließlich jahrelang gelebt habe und somit eine gewisse Vorstellung davon habe, was sich alles in den Regalen und Schränken befindet; dies werde ich hier jedoch außer Acht lassen und das Problem somit idealisiert betrachten.
Meine Verpack-Strategie sieht nun als Online-Algorithmus folgendermaßen aus: Die Eingabe besteht aus einer Liste der Gewichte der zu verpackenden Gegenstände und die Ausgabe aus der Anzahl der benötigten Umzugskartons (n).
Algorithmus NextFit
Mit etwas mehr Aufwand kann man auch folgendermaßen vorgehen: ich könnte die Umzugskartons erst zum Schluss endgültig schließen und beim Verpacken eines jeden Gegenstands alle angefangenen Umzugskartons darauf überprüfen, ob vielleicht noch genügend Platz übrig ist. Dies hätte dann einen Vorteil, wenn ich für einen besonders großen Gegenstand einen neuen Umzugskarton anfangen muss, und danach wieder eine Reihe kleinerer Gegenstände zu verpacken sind, denn diese kleineren Gegenstände können eventuell noch in einem früheren Umzugskarton Platz finden.
Als Online-Algorithmus sieht diese zweite Strategie folgendermaßen aus:
Algorithmus FirstFit
Analyse der Algorithmen
Um die Analyse, wie gut oder schlecht meine Strategien funktionieren, etwas zu vereinfachen, nehme ich im Folgenden an, dass ein Gegenstand genau dann in einen Umzugskarton passt, wenn das noch unbenutzte Volumen des Umzugskartons größer oder gleich dem Volumen des zu verpackenden Gegenstands ist (ich vernachlässige also den aufgrund von „Verschnitt“ nicht nutzbaren Platz in den Umzugskartons). Weiterhin wähle ich die Volumeneinheit derart, dass die Kapazität der Umzugskartons genau 1 ist (und die Größen der zu verpackenden Gegenstände somit kleiner oder gleich 1 sind).
Um ein Gefühl für die Güte des Ergebnisses meiner Online-Algorithmen zu bekommen, schaue ich mir ein paar Beispiele an. Sind alle Gegenstände gleich groß – wie in Beispiel 1 – so liefern NextFit und FirstFit beide das optimale Ergebnis:
|
Beispiel 1: s = ( NextFit = FirstFit: 5 Kartons
|
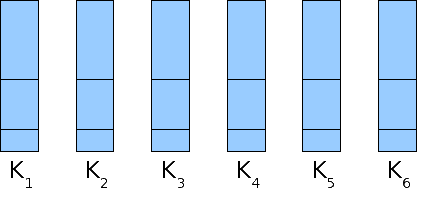
In Beispiel 2 liefern NextFit und FirstFit ebenfalls noch beide das optimale Ergebnis:
|
Beispiel 2: s = ( NextFit = FirstFit: 5 Kartons
|
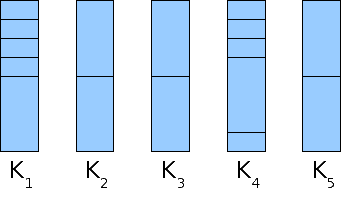
Beispiel 3 jedoch zeigt, dass die Reihenfolge der Gegenstände das Ergebnis beeinflussen kann – hier schneidet NextFit deutlich schlechter ab:
|
Beispiel 3: s = ( NextFit: 8 Kartons
FirstFit: 5 Kartons
|
Wählt man in Beispiel 3 anstatt der Größe 1/8 eine viel kleinere Zahl, so steigt der ungenutzte Platz pro Umzugskarton in NextFit sogar auf fast die Hälfte. Die Strategie NextFit verbraucht im Extremfall also fast doppelt so viele Umzugskartons wie bei optimaler Packung nötig wären.
Die Strategie FirstFit hat in Beispiel 3 zwar noch optimal abgeschnitten, doch auch für FirstFit gibt es ungünstige Eingaben, wie Beispiel 4 zeigt:
|
Beispiel 4: s = (0.15, 0.15, 0.15, 0.15, 0.15, 0.15, 0.34, 0.34, 0.34, 0.34, 0.34, 0.34, 0.51, 0.51, 0.51, 0.51, 0.51, 0.51) FirstFit: 10 Kartons
Optimal: 6 Kartons
|
Hier ergibt sich also ein Verhältnis von 10:6 für FirstFit gegenüber der optimalen Packung, d.h. FirstFit benötigt 1,67-mal so viele Umzugskartons. Wir nennen einen solchen Algorithmus 1,67-kompetitiv. Allgemein heißt eine Online-Strategie k-kompetitiv, wenn man nie mehr als das k-fache dessen benötigt, was man benötigt hätte, wenn man die Zukunft gekannt hätte. Wir nennen k auch die „Approximationsgüte“ der Strategie.
Es stellt sich nun die Frage, ob die Negativbeispiele 3 und 4 bereits die schlechtestmöglichen Eingabelisteen für NextFit bzw. FirstFit darstellen, oder ob es noch schlimmer kommen kann. Um die Approximationsgüte von NextFit zu berechnen, machen wir uns klar, dass die Gegenstände in je zwei benachbarten Kartons zusammen mehr Volumen ausmachen als ein Karton (wäre dies nicht der Fall, hätte NextFit die Gegenstände nicht auf zwei Kartons verteilt). Folglich ist jeder Karton im Durchschnitt mehr als halb voll, womit sich eine Approximationsgüte von 2 ergibt. Ein mathematisch exakter Beweis kann in der ausführlichen Version dieses Artikels nachgelesen werden.
Der Online-Algorithmus NextFit ist also 2-kompetitiv (vgl. Einführung in Online Algorithmen). Da dieser Beweis auf FirstFit übertragbar ist, ist somit auch FirstFit 2-kompetitiv. Mit einem deutlich komplizierteren Beweis (den wir hier nicht vorführen, vgl. weiterführende Materialien) kann man sogar zeigen, dass FirstFit 1,7-kompetitiv ist.
Wie gut kann ein Online-Algorithmus für Bin Packing sein?
Wir kennen nun die Approximationsgüte von NextFit bzw. FirstFit und wissen, dass es Eingabelisteen gibt, für die das Ergebnis fast einen Faktor 2 bzw. 1,7 vom theoretischen Optimum entfernt ist. Auf der einen Seite ist dies ein gutes Ergebnis, da wir wissen, dass der verschwendete Platz in den Umzugskartons niemals einen bestimmten Faktor überschreitet, andererseits ist es das Ergebnis aber auch etwas unbefriedigend, denn es macht schon einen schmerzlichen Unterschied, ob der Umzug nun 1000 EUR oder 2000 EUR (bzw. 1700 EUR) kostet.
Um nun abschließend zu beurteilen, wie gut oder schlecht die Verpackungsstrategien tatsächlich sind, gilt es noch zu untersuchen, wie gut ein Online-Algorithmus für dieses Problem überhaupt sein kann. Denn da die Eingabeliste nicht im Voraus bekannt ist, dürfte es wohl unmöglich sein, einen Online-Algorithmus zu entwerfen, der immer ein optimales Ergebnis liefert. Man kann beweisen, dass dies auch tatsächlich der Fall ist. Dazu überlegt man sich, dass eine c-kompetitive Online-Strategie auch für jede Teileingabe c-kompetitiv sein muss. Angenommen, man hat eine Eingabeliste, die aus einer Reihe von Gegenständen, die ein wenig kleiner als 1/2 sind, gefolgt von ebensovielen Gegenständen, die minimal größer als 1/2 sind, besteht. Dann werden bei der optimalen Lösung in jeden Karton jeweils einer der kleineren und einer der größeren Gegenstände verpackt. Dieselbe Online-Strategie kann aber nicht gleichzeitig auch für die Teileingabe, die nur aus der ersten Hälfte der Eingabe besteht, optimal arbeiten; denn in diesem Fall müßten bei der optimalen Lösung jeweils zwei der Gegenstände, die ein wenig kleiner als 1/2 sind, in einen Karton verpackt werden. Da man aber nicht im Voraus weiß, ob und wie viele größere Gegenstände in der Eingabeliste noch folgen, kann keine Online-Strategie in beiden Fällen ein optimales Ergebnis liefern. Damit erhalten wir folgendes Resultat (ein mathematisch exakter Beweis kann in der ausführlichen Version dieses Artikels nachgelesen werden):
|
Satz: Es gibt keinen Online-Algorithmus für das Bin Packing Problem, der besser als 4/3-kompetitiv ist. |
Unter dem Aspekt, dass selbst die bestmögliche Online-Strategie für das Umzugsproblem nicht besser als 4/3-kompetitv sein kann, erscheint nun die 1,7-kompetitve Strategie FirstFit in einem ganz anderen Licht. Na dann kanns mit dem Packen ja losgehen!
Eine weitere Einsatzmöglichkeiten des Bin Packing ist beispielsweise, Dateien auf CDs zu verteilen (etwa im Rahmen einer Datensicherung). In diesem Fall lassen sich die oben beschriebenen Strategien sogar direkt anwenden, d.h. man muss keine vereinfachende Annahmen bzgl. des „Verschnitts“ treffen, da dieses Problem bei Datenströmen nicht auftritt.


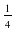 ,
, 
 ,
,  ,
, 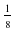 ,
,