Autoren
Susanne Albers, Universität Freiburg
Swen Schmelzer, Universität Freiburg

In diesem Jahr möchte ich nach längerer Pause wieder in den Skiurlaub fahren. Leider sind mir meine alten Skier zu klein, und so stehe ich vor der Frage, ob ich mir Skier leihen oder doch lieber kaufen soll. Wenn ich sie mir leihe, so muss ich pro Tag 10 Euro Leihgebühr zahlen. Für die 7 Tage meines Urlaubs würde ich also 70 Euro zahlen. Wenn ich mir Skier kaufe, so fallen Kosten von 140 Euro an. Vielleicht fahre ich aber in den nächsten Jahren öfter in den Skiurlaub. Da wäre es ja besser, wenn ich mir ein Paar kaufe. Wenn ich aber keinen Spaß mehr daran habe, wäre es besser, nur die geringeren Leihkosten zu zahlen. Die untere Abbildung zeigt die Gesamtkosten für das einmalige Kaufen und das tägliche Leihen, wenn man an genau x Tagen Skier benötigt.
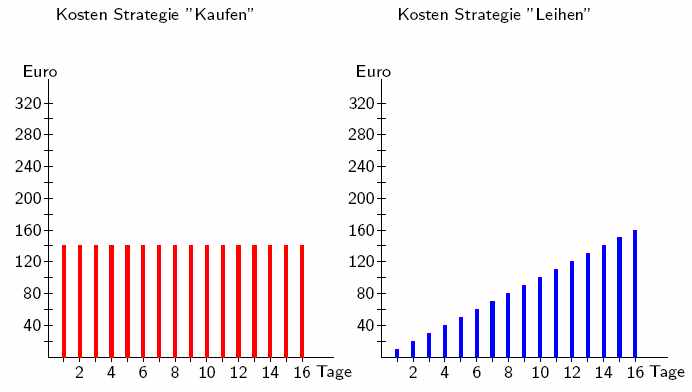
Ohne zu wissen, wie oft ich Ski fahren gehe, kann ich wohl nicht verhindern, etwas mehr zu bezahlen. Hinterher ist man immer schlauer. Aber wie kann ich verhindern, dass ich hinterher sage: "Ich hätte ja für weniger als die Hälfte Ski fahren können."? Probleme dieser Art bezeichnet man in der Informatik als Online-Probleme. Bei diesen muss man Entscheidungen treffen, ohne die Zukunft zu kennen. In unserem Fall wissen wir nicht, wie oft wir in der Zukunft Ski fahren werden, müssen aber entscheiden, ob wir Skier leihen oder kaufen. Würden wir die Zukunft kennen, so könnten wir leicht eine Entscheidung treffen. Fahren wir an weniger als 14 Tagen Ski, so ist es preiswerter, Skier zu leihen. Bei genau 14 Tagen bezahlt man in beiden Fällen gleich viel. Bei mehr als 14 Tagen sollten wir die Skier kaufen. Hat man vollständige Kenntnis über die Zukunft, so spricht man auch von einem Offline-Problem. In diesem Fall können wir, wie oben beschrieben, leicht die minimalen Kosten bestimmen. Wir können die minimalen Kosten mit einer Funktion f beschreiben. Dabei gibt x die Anzahl der Tage an, an denen wir Skier benötigen.
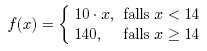
In einem Online-Algorithmus muss man zu jedem Zeitpunkt mit dem bisherigen Kenntnisstand eine Entscheidung treffen. Wenn wir uns am ersten Tag entscheiden, Skier zu leihen, so stehen wir am zweiten Tag wieder vor der gleichen Entscheidung. Wenn man mit einer Online-Strategie nie mehr als das Doppelte dessen bezahlt, was man bezahlt hätte, wenn man die Zukunft gekannt hätte, nennt man das 2-kompetitiv (wettbewerbsfähig). Allgemein heißt eine Online-Strategie k-kompetitiv, wenn man nie mehr als das k-fache dessen bezahlt, was man bezahlt hätte, wenn man die Zukunft gekannt hätte. Wir wollen für unser Problem eine 2-kompetitive Online-Strategie entwickeln.

In der obigen Abbildung ist links der optimale Wert (die Funktion f) rot dargestellt. In blau sind im rechten Koordinatensystem die Kosten unseres Online-Algorithmus aufgetragen. An der Grafik ist leicht zu erkennen, dass wir nie mehr als doppelt so viel wie das Optimum zahlen. Geht man an weniger als 14 Tagen fahren, zahlt man so viel, wie man auch bezahlt hätte, wenn man vorher gewusst hätte, wie oft man fahren wird. Geht man öfter, so bezahlt man nie mehr als das Doppelte.

Unser Problem haben wir damit zufriedenstellend gelöst. Was aber passiert bei anderen Leih- und Kaufkosten? Müssen wir unsere Strategie dann ändern? Um zu erkennen, dass die vorgeschlagene Strategie für beliebige Werte von Leih- und Kaufkosten 2-kompetitiv ist, normiere man die Kosten so, dass das Leihen von Skiern 1 Euro und das Kaufen n Euro kostet. Unsere Online-Strategie kauft am n-ten Tag, wenn die gesamten Leihkosten gerade n-1 betragen. Die Abbildung oben veranschaulicht, dass bei x<n Tagen die Online-Strategie optimale Kosten erzeugt. Bei x>=n sind die erzeugten Kosten weniger als doppelt so hoch wie das Optimum. Wir sind also 2-kompetitiv.
Das ist ja schon ganz nett, aber eigentlich würden wir gern näher am Optimum sein. Leider ist das nicht möglich. Kaufen wir zu einem anderen Zeitpunkt, so gibt es immer mindestens einen Fall, in dem wir mindestens doppelt so viel wie das Optimum zahlen müssten. Kauft man früher, zum Beispiel bereits am 11. Tag, so bezahlt man 240 Euro statt der notwendigen 110 Euro. Kauft man später, zum Beispiel erst am 17. Tag, so bezahlt man 300 Euro statt 140 Euro. In beiden Fällen liegt man damit über dem Doppelten der notwendigen Kosten. Kein Online-Algorithmus ist also besser als 2-kompetitiv.
Seitenwechselproblem:
Ein wichtiges Online-Problem der Informatik, das intern in einem Computer ständig auftritt, ist das Seitenwechselproblem. Hier muss stets entschieden werden, welche Speicherseiten im Hauptspeicher eines Computers und welche auf Festplatte gehalten werden. Der Prozessor eines Rechners kann auf den Hauptspeicher sehr schnell zugreifen, dieser verfügt jedoch über eine relativ kleine Speicherkapazität. Viel mehr Platz ist auf der Festplatte vorhanden. Dort benötigen Zugriffe jedoch deutlich mehr Zeit. Die Zugriffszeiten stehen dabei in einem Verhältnis von ca. 1:106. Würde ein Hauptspeicherzugriff 1 Sekunde dauern, so müsste man auf die gleichen Daten von der Festplatte etwa 11,5 Tage warten. Aus diesem Grund benötigen wir einen Algorithmus, der Seiten derart in den Hauptspeicher lädt und aus ihm entfernt, dass wir möglichst selten auf die Festplatte zugreifen müssen. In dem folgenden Beispiel sind gerade die Speicherseiten A, B, C, D, E und G im Hauptspeicher. Der Prozessor erzeugt zunächst Datenanfragen auf die Seiten D, B, A, C, D, E, G und ist in der glücklichen Lage, alle Seiten im schnellen Hauptspeicher vorzufinden.
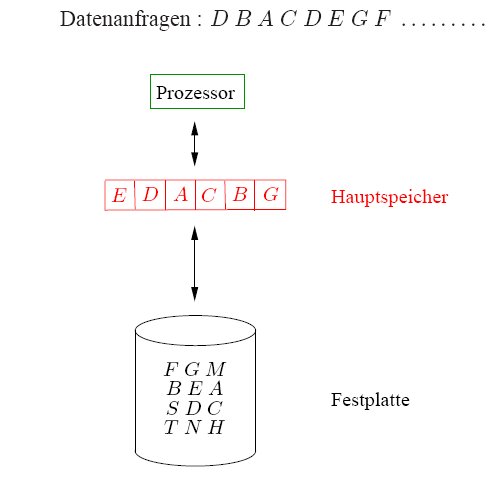
Bei der nächsten Anfrage haben wir jedoch Pech. Die benötigte Seite F liegt auf der Festplatte! Dieses Ereignis nennt man einen Seitenfehler. Jetzt muss die fehlende Seite von der Platte in den Hauptspeicher geladen werden. Leider ist dieser voll, und wir sind gezwungen, eine Seite zu entfernen, um die fehlende Seite in den Hauptspeicher zu bringen und den Datenzugriff durchzuführen. Aber welche Seite soll entfernt werden? Hier entsteht ein Online-Problem: Bei einem Seitenfehler muss ein Seitenwechsel-Algorithmus entscheiden, welche Seite aus dem Hauptspeicher auszulagern ist, ohne zukünftige Datenanfragen zu kennen. Wüsste man, welche Seite im Hauptspeicher lange nicht benötigt wird, so könnte man sich von dieser trennen. Dies ist aber nicht bekannt. Die folgende Online-Strategie hat sich in der Praxis bewährt.
In unserem Beispiel würde LRU die Seite B entfernen, da auf diese die längste Zeit nicht zugegriffen wurde. Die Intuition von LRU ist, dass lange nicht benötigte Seiten für den Prozessor offenbar nicht mehr so interessant sind und somit hoffentlich auch in der nahen Zukunft nicht gebraucht werden. Man kann zeigen, dass LRU k-kompetitiv ist, wobei k die Anzahl der Seiten ist, die gleichzeitig im Hauptspeicher gehalten werden kann. Dies ist durchaus eine hohe Kompetitivität, denn in der Praxis ist k groß. Andererseits zeigt das Ergebnis, dass LRU eine beweisbare Güte besitzt. Dies trifft auf viele andere Seitenwechsel-Strategien nicht zu.
Neben LRU gibt es noch andere Strategien, die versuchen das Seitenwechselproblem möglichst gut zu lösen.
Für MRU kann man eine Sequenz von Anfragen konstruieren, die bei vollem Hauptspeicher in jedem Schritt einen Seitenfehler erzeugt. Dazu fragt man bei vollem Hauptspeicher zwei Seiten A und B, die nicht im Hauptspeicher sind, immer wieder wechselseitig an. Bei der ersten Anfrage an A wird die Seite A in den Hauptspeicher geladen, nachdem gemäß MRU eine Seite entfernt wurde. Wird nun B angefragt, so wird A aus dem Hauptspeicher entfernt, da diese Seite zuletzt angefragt wurde. Jetzt wird wieder die Seite A angefragt. Da wir A gerade entfernt haben, müssen wir sie erneut von der Festplatte in den Hauptspeicher laden und B gemäß MRU wieder entfernen. Dann wird wieder B angefragt usw. Wie wir sehen, erzeugt unsere Online-Strategie MRU in jedem Schritt einen Seitenfehler. Der optimale Algorithmus lädt die beiden Seiten A und B bei der jeweils ersten Anfrage in den Hauptspeicher und behält sie dann dort. Er erzeugt also nur zwei Seitenfehler. Unsere Online-Strategie MRU ist für diese Anfragesequenz also sehr schlecht. Das zwei oder wenige Seiten zyklisch angefragt werden, ist in der Praxis häufig anzutreffen, da in Programmen oft Schleifen auftreten, die auf wenige Speicherseiten zugreifen. Die Strategie MRU sollte daher in der Praxis nicht angewandt werden.
In der Informatik treten in sehr vielen Bereichen Online-Probleme auf. Beispiele sind die Datenstrukturierung, das Prozessorscheduling oder die Robotik, um nur einige Gebiete zu nennen.
- Paging (Seitenwechselproblem) (Wikipedia)

