 Rolf Wanka, FAU Erlangen-Nürnberg
Rolf Wanka, FAU Erlangen-Nürnberg
 Seit es Hardware gibt, überlegt man sich, spezielle Geräte
zu bauen, die ganz besonders schnell die bereits mehrfach im Rahmen des
Algorithmus der Woche (ganz besonders im
3.
Algorithmus der Woche: Schnelle Sortieralgorithmen) angesprochene
Sortieraufgabe lösen können.
Seit es Hardware gibt, überlegt man sich, spezielle Geräte
zu bauen, die ganz besonders schnell die bereits mehrfach im Rahmen des
Algorithmus der Woche (ganz besonders im
3.
Algorithmus der Woche: Schnelle Sortieralgorithmen) angesprochene
Sortieraufgabe lösen können.
Schon als Herman Hollerith um 1890 seine berühmte Hollerith-Maschine zur Auswertung der amerikanischen Volkszählung baute, hatte er ein zusätzliches Gerät zum Sortieren der Lochkarten konstruiert. In der Abbildung links ist eine solche Hollerith-Maschine im Original zu sehen. Das rechte, etwas kleinere Gerät ist dabei die Lochkarten-Sortiereinheit. Im Zeitalter der Elektronik im Miniaturformat muss ein solcher Sortierer natürlich sehr viel kleiner ausfallen als Holleriths Gerät.
Wir werden im Folgenden eine Konstruktionsvorschrift für einen Hardware-Sortierer angeben. Dieser Sortierer bekommt gleichzeitig auf n Leitungen eine beliebig wirre Folge aus n Zahlen, die er sortieren soll. Dieser Sortierer soll nur aus ganz bestimmten Bausteinen zusammengesetzt werden, die Komparatoren genannt werden. Ein solcher Komparator hat zwei Eingänge e[1] und e[2] und zwei Ausgänge x[1] und x[2]. Zwei beliebige natürliche Zahlen a und b kommen nun über die Eingangsleitungen in den Komparator hinein. Als Ausgabe wird über die Ausgangsleitung x[1] die kleinere der beiden Zahlen zurückgegeben, also x[1]=min{a,b}, und über x[2] die größere der beiden, also x[2]=max{a,b}. Die folgende Abbildung zeigt zwei Möglichkeiten, einen solchen Komparator zu zeichnen. Wir werden die rechte, kompaktere Darstellung nutzen. Um das elektronische Innenleben eines Komparators wollen wir uns hier auch gar nicht kümmern.

Die Eingabe a=7 und b=4 wird also von einem Komparator wie folgt weitergeleitet:

Haben wir nur einen einzigen Komparator zur Verfügung, so können wir ihn einsetzen, um mit ihm in den bereits vorgestellten Verfahren wie Mergesort und Quicksort die dort benutzten bedingten Vertauschungen durchzuführen. Da wir aber nur einen Komparator haben, muss er nacheinander, d.h. sequentiell die notwendigen bedingten Vertauschungen abarbeiten.
Wir wollen nun mit vielen Exemplaren dieses Bausteins eine Schaltung konstruieren, die Zahlenfolgen der Länge n schneller als die sequentiellen Verfahren sortiert.
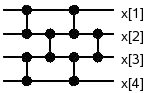 Mit einem Beispiel wollen wir beginnen. Schau Dir das Bild links an. Die
Eingabe kommt von links und läuft nach rechts durch die Schaltung durch.
Statt Schaltung sagt man auch gerne Netzwerk. Eine einfache Überlegung
zeigt, dass dieses Netzwerk aus 6 Komparatoren jede Zahlenfolge der Länge 4 zu
sortieren vermag: Egal, auf welcher Leitung wir links die kleinste Zahl
eingeben, sie verlässt immer auf der obersten Leitung rechts das Netzwerk. Für
die größte Zahl gilt entsprechend, dass sie unabhängig davon, wo sie das
Netzwerk betritt, auf der untersten Leitung das Netzwerk verlässt. Und wie wir
auch sehen, wird zum Schluss durch den letzten Komparator gerade dafür gesorgt,
dass x[2] ≤ x[3] ist. Wir erkennen also, dass dieses Netzwerk
jede Eingabefolge sortiert. Darum wird es auch Sortiernetzwerk
genannt.
Mit einem Beispiel wollen wir beginnen. Schau Dir das Bild links an. Die
Eingabe kommt von links und läuft nach rechts durch die Schaltung durch.
Statt Schaltung sagt man auch gerne Netzwerk. Eine einfache Überlegung
zeigt, dass dieses Netzwerk aus 6 Komparatoren jede Zahlenfolge der Länge 4 zu
sortieren vermag: Egal, auf welcher Leitung wir links die kleinste Zahl
eingeben, sie verlässt immer auf der obersten Leitung rechts das Netzwerk. Für
die größte Zahl gilt entsprechend, dass sie unabhängig davon, wo sie das
Netzwerk betritt, auf der untersten Leitung das Netzwerk verlässt. Und wie wir
auch sehen, wird zum Schluss durch den letzten Komparator gerade dafür gesorgt,
dass x[2] ≤ x[3] ist. Wir erkennen also, dass dieses Netzwerk
jede Eingabefolge sortiert. Darum wird es auch Sortiernetzwerk
genannt.
Am Beispiel sieht das so aus:

Eine weitere interessante Beobachtung können wir der Zeichnung auch noch entnehmen: Alle untereinander stehenden Komparatoren können gleichzeitig ausgeführt werden. Es vergehen also nur 4 Zeiteinheiten, bis die Eingabe sortiert vom Netzwerk ausgegeben wird. Statt von Zeiteinheiten spricht man auch von parallelen Schritten.
Können wir nun die bereits vorgestellten, schnellen sequentiellen (nicht parallelen) Verfahren wie z.B. Quicksort und Mergesort, die als Grundoperation ja auch die Funktionsweise des Komparators benutzen, durch Netzwerke aus Komparatoren realisieren? Leider ist das nicht direkt möglich, da man bei ihnen zu Beginn nie weiß, auf welchen Indexpositionen irgendwann später ein Komparator angewandt werden muss. Denn das hängt bei den schnellen sequentiellen Verfahren von der Eingabe, oder genauer, davon, wie frühere Vergleiche ausgegangen sind, ab! Bei einem Komparator-Netzwerk kann das nicht der Fall sein, hier haben wir uns schon vor dem Start festgelegt, zwischen welchen Leitungen Komparatoren sind.
Deswegen hat Kenneth Batcher, ein Wissenschaftler aus den USA, 1968 ein
spezielles Netzwerk konstruiert, das in wenigen, nämlich
Wir wollen also nun n Zahlen sortieren. Dazu konstruieren wir das Sortiernetzwerk Sn. Weil wir mit der Teile-und-Herrsche-Methode die Anzahl der Zahlen immer wieder in zwei gleichgroße Teile zerlegen werden, wählen wir der Einfachheit halber n=2k, da wir dann immer wieder ohne Rest durch 2 dividieren können. Angenommen, wir wüssten schon, wie wir halb so viele, also n/2=2k-1 Zahlen mit Hilfe eines Netzwerks Sn/2 sortieren könnten. Dann sortieren wir mit zwei Kopien von Sn/2 gleichzeitig erst einmal die obere und die untere Hälfte der Eingabe. Dies ist der Teile-Schritt des Teilens und Herrschens.
Jetzt bleibt als Herrsche-Schritt wie im 3. Algorithmus der Woche die Aufgabe
des Mischens zu lösen, d.h. nun müssen wir ein Netzwerk aus
Komparatoren angeben, das aus zwei sortierten Zahlenfolgen
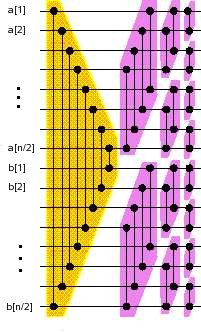
Es beginnt immer mit dem gelb unterlegten Schritt (das ist wirklich nur ein einziger Schritt, die Komparatoren sind nur nebeneinander gezeichnet, um sie besser erkennen zu können) und führt danach die violett unterlegten Schritte aus. Das Muster dieser beiden Schrittarten ist für uns hier und heute klar und braucht nicht mehr extra beschrieben zu werden.
Wer den Beweis überspringen möchte, klickt hier.
Dass dieses Netzwerk die beiden sortierten Folgen a und b in eine sortierte Gesamtfolge verwandelt, ist bei weitem nicht offensichtlich. Um das zu beweisen, nutzen wir eine tolle Eigenschaft der Komparator-Netzwerke, das sog. 0-1-Prinzip:
- Sortiert das
Komparator-Netzwerk jede Folge der Länge n, die nur aus 0-en und 1-en
besteht, so sortiert es auch jede beliebige Zahlenfolge der Länge n.
Ab jetzt betrachten wir also erst einmal nur noch 0-1-Folgen. Nun sind wir soweit, dass wir zeigen können, dass der Bitone Mischer aus den sortierten 0-1-Folgen a und b eine sortierte Gesamtfolge macht. Und hier kommt nun der Begriff biton ins Spiel. Bitone Folgen entstehen, indem eine monoton steigende 0-1-Folge x (das ist eine Folge, bei der die einzelnen Zahlen von links nach rechts größer werden oder gleich bleiben, aber niemals kleiner werden) und eine monoton fallende 0-1-Folge y (das ist eine Folge, bei der die einzelnen Zahlen von links nach rechts kleiner werden oder gleich bleiben, aber niemals größer werden) beliebig herum aneinander geklebt werden, d.h. xy und yx sind biton. Und daher kommt dann auch der Name: Zweimal (bi) monoton (ton).
Klingt kompliziert? Ist es aber nicht, wenn Du Dir ein paar Beispiele ansiehst: 00111000, 11100011, 0000, 11111000 und 11111111 sind alles bitone Folgen. Sicher findest Du die notwendigen Folgen x und y, oder? Es gibt jedesmal ganz viele.
Was macht nun der gelbe Schritt, also der erste Schritt des Bitonen Mischers? Drehen wir die Folge b einfach mal um und schreiben a und b untereinander. Dann entsteht zum Beispiel das folgende Bild.
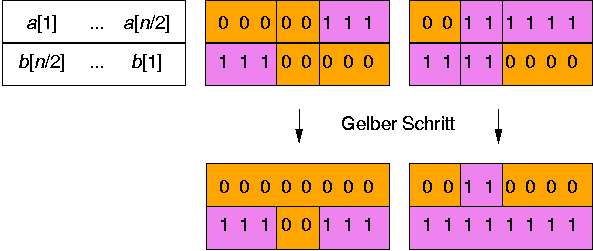
Auf untereinander stehende Zahlen werden die Komparatoren des gelben Schrittes angewandt, d.h. die kleinere der beiden Zahlen wird nachher oben, die größere unten stehen. Die beiden farbigen Teile zeigen zwei Beispiele. Nach Anwendung des gelben Schrittes ist immer eine ganze Hälfte, und zwar die richtige, voller 0-en bzw. voller 1-en, und die andere Hälfte ist biton! Diese Hälfte ist jetzt die Eingabe der violetten Schritte. Schneide einmal eine bitone 0-1-Folge in der Mitte durch und schreibe die Hälften untereinander. Es entsteht das gleiche Bild wie gerade, und wieder werden auf untereinander stehende Zahlen die Komparatoren des nächsten Schrittes angewandt. Versuche doch mal selbst ein paar Beispiele. Zum Schluss, nach dem letzten violetten Schritt, muss die ganze 0-1-Folge also auch sortiert sein.
(Wer den Beweis übersprungen hat, kann ab hier
weiterlesen.)
So, und nun können wir uns überlegen, wie Sn/2
aussieht. Auch Sn/2 endet mit einem Bitonen Mischer,
diesmal nur für n/2 viele Eingangsleitungen. Gespeist wird dieser
Bitone Mischer von zwei Kopien von Sn/4. Das
wiederholt sich, bis der die einspeisenden Sortierer nur noch zwei Zahlen zu
sortieren haben, wofür wir dann einfach einen Komparator nehmen.
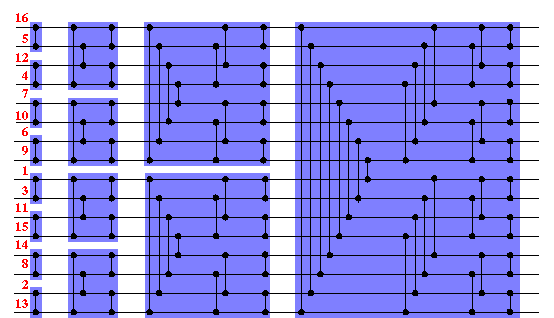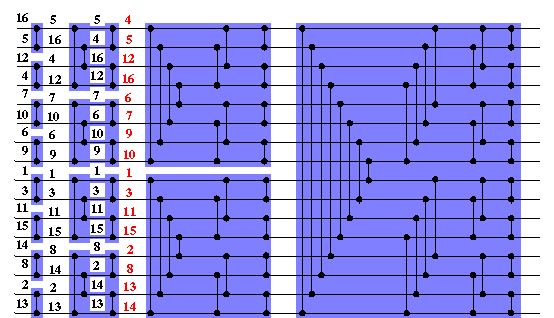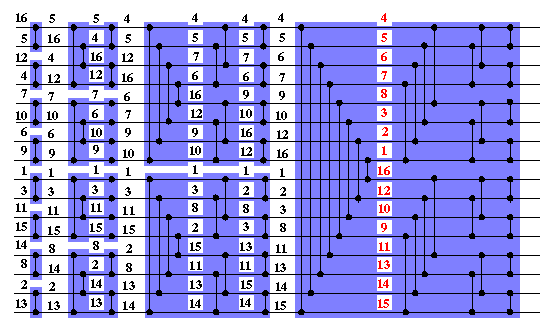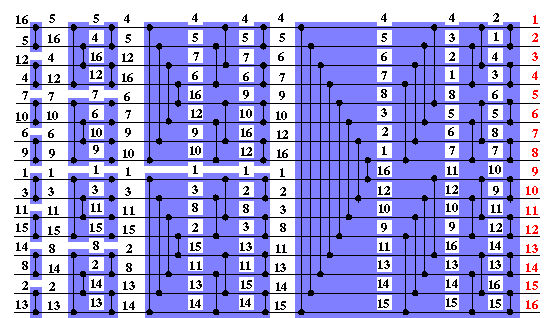
Insgesamt bekommen wir also z.B. das nachfolgend dargestellte Gesamtnetzwerk
S16, das jede 0-1-Folge der Länge 16 und damit, wegen
des 0-1-Prinzips, auch jede Folge aus 16 Zahlen in 10 parallelen Schritten
sortiert! Dabei ist jeder blau unterlegte Kasten ein Bitoner Mischer. Das
gesamte Netzwerk heißt dann Bitoner Sortierer.
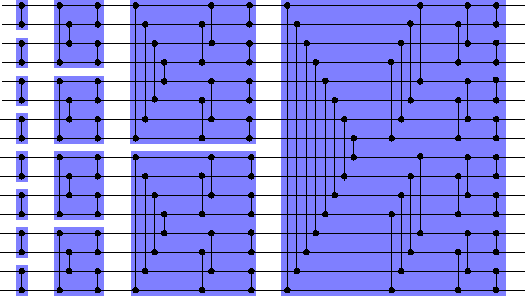
Hier ist noch ein kleines Beispiel, in dem 16 Zahlen von S16 sortiert werden.
- Friedhelm Meyer auf der Heide, Rolf Wanka. Von der Hollerith-Maschine zum Parallelrechner. Die alltägliche Aufgabe des Sortierens als Fortschrittsmotor für die Informatik. ForschungsForum Paderborn (FFP) 3 (2000) 112-116.
- 3. Algorithmus der Woche: Schnelle Sortieralgorithmen von Helmut Alt.
- Kenneth E. Batcher. Sorting networks and their applications. In AFIPS Conf. Proc. 32, 307-314, 1968.

