Algorithmus der Woche

• » Startseite
• » aktueller Algorithmus
• » Liste der Algorithmen

Informationen

• » Infoflyer Presse
• » Infoflyer Schule
• » Download Logo

Gimmicks für's Klassenzimmer

• » Visuelle Kryptographie

Links

• » Informatikjahr
• » Fakultätentag Informatik

Intern

• » Für Autoren
• » Für Organisatoren
• » Buchprojekt

Sonstiges

• » Impressum
• » Gästebuch
• » Haftung

Unser heutiges Ziel besteht darin, Kartenspiele, beispielweise Poker, zu spielen, ohne dass sich die Spieler dazu treffen müssen. Stattdessen soll das Mischen und Verteilen der Karten über das Internet erfolgen. Die einfachste Möglichkeit besteht darin, kommerzielle Online-Poker-Systeme zu benutzen, die das Mischen und Verteilen der Karten übernehmen. Wir wollen hier aber eine andere Frage behandeln, nämlich, ob die Spieler auch ohne einen vertrauenswürdigen Kartengeber fair miteinander spielen können. Die Spieler sollen also selbst das Mischen und Verteilen der Karten übernehmen. Dabei treten eine Reihe von offensichtlichen Schwierigkeiten auf: Wenn ein Spieler das Mischen und Geben übernimmt, muss er dies tun, ohne etwas über die Karten zu erfahren, die er verteilt. Er muss dazu E-Mails an die anderen Spieler senden, aus denen diese ihre Karten entnehmen können, der Kartengeber aber nicht. Weiterhin darf kein Spieler wissen, welche Karten bereits vergeben wurden, andererseits muss aber sichergestellt werden, dass Karten nicht mehrfach vergeben werden. Schließlich wollen die beteiligten Spieler sicher sein, dass ihre Gegenspieler fair spielen, d.h., es darf nicht möglich sein zu mogeln, ohne dass dies auffällt.

Pokern mit Briefpost

Um Ideen zu sammeln, wie man Kartenspiele per E-Mail realisieren kann, überlegen wir zunächst, ob und wie dies mit normaler Briefpost gehen kann. Wir betrachten nur die Situation mit zwei Spielern Alice und Bob. Diese halten sich an verschiedenen Orten auf und können somit nicht beobachten, was ihr Gegenspieler macht.

Die einfachste Möglichkeit für einen Spieler zu mogeln besteht darin, Karten aus einem zweiten identischen Kartenspiel ins Spiel zu bringen. Er könnte sich dann bei Bedarf immer gute Karten, beispielsweise einen Royal Flush, aus dem zweiten Kartenspiel auswählen. Um sicherzustellen, dass dies nicht passiert, wird ein Kartenspiel verwendet, bei dem jede Karte ein eindeutiges Siegel hat, mit dem sie sich von Karten aus anderen Kartenspielen unterscheidet.

Mischen und Verteilen der Karten

Beim Pokern verwenden wir ein Kartenspiel mit den 52 Karten Kreuz-As, Kreuz-Zwei, ..., Karo-König. Nach dem Mischen soll jeder Spieler fünf Karten erhalten. Wie kann ein Spieler die Karten mischen und verteilen, ohne dass er dabei die Möglichkeit hat, die Karten zu sehen? Wir verwenden dazu Briefumschläge. Bob packt jede der 52 Karten in einen z.B. gelben Umschlag. Damit später klar ist, wer die Karte in den Umschlag gesteckt hat, versieht er jeden Umschlag mit seiner Unterschrift.

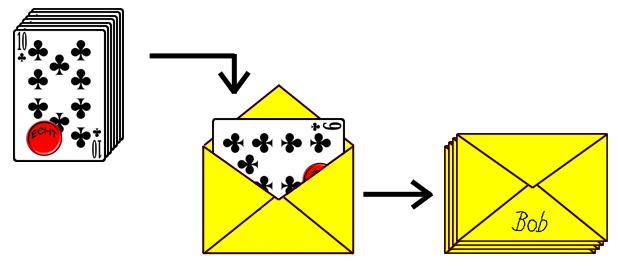
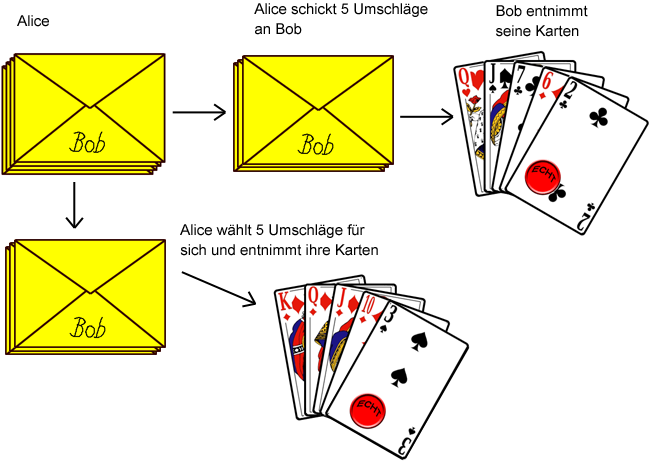
Dann mischt er den Stapel von 52 Umschlägen und schickt ihn an Alice. Für Alice sehen die Umschläge alle gleich aus, sodass sie nicht in der Lage ist, für sich selbst bessere Karten und für Bob schlechtere Karten auszuwählen. Also kann Alice nur die Umschläge mischen und für sich selbst und für Bob jeweils fünf Umschläge auswählen. Dies entspricht einer zufälligen Auswahl der Karten. Alice sendet Bob seine fünf Umschläge zu, und er kann seine Karten einfach entnehmen. Ebenso kann Alice ihre fünf Karten entnehmen.

Sind die Karten wirklich fair gemischt worden?

Welche Möglichkeiten gibt es hier zu mogeln? Alice könnte beispielsweise weitere Umschläge öffnen, um aus dieser größeren Menge von Karten die besten Karten auszusuchen. Dies kann man zu diesem Zeitpunkt offensichtlich nicht verhindern. Wenn Alice aber fair gespielt hat, kann sie nach Ende des Spiels, z.B., wenn sich Alice und Bob später einmal treffen, 42 geschlossene und von Bob unterschriebene Umschläge vorweisen. Da die Umschläge von Bob unterschrieben wurden, kann sie auch eine einmal entnommene Karte nicht wieder verpacken, ohne dass dies auffällt. Wenn Bob beim Verpacken der Karten einen Fehler gemacht hat, beispielsweise eine Karte behalten hat und dafür einen Umschlag leer gelassen hat, kann er ebenfalls keinen Vorteil daraus ziehen. Wenn er den leeren Umschlag während des Spiels zieht, hätte er sowieso die nicht verpackte Karte bekommen. Anderenfalls fällt spätestens bei der Kontrolle der Umschläge auf, dass er beim Verpacken der Karten einen Fehler gemacht hat.

Bieten

Nach dem Verteilen der Karten, kommt beim Pokern das Bieten. Jeder Spieler kann einen Geldbetrag setzen oder erhöhen oder kann auch passen. Was beim normalen Pokern mündlich gemacht wird, kann man ohne weitere Ideen auch schriftlich durchführen, d.h., die Spieler teilen sich ihre Entscheidungen einfach in Briefen mit.

Tauschen von Karten

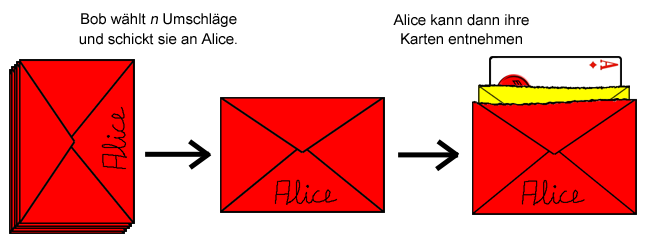
Nach dem Bieten darf jeder Spieler eine oder mehrere seiner Karten tauschen. Zuerst kann Alice n Karten tauschen (wobei n zwischen 1 und 5 liegt). Hierbei gibt es aber eine Komplikation: Alice muss zuerst n Karten weglegen und darf dann erst n neue Karten erhalten. Wenn sie sich selber die neuen Karten auf die oben beschriebene Weise gibt, kann man nicht mehr feststellen, ob sie nicht zuerst n neue Karten genommen hat und dann erst die Karten ausgewählt hat, die sie angeblich schon zuvor weggelegt hat. Also muss Bob an der Verteilung von weiteren Karten an Alice beteiligt werden.

Andererseits darf Alice die 42 vorhandenen Umschläge nicht einfach an Bob zurücksenden. Damit verliert sie ihren Beweis, dass sie bis jetzt fair gespielt hat. Weiterhin könnte Bob geheime Markierungen an den gelben Umschlägen angebracht haben, mit Hilfe derer er die guten Karten erkennt, beispielsweise durch geringfügige Unterschiede in seinen Unterschriften. Dies geht auch noch unauffälliger als in dem folgenden Bild, in dem das kleine "b" je nach Inhalt etwas anders geschrieben ist.

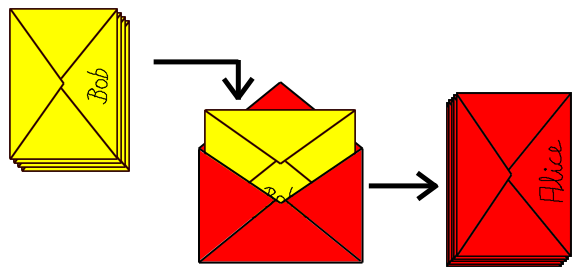
Der Trick mit Umschlägen funktioniert aber auch hier. Alice verpackt die verbliebenen 42 gelben Umschläge in etwas größere rote Umschläge, unterschreibt diese, mischt den Stapel und sendet die Umschläge an Bob.

Weiterhin verpackt sie die n Karten, die sie tauschen möchte, in einem separaten Umschlag und schickt diesen ebenfalls an Bob. Den Umschlag mit den weggelegten Karten lässt er ungeöffnet, da er nicht erfahren darf, welche Karten Alice weggelegt hat. Später kann dann leicht überprüft werden, ob dieser Umschlag verschlossen geblieben ist und tatsächlich n Karten enthält.

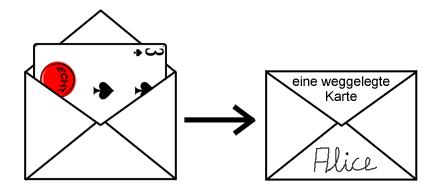
Da für Bob die roten Umschläge alle gleich aussehen, kann er nichts Besseres machen, als die Umschläge ebenfalls zu mischen und dann n rote Umschläge auszuwählen. Diese schickt er an Alice, die damit die ausgetauschten Karten erhält.

Wenn Bob Karten tauschen möchte, geht dies nach demselben Schema, wobei Bob die roten Umschläge in eine weitere Schicht von Umschlägen verpackt.

Aufdecken der Karten

Das Pokerspiel endet mit dem Aufdecken der Karten. Jeder der Spieler teilt dem anderen nur mit, welche Karten er hat. Die Karten behält jeder Spieler, um bei Bedarf bei einem späteren Treffen nachweisen zu können, dass er diese Karten wirklich hat. Damit steht der Gewinner fest.

Kontrolle, ob fair gespielt wurde

Das bisher beschriebene Verfahren bietet beiden Spielern viele Möglichkeiten, durch abweichendes Verhalten einen Vorteil zu erlangen. Beispielsweise könnte ein Spieler Umschläge öffnen, die er nicht öffnen darf, um eine größere Auswahl an Karten oder Informationen über die Karten des Gegners zu erhalten. Dies lässt sich aber einfach entdecken: Die Karten und die ungeöffneten Umschläge werden bis zum nächsten Treffen von Alice und Bob aufbewahrt. Dann können beide die Karten vorweisen und die Umschläge gemeinsam öffnen, um zu überprüfen, ob der andere sich an das beschriebene Verfahren gehalten hat, also fair gespielt hat.

Diskussion

Das Pokern mit normaler Post hat mehrere offensichtliche Nachteile:

• Das Verpacken in Umschläge ist nur von Hand möglich und recht aufwendig. Die gebrauchten Umschläge können nicht wiederverwendet werden.
  
• Die Überprüfung, ob der andere Spieler fair gespielt hat, kann erst bei dem nächsten Treffen der beiden durchgeführt werden. Für jedes weitere Spiel vor diesem Treffen wird also ein weiteres Kartenspiel mit einem jeweils anderen Siegel benötigt.
  
• Die normale Post ist zu langsam, sodass das Spiel nicht viel Spaß macht, und im Vergleich zu E-Mail auch teuer.
• Wenn ein Brief abhanden kommt, kann man das Spiel nicht zu Ende spielen. Wenn ein Spieler merkt, dass er verliert, könnte er sogar einen Brief verschwinden lassen, und es ist später nicht mehr feststellbar, wer Schuld daran ist.
  

Die naheliegende Frage ist nun, ob man "elektronische Briefumschläge" realisieren kann, die ähnliche oder vielleicht sogar bessere Eigenschaften als die Briefumschläge aus Papier haben. Insbesondere sollte man sie mit Hilfe eines Computers erzeugen und per E-Mail verschicken können. Man spart dann die Arbeit, die Karten einzeln von Hand zu verpacken, und verloren gegangene E-Mails kann man ein zweites Mal verschicken.

Pokern mit elektronischer Post

Elektronische Umschläge

Wie können die Umschläge mit elektronischer Post realisiert werden? Eine Idee besteht darin, dass Bob die Karten codiert und Alice beim Mischen nur die Codes sieht. Dabei soll Alice keine Idee haben, welcher tatsächlichen Karte ein Code entspricht. Bevor wir allgemein beschreiben, wie das Mischen und Verteilen der Karten realisiert werden kann, konzentrieren wir uns auf den Spezialfall, dass Karten nur an Bob auszugeben sind. Wir gehen im Folgenden an manchen Stellen davon aus, dass die Karten feste Nummern zugeordnet bekommen haben und beide Spieler diese Zuordnung kennen, also 0 entspricht dem Kreuz-As, 1 der Kreuz-Zwei, 2 der Kreuz-3, ..., 12 dem Kreuz-König, 13 dem Pik-As usw. bis 51 dem Karo-König.

Mischen und Ausgabe der Karten an Bob

Bob erzeugt zu Beginn zufällige Codes für die Karten, d.h., eine Tabelle der folgenden Form:

Karte	Code
0   (Kreuz-As)	1
1   (Kreuz-Zwei)	42
2   (Kreuz-Drei)	22
3   (Kreuz-Vier)	25
4   (Kreuz-Fünf)	51
5   (Kreuz-Sechs)	0
6   (Kreuz-Sieben)	43
…
51 (Karo-König)	13

In der linken Spalte der Tabelle sind alle Karten aufgeführt. Die rechte Spalte wurde zufällig erzeugt, sodass jeder Code aus dem Bereich von 0 bis 51 genau einmal vorkommt. Alice soll diese Tabelle zunächst nicht erhalten.

Um fünf Karten für Bob auszuwählen, wählt Alice zufällig fünf Codes aus dem Bereich von 0 bis 51 aus und sendet sie an Bob. Der benutzt dann die Tabelle, um herauszufinden, welche Karten er bekommen hat. Wenn Alice beispielsweise die Codes 0, 1, 13, 42 und 51 ausgewählt hat, erhält Bob gemäß der Tabelle oben die Karten Kreuz-Sechs, Kreuz-As, Karo-König, Kreuz-Zwei und Kreuz-Fünf. Da Alice die Tabelle nicht kennt, kann sie keinen Einfluss darauf nehmen, welche Karten Bob bekommt. Weiterhin kann sie sich merken, welche Codes bereits gebraucht wurden, sodass sie sicherstellen kann, dass jede Karte nur einmal ausgegeben wird.

Die Vorgehensweise ist also ähnlich zu den Briefumschlägen. Anstatt das Kreuz-As in einen gelben Briefumschlag zu verpacken, erhält es von Bob einen Code, im betrachteten Beispiel die Nummer 1. Bei der Verwendung von Briefumschlägen kann Alice nicht in den Umschlag hineinsehen. Hier kennt Alice die Bedeutung des Codes 1 nicht. Somit kann Alice in beiden Fällen beim Mischen und Geben der Karten keinen Einfluss auf die gewählten Karten nehmen.

Allerdings könnte Bob am Ende des Spiels behaupten, dass er eine ganz andere Tabelle erzeugt hat, und sich somit nachträglich bessere Karten geben. Also muss sich Bob zu Beginn in einer für Alice nachprüfbaren Weise auf eine Tabelle festlegen, sodass er sie im Nachhinein nicht mehr verändern kann. Wir verwenden dazu die sogenannten Einwegfunktionen.

Einwegfunktionen

Einwegfunktionen wurden bereits im 17. Algorithmus der Woche ausführlich vorgestellt. Wir erinnern uns: Eine Einwegfunktion f  ist eine Funktion, die leicht berechnet werden kann, bei der aber die Umkehrfunktion f ^-1 schwer zu berechnen ist. Ein Beispiel im Beitrag über Einwegfunktionen war ein Telefonbuch: Die Einwegfunktion f entspricht dem Finden einer Telefonnummer zu einem gegebenen Namen, was leicht ist. Die Umkehrfunktion f ^-1 entspricht dem Finden des Namens zu einer Telefonnummer, was dagegen schwer ist.

Wie können wir jetzt Einwegfunktionen nutzen, damit Bob die Tabelle der Codierungen der Karten nachträglich nicht mehr ändern kann? Wir stellen uns dazu in Analogie zu dem Telefonbuch vor, dass Alice und Bob ein Buch mit sehr vielen Codierungstabellen bekommen haben, das zu jeder aufgeführten Codierungstabelle eine eindeutige Zahl angibt.


Die Ausgabe der Karten an Bob erfolgt dann so: Zuerst wählt Bob zufällig eine Codierungstabelle  aus dem Buch (z.B. die untere auf Seite 569)  und sendet die zugehörige eindeutige Zahl an Alice. Im Beispiel ist dies 039784. Wenn Alice erfahren möchte, welche Codierungstabelle Bob benutzt, muss sie im Wesentlichen das gesamte Buch durchlesen. Wenn dies für sie zu aufwendig ist, hat sie keine Möglichkeit, die verwendete Codierungstabelle zu finden. Sie kann also nichts Besseres tun, als zufällig fünf Zahlen aus dem Bereich von 0 bis 51 auszuwählen und an Bob zu senden. Der erhält dann anhand der verwendeten Tabelle seine Karten. Der Karte mit der Nummer 0 (also dem Kreuz-As) wird also der Code 1 zugeordnet, der Karte mit der Nummer 1 (also der Kreuz-Zwei) der Code 42, usw. Nach Ende des Spiels kann Bob angeben, wo in dem Buch die verwendete Tabelle steht. Somit erhält Alice die Tabelle und kann nachsehen, ob die Nummer dieser Tabelle mit der zu Beginn von Bob genannten Nummer übereinstimmt und ob Bob wirklich die Karten bekommen hat, von denen er dies behauptet.

Tauschen von Karten

Das Weglegen von Karten erfordert nun keine neuen Ideen. Wenn Bob im obigen Beispiel die Kreuz-Zwei weglegen will, teilt er Alice einfach mit, dass er die Karte mit dem Code 42 weglegen möchte. Da Alice den Zusammenhang zwischen Kreuz-Zwei und dem Code 42 nicht kennt, erfährt sie auch nicht, welche Karte Bob weggelegt hat. Anschließend kann Alice Bob neue Karten geben. Da sie weiß, welche Codes sie bereits an Bob gesendet hat, kann sie auch verhindern, Karten mehrfach zu geben, ohne zu wissen, welche Karten sie bereits ausgegeben hat.

Mathematischere Formulierung

Etwas mathematischer formuliert, beschreibt das Buch mit den Codierungstabellen eine Einwegfunktion. Diese Einwegfunktion f  bildet die Position der Codierungstabellen auf Zahlen ab. In dem beschriebenen Verfahren wählt Bob zufällig eine Codierungstabelle mit der Position x im Buch und sendet f (x) an Alice. Da f eine Einwegfunktion ist, kann Alice nicht auf effiziente Weise x aus f (x) berechnen; dies würde dem Durchsuchen des Buchs entsprechen. Nach Ende des Spiels kann Bob ihr x zusenden. Alice kann dann leicht f (x) berechnen und überprüfen, ob dies wirklich der Wert ist, den sie zu Beginn erhalten hat. Somit kann Bob nicht nachträglich behaupten, eine andere Codierungstabelle verwendet zu haben.

Für einen Computer ist es nun kein Problem, ein komplettes Buch zu speichern und zu durchsuchen. Statt eines solchen Buches sollte man daher Einwegfunktionen verwenden, die aus der Codierungstabelle direkt die Zahl ausrechnen, mit der sich die Spieler auf die verwendete Tabelle festlegen. Auf die Einzelheiten dazu wollen wir hier aber nicht eingehen.

Man kann auch jede Codierungstabelle selbst als Funktion auffassen. Wir verwenden dazu die festen Nummern der Karten, die wir bereits oben in der Tabelle angegeben haben. Die Codierungstabelle ist dann eine Funktion b, die den Nummern der Karten (die aus dem Bereich von 0 bis 51 sind) Codierungen zuordnet (in unserem Beispiel ebenfalls aus dem Bereich von 0 bis 51). Anhand der Codierungstabelle können wir auch leicht die Umkehrfunktion b^-1 von b berechnen. Die Funktion b^-1 ordnet jedem Code die Nummer der zugehörigen Karte zu. Um b^-1(z) zu berechnen, suchen wir den Eintrag z in der rechten Spalte der Tabelle und lesen das Ergebnis in der linken Spalte ab. Da in der rechten Spalte der Tabelle jede Zahl genau einmal vorkommt, gilt für alle x, dass b^-1(b(x))=x ist.

Verteilen von Karten an beide Spieler

Um Karten an beide Spieler ausgeben zu können, benutzen Alice und Bob eigene Codierungstabellen, die sie unabhängig voneinander erzeugen und dem Gegenspieler jeweils nicht bekannt geben. Die Funktion, die von Alice' Codierungstabelle beschrieben wird, bezeichnen wir mit a, die von Bobs Codierungstabelle mit b. Als weitere Voraussetzung an a und b verlangen wir, dass für alle x aus dem Bereich von 0 bis 51 gilt, dass a(b(x))=b(a(x)) ist. Die Mathematiker sagen auch dazu, dass die Funktionen a und b kommutieren, d.h., dass wir unabhängig davon, ob wir zuerst b und dann a auf x anwenden oder umgekehrt, denselben Funktionswert erhalten.

Ein Beispiel für kommutierende Funktionen sind die Folgenden:

   

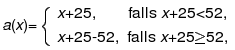
        und

   

Wir haben hier die Codierungstabellen nicht vollständig aufgeschrieben, sondern nur auf mathematische Weise beschrieben, wie man zu einem Eintrag in der linken Spalte den zugehörigen Eintrag in der rechten Spalte findet. Man rechnet leicht nach, dass a(b(x)) und b(a(x)) überstimmen: Für die Berechnung von a(b(x)) addiert man zu x zunächst die 37 und anschließend die 25, wobei man jeweils 52 abzieht, falls das Ergebnis größer als 51 wird, für die Berechnung von b(a(x)) führt man diese Additionen einfach in der umgekehrten Reihenfolge aus. Statt der 37 und der 25 kann man auch andere Zahlen nehmen.

Dieses anschauliche Beispiel von kommutierenden Funktionen ist für die praktische Anwendung allerdings ungeeignet. Wenn beispielsweise Bob für eine Nummer x den Code a(x) erfährt, kann er hieraus leicht den von Alice verwendeten Summanden 25 berechnen. Damit erfährt er die gesamte Funktion a und kann alle Codes von Alice entschlüsseln. Wir wollen nur erwähnen, dass man für praktische Anwendungen nicht nur die Codes 0 bis 51 verwendet, sondern auch größere Zahlen, etwa einhundertstellige Zahlen. Dann ist es nicht mehr möglich, die Codierungstabellen vollständig aufzuschreiben, weil sie zu lang sind. Auf die Details der verwendeten kommutierenden Funktionen wollen wir hier nicht näher eingehen.

Festlegung auf die verwendeten Codierungstabellen

Mit a und b bezeichnen wir die Codierungstabellen, die Alice und Bob gewählt haben. Wie oben verwenden wir eine Einwegfunktion f. Alice berechnet f (a) und sendet diesen Wert an Bob. Ebenso berechnet Bob den Wert f (b) und sendet ihn an Alice. Aus den Werten f (a) bzw. f (b) können Bob bzw. Alice auf effiziente Weise keine Informationen über die Codierungstabelle des Partners erhalten, da f eine Einwegfunktion ist. Andererseits haben sich die Spieler damit auf die Codierungstabellen a bzw. b festgelegt. Nach Ende des Spiels sendet Alice die Codierungstabelle a an Bob, der dann f (a) berechnen kann und somit überprüfen kann, ob a wirklich die Codierungstabelle ist, auf die sich Alice durch Übersenden von f (a) festgelegt hat. Ebenso kann Alice prüfen, ob die am Ende des Spiels von Bob angegebene Tabelle die ist, auf die er sich zu Beginn festgelegt hat.

Verpacken von Karten in Umschläge

Wenn Alice die Karte x in einen Umschlag verpacken möchte, berechnet sie einfach a(x). Wenn sie die Karte aus dem Umschlag a(x) entnehmen möchte, genügt es, die Umkehrfunktion a^-1 auf a(x) anzuwenden, denn a^-1(a(x))=x. Ebenso kann Bob mit Hilfe der Funktion b die Karten in Umschläge verpacken. Da wir sowohl für die Karten als auch die Codierungen (also die Umschläge) die Zahlen 0 bis 51 verwenden, kann Alice auch von Bob erzeugte Umschläge der Form b(x) in ihre Umschläge verpacken, indem sie a(b(x)) berechnet.

Das Protokoll für die Briefpost sah vor, dass zuerst Bob die Karten in Umschläge verpackt und anschließend Alice die Umschläge in eine zweite Schicht von Umschlägen verpackt. Bob sollte also zuerst b(0),...,b(51) berechnen. Man überlegt leicht, dass dies genau die Zahlen 0 bis 51 sind. Ebenso sollte Alice anschließend a(b(0)),...,a(b(51)) berechnen, was wiederum genau die Zahlen 0 bis 51 sind. Alice und Bob wissen also, dass zu Beginn die Codes 0 bis 51 vorhanden sind. Diese fassen sie als a(b(0)),...,a(b(51)) auf. Da Alice b nicht kennt, kann sie zu keinem Code bestimmen, welches die codierte Karte ist. Ebenso kann Bob dies nicht, da er a nicht kennt.

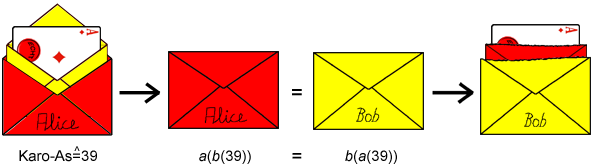
Auswahl von Karten für Alice

Bob wählt aus der Liste der noch vorhandenen Codes (zu Beginn 0 bis 51) für jede Karte, die Alice erhalten soll, einen Code zufällig aus und streicht den gewählten Code aus der Liste. Da er a nicht kennt, hat er keine Möglichkeit, Einfluss auf die gewählten Karten zu nehmen. Wenn a(b(x)) ein von Bob gewählter Code ist, wendet er auf diesen b^-1 an und erhält b^-1(a(b(x)))=b^-1(b(a(x)))=a(x), da a und b kommutieren und b^-1(b(z))=z gilt. Bob sendet dann den Wert a(x) zusammen mit a(b(x)) an Alice. Alice kann dann auf a(x) die Funktion a^-1 anwenden und erhält somit die Nummer x der Karte. Weiterhin kann sie a(b(x)) aus der Liste der noch vorhandenen Codes streichen, sodass sichergestellt ist, dass diese Karte nicht noch einmal vergeben wird.

Auswahl von Karten für Bob

Alice wählt aus den noch vorhandenen Codes für jede Karte, die Bob erhalten soll, einen Code zufällig aus. Da sie b nicht kennt, kann auch sie keinen Einfluss darauf nehmen, welche Karte gewählt wird. Wenn a(b(x)) ein solcher von Alice gewählter Code ist, wendet sie hierauf a^-1 an und erhält a^-1(a(b(x)))=b(x), da a^-1(a(z))=z gilt. Den Wert b(x) sendet sie zusammen mit a(b(x)) an Bob. Aus b(x) kann Bob wieder x, also die Nummer der gewählten Karte erhalten. Weiterhin kann er a(b(x)) aus der Liste der noch vorhandenen Codes streichen.

Weglegen von Karten

Wenn ein Spieler eine Karte x weglegen will, sendet er dem anderen Spieler eine entsprechende Mitteilung zusammen mit dem Code a(b(x)). Wie bereits festgestellt, kann der andere Spieler nicht die zugehörige Karte x herausfinden, da er entweder a oder b nicht kennt.

Besondere Eigenschaften der elektronischen Umschläge

Wir vergleichen nun die Umschläge aus Papier mit den elektronischen Umschlägen: Dazu betrachten wir noch einmal die Auswahl der Karten für Alice. Dem Verpacken der Karten in gelbe Umschläge durch Bob entspricht die Anwendung der Funktion b. Dem Verpacken dieser Umschläge in rote Umschläge durch Alice entspricht die Anwendung der Funktion a. Nach Auswahl der Karten für Alice entfernt Bob die inneren gelben Umschläge (Anwendung von b^-1) ohne die äußeren roten Umschläge zu öffnen oder etwas über den Inhalt der inneren gelben Umschläge zu erfahren. Alice kann schließlich die roten Umschläge öffnen (Anwendung von a^-1). Die elektronischen Umschläge haben also Eigenschaften, die man mit Umschlägen aus Papier nicht realisieren kann:

• Alice kann die gelben Umschläge nicht öffnen, Bob kann die roten Umschläge nicht öffnen. Das heißt insbesondere, dass nicht mehr überprüft werden muss, ob die Spieler die nicht verwendeten Umschläge auch nicht geöffnet haben, da sie dies nicht können.
  
• Man kann Umschläge zusammen mit ihrem Inhalt kopieren, ohne dazu etwas über den Inhalt wissen zu müssen oder zu erfahren.
  
• Ein roter Umschlag, der einen gelben Umschlag mit einer Karte enthält, stimmt mit einem gelben Umschlag, der einen roten Umschlag mit derselben Karte enthält, überein. Somit ist es auch möglich, zuerst den gelben Umschlag zu entfernen, auch wenn die Karte zuerst in einen gelben und dieser dann in einen roten Umschlag gesteckt wurde.
  

Kontrolle, ob fair gespielt wurde

Nach Ende des Spiels können die Spieler ihren Partnern die Codierungstabellen a bzw. b mitteilen. Dann können beide f (a) bzw. f (b) berechnen und somit überprüfen, ob dies wirklich die Codierungstabelle ist, auf die sich der andere zu Beginn festgelegt hat. Mit Hilfe der Codierungstabellen können dann beide Spieler überprüfen, ob ihre Partner Fehler bei den Berechnungen gemacht haben oder fair gespielt haben. Während des Spiels können die Spieler Umschläge nur gemeinsam öffnen, da man zum Öffnen beide Funktionen a und b kennen muss.  Daher ist es nicht mehr nötig, dass sich die Spieler später noch einmal treffen, um zu überprüfen, ob die nicht verwendeten Umschläge immer noch verschlossen sind.

Pokern mit mehr als zwei Spielern

Bis jetzt haben wir nur die Situation mit zwei Spielern betrachtet. Was passiert bei drei oder mehr Spielern? Man kann natürlich versuchen, das oben beschriebene Verfahren auf mehrere Spieler zu verallgemeinern. Es gibt aber ein grundsätzliches Problem. Unser Ausgangspunkt war, dass die Spieler sich nicht gegenseitig beobachten können. Wie also will der dritte Spieler verhindern, dass Alice und Bob zwischendurch telefonieren und Informationen über ihre Karten austauschen? Bei kommerziellen Online-Poker-Systemen besteht eine Möglichkeit darin, Spieler einander so zuzuordnen, dass sie sich höchstwahrscheinlich nicht gegenseitig kennen. Eine weitere Möglichkeit besteht darin, Auffälligkeiten im Verhalten der Gegenspieler zu finden, beispielsweise, wenn immer der Gegenspieler mit den schlechteren Karten passt. Aber selbst dann dürfte ein Betrug nur schwer nachzuweisen sein. Wenn man also in einer größeren Runde spielen will, sollte man sich trotz Computer und Internet weiterhin treffen, was ja vielleicht auch einfach mehr Spaß macht.