Autor
Rolf H. Möhring, TU Berlin
Martin Oellrich, TU Berlin
Robert Pankrath, TU Berlin
Eine Primzahl ist eine natürliche Zahl mit der Eigenschaft,
dass sie durch keine andere natürliche Zahl außer 1 und sich selbst ohne
Rest teilbar ist. Primzahlen sind in der Menge aller natürlichen Zahlen
unregelmäßig verteilt und haben dadurch Mathematiker seit tausenden von
Jahren fasziniert und beschäftigt.
Eine Primzahlentabelle bis n ist eine Liste aller Primzahlen
zwischen den Zahlen 1 und n. Sie beginnt folgendermaßen:
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | ... |
Im Laufe der Zeit sind viele Problemstellungen gefunden worden, in denen Primzahlen eine Rolle spielen. Nicht alle konnten bisher restlos geklärt werden. Hier zwei Beispiele.
Christian Goldbach (1694-1764) formulierte 1742 eine interessante Beobachtung:
| 4 = 2 + 2, | 6 = 3 + 3, | 8 = 3 + 5, | 10 = 3 + 7 = 5 + 5, | etc. |
Diese Behauptung verlangt nur, dass es mindestens eine solche Darstellung gibt. Tatsächlich gibt es für die meisten Zahlen sogar mehrere. Das folgende Diagramm wurde mit Hilfe einer Primzahltabelle erstellt und zeigt die Anzahlen solcher Darstellungsmöglichkeiten. Auf der x-Achse stehen die zerlegten (geraden) Zahlen.

Der leichte Aufwärtstrend in den Säulen setzt sich bei wachsendem n
immer weiter fort und es wurde keine gerade Zahl gefunden, für die diese
Behauptung nicht gilt. Dennoch konnte bis heute kein Beweis gefunden werden,
dass sie für alle gilt.
Carl Friedrich Gauß (1777-1855) untersuchte die Verteilung der Primzahlen,
indem er sie zählte. Er betrachtete die Funktion
Ein Diagramm dieser Funktion sieht so aus:
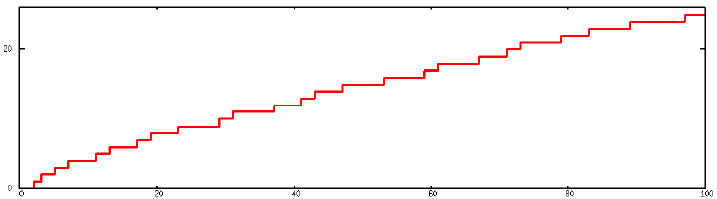
Man nennt π(n) aus offensichtlichen Gründen eine Treppenfunktion.
Gauß konstruierte dazu eine „glatte“ Kurve, die so nah wie möglich bei
π(n) bleibt, egal wie groß n wird. Um sich ein Bild von seinem Vorhaben
zu machen und sein Ergebnis später zu kontrollieren brauchte er eine
Primzahltabelle.
(Dieses Problem ist seitdem gelöst, ein tieferes Eingehen
würde jedoch den Rahmen sprengen.)
Heute sind Primzahlen nicht mehr nur eine Herausforderung für Mathematiker,
sondern von ganz praktischem Wert. So spielen etwa 100-stellige Primzahlen in
der elektronischen Verschlüsselung von Daten eine zentrale Rolle.
Von der Idee zum Verfahren
Soweit wir heute wissen, hat ein Grieche den ersten Algorithmus zur Berechnung von Primzahltabellen vorgestellt: Eratosthenes von Kyrene (ca. 276-194 v. Chr.). Er war ein hochrangiger Gelehrter im antiken Alexandria und ein Leiter der berühmten Bibliothek, in der das gesamte Wissen der damaligen Zeit gesammelt war. Er arbeitete mit an den damals wesentlichen Fragen der Astronomie, Geologie und Mathematik: Welchen Umfang hat die Erde? Woher kommt der Nil? Wie kann man aus einem Würfel einen zweiten konstruieren, der das doppelte Volumen hat?
Wir wollen im Weiteren nachvollziehen, wie er aus einer einfachen Grundidee ein
praktikables Verfahren entwickelt hat, das schon zu seiner Zeit gut auf
Papyrus oder Sand auszuführen war. Dabei wollen wir untersuchen, wie
schnell dieser Algorithmus in der Praxis ist, wenn wir eine recht große
Primzahltabelle berechnen wollen. Nehmen wir als Maßstab für
„groß“ die Zahl eine Milliarde, also
n = 109.
Eine einfache Idee
Gemäß der Definition von Primzahlen gilt für jede Zahl m, die keine Primzahl ist: es gibt zwei Zahlen i,k mit den Eigenschaften 2 ≤ i,k ≤ m und i ⋅ k = m. Diese Gesetzmäßigkeit können wir benutzen, um einen sehr einfachen Algorithmus für eine Primzahltabelle zu formulieren:
Primzahltabelle (Grundidee) schreibe alle Zahlen von 2 bis n in eine Liste bilde alle Produkte i ⋅ k, wobei i und
k
Zahlen zwischen 2 und n sind streiche alle Ergebnisse, die vorkommen, aus der Liste
Dass diese einfache Vorschrift das Gewünschte leistet, ist sofort zu
sehen: alle Zahlen, die am Schluss noch in der Liste stehen, kamen nicht als
Produktergebnis vor. Sie können also nicht als ein solches Produkt
geschrieben werden und sind demnach Primzahlen.
Wie schnell läuft die Berechnung?
Um nun zu untersuchen, was der Algorithmus an welcher Stelle genau tut, schreiben wir die in der Grundidee enthaltenen Handlungsvorschriften etwas formaler und geben den Zeilen Nummern:
Primzahltabelle_Grundversion
Steht bei Ausführung von Schritt 4 die Zahl i ⋅ k nicht in der Liste,
so passiert nichts.
Dieser Algorithmus kann ohne Schwierigkeiten auf einem Computer programmiert
werden und wir können seinen Zeitverbrauch untersuchen. Auf einem LINUX PC
(3.2 GHz) ergeben sich folgende Laufzeiten:
| n | 103 | 104 | 105 | 106 |
| Zeit | 0.00 s | 0.20 s | 19.4 s | 1943.4 s |
Es ist gut zu erkennen, dass eine Erhöhung von n um den Faktor 10 eine
Verlängerung der Rechenzeit um einen Faktor von ca. 100 mit sich bringt. Das
ist auch zu erwarten, denn sowohl i als auch k laufen über
einen ca.
10-mal so großen Bereich. Es werden also ca. 100-mal soviele Produkte
i ⋅ k gebildet.
Daraus können wir schon jetzt sehen: um auf n = 109 zu kommen, müssten
wir die Zeit bei n = 106 um den Faktor (109 /
106)2 = 106
erhöhen und würden dafür 1943 ⋅ 106 Sekunden = 61 Jahre und 7 Monate
brauchen. Das ist natürlich untauglich für die Praxis.
Womit verbringt der Algorithmus seine Zeit?
Er erzeugt alle Produkte i ⋅ k in einem gewissen Bereich:

Jedoch wird jedes einzelne Ergebnis nur einmal benötigt. Danach ist es aus der Liste entfernt und der Algorithmus bräuchte es eigentlich nie wieder zu erzeugen. Wo macht er Arbeit zuviel? Zum Beispiel dort, wo i und k genau vertauschte Werte haben, z.B. i = 3, k = 5 und später i = 5, k = 3. In beiden Fällen ist das Ergebnis des Produkts dasselbe, wie uns die Vertauschungsregel der Multiplikation lehrt: es ist immer i ⋅ k = k ⋅ i. Deshalb können wir k ≥ i festlegen, um diese Doppelungen zu vermeiden:
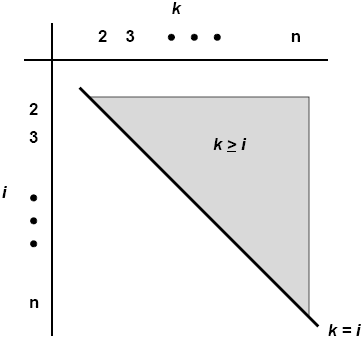
Diese Idee spart auf Anhieb die halbe Arbeit! Jedoch sind auch 30 Jahre und 10
Monate noch zu lange für unsere Tabelle. Wo können wir noch Arbeit sparen?
Dort, wo in Schritt 4 sowieso nichts passiert, wenn nämlich
i ⋅ k > n ist. Die Liste enthält ja nur Zahlen bis n, jenseits
von n ist nichts zu streichen.
Um das zu erreichen, brauchen wir die k-Schleife (Zeile 3) nur für solche
Werte auszuführen, für die i ⋅ k ≤ n ist. Diese Bedingung selbst
sagt uns, welche k das sind: k ≤ n / i.
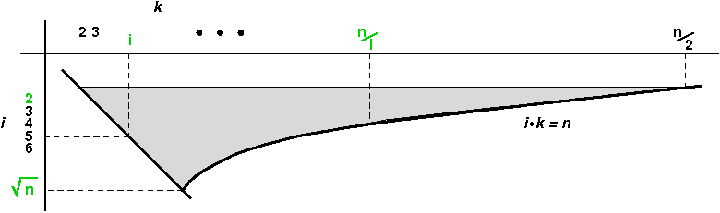
Als willkommenen Nebeneffekt können wir auch den Laufbereich für i begrenzen.
Aus den beiden Einschränkungen i ≤ k ≤ n/i erhalten wir
i² ≤ n, also i ≤ √n. Für höhere i ist der k-Bereich
leer.
Der Algorithmus hat bis hierher das folgende Aussehen bekommen:
Primzahltabelle_besser_1
(Das Zeichen ⌊&sdot⌋ bedeutet Abrundung, denn i und k
können nur ganzzahlige Werte annehmen.)
Wie schnell sind wir jetzt geworden? Die neuen Laufzeiten:
| n | 104 | 105 | 106 | 107 | 108 | 109 |
| Zeit | 0.00 s | 0.01 s | 0.01 s | 2.3 s | 32.7 s | 452.9 s |
Der Effekt ist recht spürbar, denn das Ziel 109 ist schon in
Reichweite: nur noch siebeneinhalb Minuten entfernt. Lassen wir den Computer
in Gedanken laufen und nutzen diese Zeit, um es vielleicht noch besser zu
machen!
Brauchen wir jeden i-Wert?
Schauen wir an, was innerhalb der i-Schleife (Zeile 2) genau passiert:
i bleibt fest und k durchläuft seine Schleife (Zeile 3). Dabei erhält
das Produkt i ⋅ k die Werte
| i², | i(i+1), | i(i+2), | ... |
Wenn die k-Schleife zu Ende gelaufen ist, stehen in der Liste keine echten Vielfachen mehr von i. Ebenso nicht von allen Zahlen kleiner als i, denn sie wurden auf dieselbe Weise schon vorher gestrichen.
Was passiert, wenn i keine Primzahl ist? Beispiel i = 4 : das Produkt i ⋅ k durchläuft die Werte 16, 20, 24, ... . Jedoch sind diese Zahlen alle auch Vielfache von 2, da 4 selbst Vielfaches von 2 ist. Es ist im Grunde für i = 4 gar nichts zu tun. Ebenso ist das mit jeder anderen geraden Zahl i > 4.
Beispiel i = 9 : das Produkt i ⋅ k durchläuft nur Vielfache von 9. Die sind aber als Vielfache von 3 schon durchlaufen und ebenfalls unnötig. So ist das mit allen Nichtprimzahlen, denn sie haben einen kleineren Primteiler, der vor ihnen schon ein Wert für i war. Wir brauchen also die k-Schleife nur für Primzahlen i auszuführen:
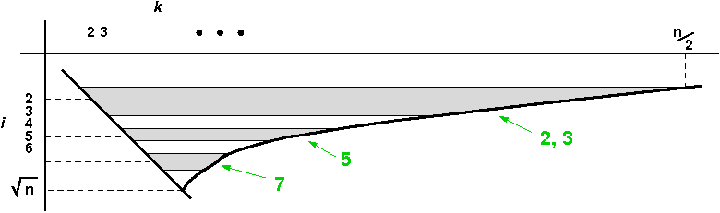
Ob nun i eine Primzahl ist oder nicht, könnte uns die Liste selbst sagen
- wenn sie schon fertig wäre. Wir können aber erst nach dem Ende des
Algorithmus sicher sein, dass nur noch Primzahlen in der Liste stehen. Oder?
Ja und nein. Im allgemeinen Ja, denn sonst könnten wir den
Algorithmus abkürzen. Das ist nicht immer der Fall, nehmen wir zum Beispiel
n = 100 : die Nichtprimzahl 91 muss irgendwann aus der Liste gestrichen
werden. Sie wird aber erst ganz kurz vor dem Ende erzeugt, nämlich für
i = 7, k = 13.
In unserem speziellen Fall aber Nein, denn wir wollen ja nicht jede
beliebige Zahl als Primzahl erkennen, sondern eine ganz bestimmte, die
Zahl i. Und das auch nicht zu beliebiger Zeit, sondern erst zum Anfang der
k-Schleife für den Wert i. Hier gibt uns die Liste eine korrekte
Auskunft! Warum?
Wir hatten oben beobachtet, dass für jedes feste i alle gestrichenen Werte
i ⋅ k ≥ i² sind. Anders ausgedrückt: im
Zahlenbereich 2, ..., i² - 1 wird nichts verändert.
Da i im weiteren Verlauf nur steigt, wächst auch dieser Bereich und enthält
alle Bereiche vor ihm. Im folgenden Bild sind diese Bereiche blau dargestellt:

Da innnerhalb dieser Bereiche bis zum Ende des Algorithmus keine Veränderungen
mehr auftreten, müssen sie bereits vor dem Durchlauf der
k-Schleife für das jeweilige i korrekt sein. Die Tabelle wird sozusagen
in quadratischen Sprüngen fertig. Grün eingezeichnet ist der Wert i selbst,
den wir auf seine Primeigenschaft prüfen wollen. Es ist gut zu erkennen, dass
er immer in einem blauen Bereich liegt. Um zu entscheiden, ob i eine Primzahl
ist, dürfen wir also einfach in der aktuellen Liste nachschauen.
Wir können im Algorithmus die i-Schleife jetzt wie folgt ergänzen:
Primzahltabelle_Eratosthenes
Diese Version des Verfahrens hatte der kluge Grieche vorgestellt und es
heißt nach seinem Erfinder das Sieb des Eratosthenes.
Sieb deswegen, weil es die gewünschten Objekte, die Primzahlen,
nicht gezielt konstruiert, sondern im Gegenteil alle Nichtprimzahlen
aussondert.
Unsere Zeitmessung sagt zu seinem Algorithmus:
| n | 106 | 107 | 108 | 109 |
| Zeit | 0.02 s | 0.43 s | 5.4 s | 66.5 s |
Bei n=109 nur noch gut eine Minute!
Geht es noch schneller?
Mit einem ähnlichen Argument wie für die i-Werte können wir auch die Werte der k-Schleife
weiter einschränken: wir brauchen nur diejenigen zu betrachten, die in der
Liste gefunden werden. Steht k nämlich nicht mehr dort, ist k als
Nichtprimzahl gestrichen worden und besitzt einen Primteiler p < k.
Im Durchgang der i-Schleife mit i = p wurden alle Vielfachen von
p gestrichen, insbesondere k und seine Vielfachen. Es ist an
dieser Stelle nichts mehr zu tun.
Es wäre nun nahe liegend, den Algorithmus wie folgt zu ergänzen:
3 für jede Zahl
k := i...⌊n/i⌋ in der Liste
führe aus: 4 ...
Doch Achtung! Diese Formulierung hat ihre Tücken. Lassen wir den Algorithmus so laufen, erzeugt er die folgende Tabelle:
| 2 | 3 | 5 | 7 | 8 | 11 | 12 | 13 | 17 | 19 | 20 | 23 | 27 | 28 | 29 | 31 | 32 | 37 | 41 | 43 | 44 | ... |
Was läuft falsch? Sehen wir uns die ersten Schritte des Algorithmus genau an. Nach der Initialisierung der Liste mit allen Zahlen bis n (Zeile 1) steht darin:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ... |
Zunächst wird i = 2 gesetzt und dann k = 2 . Die 2 steht in der Liste, also wird i ⋅ k = 4 gestrichen:
| 2 | 3 | - | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ... |
Im nächsten Schritt ist k = 3 . Die 3 steht ebenfalls in der Liste und so wird i ⋅ k = 6 gestrichen:
| 2 | 3 | - | 5 | - | 7 | 8 | 9 | 10 | 11 | ... |
Jetzt passiert′s: k = 4 steht nicht mehr in der Liste, denn sie wurde ja als erste gestrichen. Entsprechend wird für k = 4 wegen der neuen Bedingung nichts gemacht und der Algorithmus fährt mit k = 5 fort:
| 2 | 3 | - | 5 | - | 7 | 8 | 9 | - | 11 | ... |
So bleibt 2 ⋅ 4 = 8 irrtümlich in der Liste stehen. Das Problem ist, dass k beim Schleifendurchlauf stets größere Zahlen i ⋅ k > k streicht und dann selbst erhöht wird. Irgendwann bekommt k den Wert eines vormaligen Produktes i ⋅ k und das Verfahren wirkt ungünstig auf sich selbst zurück:
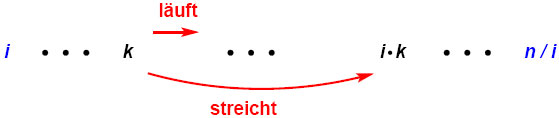
Die Lösung besteht darin, k seinen Schleifenbereich rückwärts durchlaufen zu lassen. Dadurch wird diese Rückwirkung vermieden:

Mit dieser Überlegung werden nur noch die folgenden Produkte i ⋅ k gebildet:

Insgesamt ergibt sich nun die folgende Version des Algorithmus:
Primzahltabelle_besser_3
Seine Laufzeiten:
| n | 106 | 107 | 108 | 109 |
| Zeit | 0.01 s | 0.15 s | 1.6 s | 17.6 s |
Dieses Ergebnis ist für heutige Standards durchaus akzeptabel. Wir haben ausgehend von der naiven Grundversion mit wenigen gezielten Überlegungen den Algorithmus für n = 109 um den Faktor 254.5 Millionen beschleunigt!
Im nachfolgenden Applet könnt ihr euch für verschiedene Werte von n anschauen, welche Werte für i, k und i ⋅ k der Algorithmus in seinen Varianten durchläuft. (Erwartet die guten Rechenzeiten nicht von dem Applet. Mehr als n = 104 schafft es nicht.)
Was können wir aus diesem Beispiel lernen?
- Einfache Rechenverfahren sind nicht automatisch effizient,
- zu ihrer Beschleunigung muss man sie gut verstehen,
- es sind oft viele Verbesserungen möglich,
- mathematische Ideen können sehr weitreichend sein!
- Wissenswertes über Eratosthenes:
- direkte Tests für große Primzahlen

