Autoren
Katharina Langkau, TU Berlin
Martin Skutella, Universität Dortmund
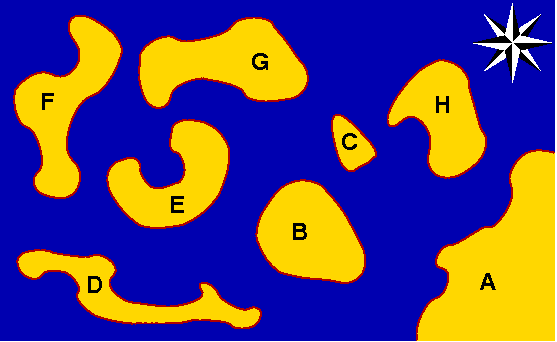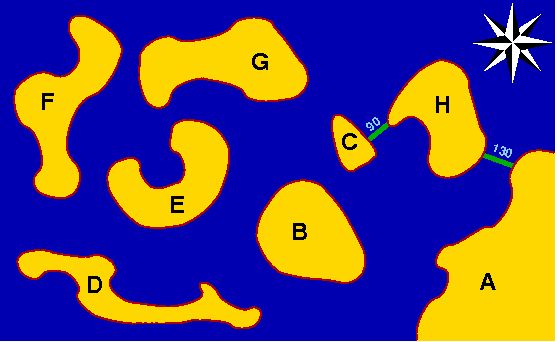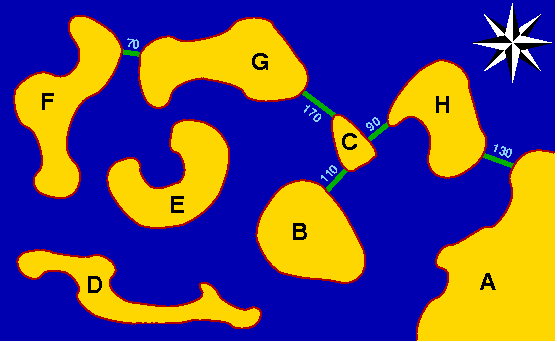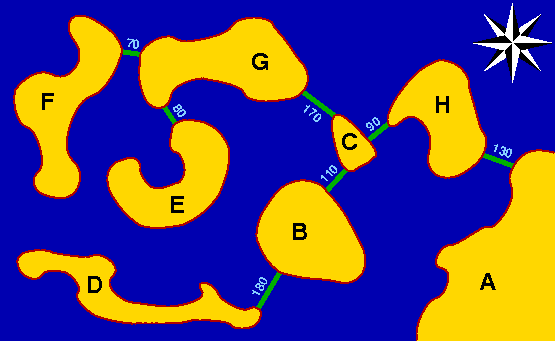
Einst lebte in einem fernen Inselreich der Stamm der Algolaner. Die Stammesmitglieder hausten verstreut auf allen sieben Inseln des unten abgebildeten Inselreichs.
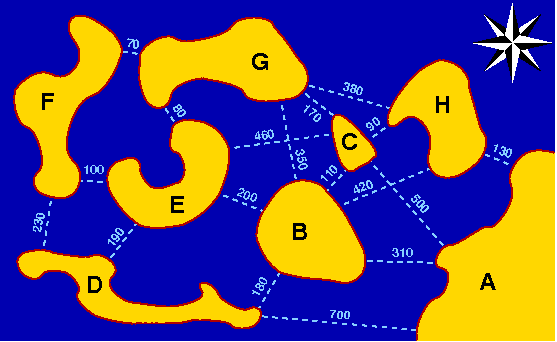
Zwischen den sieben Inseln und dem Festland verkehrten mehrere Fähren, die gegenseitige Besuche und Ausflüge auf das Festland ermöglichten. Die Fährverbindungen sind in der Karte gestrichelt eingezeichnet. Die Zahlen geben die Länge der Fährverbindungen in Metern an.
Bei stürmischem Wetter kam es regelmäßig vor, dass eine Fähre kenterte. Deshalb beschlossen die Algolaner, einige Fährverbindungen durch Brücken zu ersetzen.
Im ersten Jahr sollte durch den Bau einer Brücke eine der sieben Inseln an das Festland angeschlossen werden. Die Algolaner wählten die Brücke der Länge 130m zwischen A und H, da die Verbindungen von A zu anderen Inseln länger sind.
Im zweiten Jahr wollte man eine weitere Insel an das Festland anschließen. In Frage kam also der Bau einer Brücke von A oder von H aus zu einer der anderen Inseln. Die Algolaner entschieden sich für die kürzest mögliche Brücke der Länge 90m zwischen C und H.
Im dritten Jahr wollte man mit dem Bau einer weiteren Brücke (von A, C oder H aus) eine dritte Insel mit dem Festland verbinden. Die kürzest mögliche Variante war dieses Mal die Brücke der Länge 110m zwischen B und C.
In den folgenden Jahren wurden die Brücke der Länge 170m zwischen C und G, dann die Brücke der Länge 70m zwischen F und G, als nächstes die Brücke der Länge 80m zwischen E und G und schließlich die Brücke der Länge 180m zwischen B und D gebaut.
Nach Ablauf des siebten Jahres waren also alle Inseln untereinander und mit dem Festland durch Brücken verbunden. Das Brückenprojekt war damit abgeschlossen. In der folgenden Animation kannst du den zeitlichen Verlauf des Brückenbauprojekts nachverfolgen.
Die Algolaner waren sehr zufrieden, da der Aufwand für den Bau der Brücken zwar groß gewesen war, man aber andererseits überzeugt war, keine unnötig langen Brücken gebaut zu haben. Die Länge aller Brücken zusammen betrug, wie du leicht nachrechnen kannst, genau 830m.
Kurz nach Fertigstellung der letzten Brücke fegte ein wütender Orkan über das Inselreich und zerstörte die mühsam errichteten Brücken. Nachdem sie sich von dem Schock erholt hatten, beschlossen die Algolaner, ein neues Brückensystem zu errichten. Die neuen Brücken sollten wieder alle Inseln untereinander und mit dem Festland verbinden.
In Folge des Orkans war das Baumaterial knapp geworden. Man einigte sich darauf, zunächst eine möglichst kurze Brücke zu bauen. Daher wurde im ersten Jahr die Brücke der Länge 70m zwischen F und G errichtet.
Auch im zweiten Jahr war nur wenig Material vorhanden, so dass man die nächst längere Brücke der Länge 80m zwischen E und G errichtete.
Im dritten Jahr wurde gemäß dieser Strategie die Brücke der Länge 90m zwischen C und H gebaut.
Nach dem Bau dieser drei Brücken waren die drei Inseln E, F und G und die beiden Inseln C und H miteinander verbunden. Die kürzeste noch nicht bestehende Verbindung war im vierten Jahr die der Länge 100m zwischen E und F. Da diese beiden Inseln jedoch bereits über G miteinander verbunden waren, errichtete man statt dessen die Brücke der Länge 110m zwischen B und C.
Im fünften Jahr kam die Brücke der Länge 130m zwischen A und H hinzu. Danach die Brücke der Länge 170m zwischen C und G und schließlich im siebten Jahr die Brücke der Länge 180m zwischen B und D.
Den zeitlichen Verlauf des zweiten Brückenbauprojekts kannst du in der Animation nachverfolgen.

Trotz der veränderten Strategie bei der Auswahl der Brücken war wieder das gleiche Brückensystem der Länge 830m entstanden. Dies bestärkte die Algolaner in ihrer Auffassung, das optimale Brückensystem für ihre Inseln gefunden zu haben. Und wenn kein zweiter Orkan sein Unwesen über dem Inselreich getrieben hat, dann spazieren die Algolaner noch heute glücklich und stolz über ihre Brücken...
Jetzt fragst du dich bestimmt, ob die Algolaner zurecht so stolz auf ihr Brückensystem waren. Vielleicht gibt es ja doch ein besseres, also kürzeres Brückensystem? Du kannst dich durch Ausprobieren davon überzeugen, dass jedes andere Brückensystem, das alle sieben Inseln und das Festland miteinander verbindet, länger als 830m ist.
Ein Brückensystem minimaler Gesamtlänge, das einige Orte (hier das Festland A und die Inseln B bis H) miteinander verbindet, heißt "minimaler aufspannender Baum". Das Problem, einen minimalen aufspannenden Baum zu finden, hat neben dem Brückenbau zahlreiche andere praktische Anwendungen. Es tritt beispielsweise auf, wenn Grundstücke eines Neubaugebietes möglichst kostengünstig an die Kanalisation angeschlossen werden sollen. Andere Anwendungen tauchen beim Entwurf von Computer-Chips und bei der Planung von Verkehrs- oder Kommunikationsnetzen (Telefon, Fernsehen, Internet etc.) auf.
Hinter den beiden Strategien der Algolaner stecken bekannte Algorithmen zur Lösung des Problems. Die erste Strategie ist unter dem Namen "Algorithmus von Prim" bekannt. Dieser Algorithmus bindet die Orte nacheinander an das Festland an. Dabei wird in jedem Schritt die kürzest mögliche Brücke gebaut.
Algorithmus von Prim
Wähle einen speziellen Ort aus (Festland) und nenne ihn erreichbar. Alle anderen Orte sind zunächst nicht erreichbar. Führe den folgenden Schritt so oft aus, bis alle Orte erreichbar sind: Baue die kürzeste Brücke zwischen zwei Orten, von denen einer erreichbar und der andere nicht erreichbar ist, und nenne den bislang nicht erreichbaren Ort erreichbar.
Die zweite oben beschriebene Strategie (nach dem Orkan) ist unter dem Namen "Algorithmus von Kruskal" bekannt. Dieser Algorithmus baut in jedem Schritt die kürzeste Brücke, die zwei noch nicht miteinander verbundene Orte verbindet. Er unterscheidet sich von dem Algorithmus von Prim darin, dass er nicht nur Brücken in Betracht zieht, die eine Verbindung zum Festland herstellen, sondern den Bau beliebiger Brücken zwischen bislang unverbundenen Orten erlaubt.
Algorithmus von Kruskal
Führe den folgenden Schritt so oft aus, bis alle Orte untereinander durch Brücken verbunden sind: Baue die kürzeste Brücke, die zwei Orte verbindet, die bislang nicht voneinander aus erreichbar sind.
Die Algorithmen von Prim und Kruskal berechnen einen minimalen aufspannenden Baum. Sie haben eine weitere Gemeinsamkeit. Führ dir noch einmal das Vorgehen der Algolaner vor Augen. Bei beiden Verfahren haben die Algolaner relativ kurzsichtig von Jahr zu Jahr geplant. Sie haben jedes Jahr die beste (d.h. kürzeste) Brücke gebaut, die zu dem Zeitpunkt in Frage kam. Dabei haben sie keine Rücksicht darauf genommen, welche Auswirkungen die getroffene Entscheidung für den weiteren Verlauf des Brückenbauprojekts hat. Wie du siehst, kann auch das "Naheliegende" einmal zum Erfolg führen.
Algorithmen mit dieser Eigenschaft werden auch "greedy" (englisch für "gierig") genannt, weil sie in jedem Schritt die beste Wahl treffen, die momentan zur Verfügung steht. Solch ein "kurzsichtiger" Ansatz führt bei anderen Problemen nicht immer zum Ziel. Stelle dir beispielsweise vor, Du sollst nur die Insel D durch ein Brückensystem minimaler Länge an das Festland A anbinden. In dem kurzsichtig entworfenen Brückensystem der Algolaner erreicht man D von A aus über die Inseln H, C und B. Für diesen Weg ergibt sich eine Gesamtlänge von 510m. Bestimmt kannst du eine kürzere Verbindung zwischen A und D finden! (Wenn du mehr darüber erfahren möchtest, wie man algorithmisch die kürzeste Verbindung vom Festland A zu der Insel D findet, dann schau doch mal beim 7. Algorithmus der Woche nach.)
Die beiden Algorithmen haben übrigens eine weitere interessante Eigenschaft. Sie berechnen immer eine Lösung, in der die Länge der längsten Brücke so klein wie möglich ist. Am Beispiel des Inselreichs kannst du das überprüfen.
- Robert C. Prim (Wikipedia)
- Joseph Kruskal (Wikipedia)

