Peter Sanders, Universität Karlsruhe
Johannes Singler, Universität Karlsruhe
Stephan Kupferer, Universität Karlsruhe
Ich bin gerade nach Karlsruhe in meine erste Studentenbude gezogen. So eine Großstadt ist schon ziemlich kompliziert. Einen Stadtplan habe ich zwar schon, aber wie finde ich heraus, wie ich am schnellsten wohin komme? Ich fahre zwar gerne Fahrrad, aber ich bin notorisch ungeduldig, deshalb brauche ich den wirklich kürzesten Weg – zur Uni, zu meiner Freundin…
Ich gehe die Planung also systematisch an. So könnte es gehen: Ich breite den Stadtplan auf einem Tisch aus und lege dünne Fäden entlang der Straßen. Diese werden an Kreuzungen und Abzweigungen miteinander verknotet. Der Einfachheit halber mache ich außerdem Knoten an allen möglichen Start- und Zielpunkten sowie an den Enden von Sackgassen.
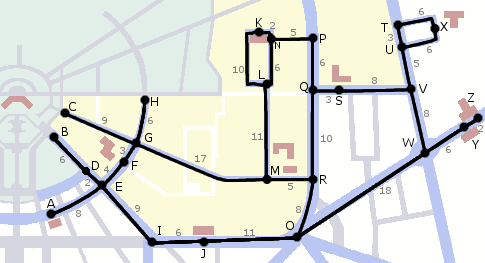
Jetzt kommt der Trick: Ich fasse das entstandene Gespinst dort, wo ich starte, und ziehe diesen Knoten langsam nach oben. Nach und nach lösen sich die anderen Knoten von der Tischplatte. Ich habe die Knoten beschriftet, so dass ich immer noch weiß, welcher Knoten wohin gehört. Schließlich hängt alles senkrecht unter dem Startknoten.
Jetzt habe ich leichtes Spiel: Um einen kürzesten Weg von meinem Startpunkt zu einem Zielpunkt zu finden, muss ich nur den Zielpunkt ausfindig machen und straff gespannte Fäden nach oben bis zum Startpunkt zurückverfolgen. Der Abstand zwischen Start- und Zielpunkt lässt sich außerdem einfach mit einen Maßband abmessen. Der so gefundene Weg muss der kürzeste sein, denn gäbe es einen noch kürzeren, hätten sich Start und Ziel nie so weit voneinander entfernt (ohne Fäden zu zerreißen).
 Nehmen wir zum Beispiel an, ich möchte den kürzesten Weg
von der Mensa (M) zum Rechenzentrum (F) herausfinden. Ich hebe das Netz
also am Knoten M immer weiter an, wobei sich Knoten für Knoten vom
Tisch löst.
Sobald Knoten F in der Luft hängt, kann ich aufhören. In nebenstehender
Zeichnung ist
das Gewirr aufgezeichnet, zur Verbesserung der übersichtlichkeit aber
ein bisschen auseinander gezogen,
nicht ganz senkrecht.
Man erkennt, dass der kürzeste Weg von M nach F über G führt. Zwischen
L und K hat sich bereits eine durchhängende Schlaufe gebildet, die sich
auch nicht mehr spannen wird. Das bedeutet, dass kein kürzester Weg von
M aus
über diese Verbindungen läuft.
Nehmen wir zum Beispiel an, ich möchte den kürzesten Weg
von der Mensa (M) zum Rechenzentrum (F) herausfinden. Ich hebe das Netz
also am Knoten M immer weiter an, wobei sich Knoten für Knoten vom
Tisch löst.
Sobald Knoten F in der Luft hängt, kann ich aufhören. In nebenstehender
Zeichnung ist
das Gewirr aufgezeichnet, zur Verbesserung der übersichtlichkeit aber
ein bisschen auseinander gezogen,
nicht ganz senkrecht.
Man erkennt, dass der kürzeste Weg von M nach F über G führt. Zwischen
L und K hat sich bereits eine durchhängende Schlaufe gebildet, die sich
auch nicht mehr spannen wird. Das bedeutet, dass kein kürzester Weg von
M aus
über diese Verbindungen läuft.
Ich habe das ganze für die Umgebung meiner Uni erfolgreich getestet. Aber schon mein erster Versuch mit ganz Karlsruhe ist kläglich an verhedderten Bindfäden gescheitert. Ich habe die halbe Nacht gebraucht, um die Fäden zu entwirren und erneut auf dem Stadtplan auszulegen.
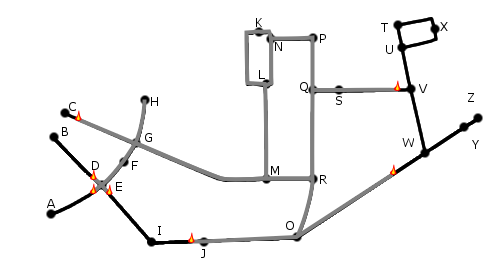
Nachdem ich diesen Pyromanen hochkant aus meiner Bude geworfen habe, beginne ich nachzudenken. Ich muss meine Scheu vor Abstraktion überwinden und das Ganze meinem dämlichen Computer verklickern. Das hat aber auch Vorteile. Fäden, die es nicht gibt, können sich nicht verheddern oder abbrennen. Mein Prof hat mir gesagt, dass ein Herr Dijkstra einen Algorithmus, der das Kürzeste-Wege-Problem ganz ähnlich wie das Bindfadenverfahren löst, schon 1959 aufgeschrieben hat. Netterweise kann man den Algorithmus von Dijkstra in der Bindfadenterminologie beschreiben.
Zu jedem Knoten muss mein Computer lediglich die von ihm ausgehenden Fäden zu benachbarten Knoten und deren Länge kennen. Er verwaltet außerdem eine Tabelle d, die zu jedem Knoten seinen Abstand zum Zielknoten abschätzt (d. h. die Entfernung ist höchstens so groß wie der entsprechende Eintrag in d). Bei hängenden Knoten ist das auch die endgültige Länge des kürzesten Weges. Bei Nachbarn hängender Knoten gibt d die Länge der kürzesten Verbindung an, welche nur über hängende Knoten geht. Nennen wir diese Knoten liegend. Bei den anderen, bisher unerreichten Knoten, ist d gleich unendlich. Anfangs ist also d[StartKnoten] = 0.
Der hier angegebene Pseudocode berechnet nun die Entfernungen aller Knoten vom Startknoten:
Was hat dieser Algorithmus mit dem Prozess des langsamen Hochhebens des Startknotens zu tun? Jede Iteration der while-Schleife entspricht dem Übergang eines Knotens v von liegend nach hängend. Da d[v] den Abstand vom Startknoten zu v mittels hängender Fäden angibt, ist der jeweils nächste angehobene Knoten derjenige mit dem kleinsten d[v] Wert. Dieser Wert entspricht der Höhe des Startknotens, bei dem v hängend wird. Da andere, später angehobene Fäden diese Höhe nicht mehr verkleinern können, entspricht d[v] auch der entgültigen Entfernung vom Start zu v. (Dieses Argument funktioniert allerdings nur für den Knoten mit dem jeweils kleinsten d[v] Wert.)
Ein richtig genialer Zug von Dijkstras Algorithmus ist, dass die d[u]-Werte der anderen Knoten sich sehr einfach anpassen lassen, wenn v hängend wird. Lediglich die von v ausgehenden Fäden müssen betrachtet werden. Dies erledigt die innere for-Schleife. Eine Faden zwischen v und einem Nachbarknoten u mit Länge L ergibt eine Verbindung vom Startknoten zu u der Länge d[v] + L. Wenn dieser Wert kleiner ist, als der bisherige Wert von d[u], wird d[u] entsprechend verringert. Am Ende hängen alle überhaupt vom Startknoten aus erreichbaren Knoten und die d[v]-Werte geben die kürzesten Weglängen an.
Das folgende Applet führt den Algorithmus von Dijkstra interaktiv aus. Ein Klick auf "Schritt" führt einen Schritt durch, "Komplett" führt den Algorithmus bis zum Ende aus. Weiße und blaue Knoten liegen noch auf dem Tisch, wobei die blauen mit bereits hängenden verbunden sind. Die orangenen Knoten hängen in der Luft. In den Knoten steht das aktuelle d[]. Nach Beendigung des Algorithmus muss man vom Zielknoten aus den roten Fäden entlang rückwärts gehen, um den kürzesten Weg zu finden. Das ist eindeutig und führt auf jeden Fall zum Startknoten. Versuchen Sie doch einmal, den Bindfadenzustand der zweiten Abbildung damit zu rekonstruieren. Für das Karlsruhe-Beispiel entspricht eine Abstands-Einheit übrigens ca. 10m in der Realität. Als weitere Beispiele können Sie noch ein abstraktes Netz sowie einen klitzekleinen Ausschnitt aus einem Routenplaner für Deutschland auswählen.
Folgende Abbildung zeigt den Zustand des Algorithmus nach 10 Schritten, also entsprechend der Bindfadenabbildung.
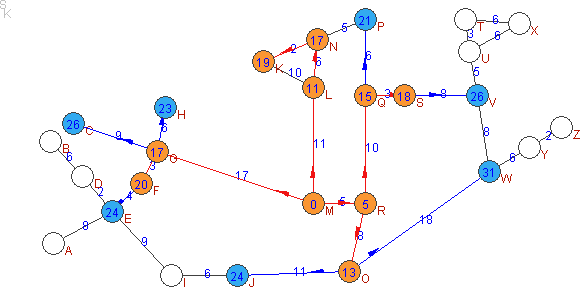
Dieser Algorithmus lässt sich leicht so erweitern, dass auch die kürzesten Wege rekonstruiert werden können: Immer wenn d[u] neu gesetzt wird, merken wir uns den Knoten v, der dafür verantwortlich war, als Vorgänger p[v]. Später rollen wir durch Zurückverfolgen der Vorgängerverweise die Route vom Ziel zum Start auf.
Natürlich gibt es auch zu diesem Beitrag viele „lose Enden“, die wir auf so engem Raum nicht verfolgen können. Einen Link auf weitere Informationen finden Sie darum weiter unten.

