Alexander Souza, Universität Freiburg
Angelika Steger, ETH Zürich
Schon faszinierend, was man so alles mit Algorithmen machen kann: CDs schnell in Regalen finden und sortieren, Zahlen richtig aussprechen und aus Labyrinthen entkommen. Ich habe gehört, dass das Buch "Introduction to Algorithms" von Cormen, Leiserson, Rivest und Stein eine umfangreiche Einführung sein soll. Ich werde es einfach mit der ISBN übers Internet bestellen.

Einfach die 10 Ziffern 0-362-03293-7 eingeben und los geht's. Hmm, komisch, der Shop sagt, dass nichts gefunden werden konnte. Ach ja, ich habe mich bei der zweiten Ziffer vertippt. Das ist die richtige Nummer: 0-262-03293-7. Bestellung abgeschickt, prima.
Hätte der Shop nicht feststellen können, dass ich mich bei der ISBN vertan habe? Was ist eigentlich ISBN?
International Standard Book Number
ISBN steht für International Standard Book Number. Diese Nummern werden verwendet um Bücher und andere Medien international einheitlich und eindeutig zu kennzeichnen. Eine ISBN besteht aus vier Zahlenblöcken, die durch Bindestriche getrennt sind:
- Sprachcode, z.B. 0 für Verlage aus dem englischsprachigen Raum und 3 für Verlage aus Deutschland, Österreich und der Schweiz,
- Verlagsnummer,
- laufende Nummer, die von den Verlagen vergeben wird und
- Prüfziffer.
Wie wir noch sehen werden, dient die Prüfziffer dazu, dass kleinere Tippfehler und Zahlendreher zu einer ungültigen ISBN führen und somit erkannt werden können. Bevor wir uns mit der Berechnung der Prüfziffer näher beschäftigen, benötigen wir noch das Konzept der modularen Arithmetik aus der Mathematik.
Modulare Arithmetik
Betrachten wir zwei beliebige natürliche Zahlen a und m und dividieren a "mit Rest" durch m: das ergibt einen (ganzzahligen) Quotienten b und einen Rest r, der eine natürliche Zahl zwischen 0 und m - 1 ist. Kurz: a = b · m + r. Wir sagen, dass die Zahl a kongruent r modulo m ist und schreiben kurz a ≡ r (mod m). Beispielsweise ist 9 kongruent 1 modulo 8, weil 9 bei Division durch 8 den Rest 1 ergibt. Die Zahl 16 ist kongruent 0 modulo 8, weil 16 ohne Rest durch 8 teilbar ist.Wir können uns dies wie das zyklische Wandern auf einem Rad vorstellen, auf dem die Zahlen 0, 1, 2, ..., m - 1 aufgetragen sind. Um a modulo m, also den Rest von a bei der Division durch m, zu bestimmen, starten wir bei 0 und gehen dann a mal (zyklisch) in Einerschritten nach rechts. Die Anzahl der Umrundungen des Rades ist der oben erwähnte Quotient, die Zahl, bei der wir landen, ist der Rest.
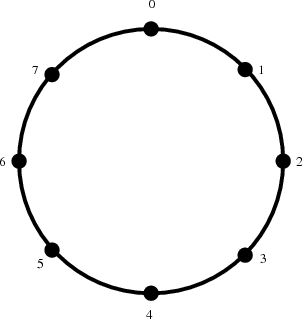
Unter modularer Arithmetik versteht man das Rechnen, also insbesondere Addition und Multiplikation, wobei das Ergebnis stets modulo einer Zahl m genommen wird. Wenn wir also a + b modulo m bestimmen wollen, berechnen wir zunächst die Zahl (a + b) und von dieser den Rest modulo m. Entsprechend geht man bei der Multiplikation vor: erst multiplizieren, dann den Rest bei der Division durch m bilden.
Prüfziffern bei ISBN
Zurück zur Berechnung der Prüfziffer. Diese ergibt sich bei der ISBN indem man eine gewichtete Quersumme der ersten neun Ziffern bestimmt: die erste Ziffer wird mit 1 multipliziert, die zweite mit 2 und allgemein die i-te Ziffer mit i. Diese Summe wird modulo 11 genommen. (Wenn der Rest dieser Summe 10 ist, so schreibt man als Prüfziffer ein X.)
Bei meiner Bestellung ist die Prüfziffer sieben: 0 · 1 + 2 · 2 + 6 · 3 + 2 · 4 + 0 · 5 + 3 · 6 + 2 · 7 + 9 · 8 + 3 · 9 = 161 = 14 · 11 + 7 ≡ 7 (mod 11).
Die Prüfziffer meiner falschen Eingabe 0-362-03293-? ist demnach 9. Wenn der Computer also die Folge 0-362-03293-7 sieht, kann er erkennen, dass etwas nicht stimmt. Der Shop hätte mich also schon warnen können, dass ich mich bei der Bestellung vertippt habe!
Erkennung von Tippfehlern
Jetzt überlegen wir uns, dass es immer erkannt werden kann, wenn wir uns bei der Eingabe einer ISBN an genau einer Stelle vertippt haben.
Zur besseren Unterscheidbarkeit schreiben wir für die (richtige) ISBN x = a1 a2 a3 a4 a5 a6 a7 a8 a9 b mit Prüfziffer b. Wie oben erklärt, ist die Prüfziffer eine ganze Zahl zwischen 0 und 10. Die Ziffernfolge, die wir eingegeben haben (also die "falsche ISBN"), bezeichnen wir mit y = c1 c2 c3 c4 c5 c6 c7 c8 c9 d. Wir nehmen an, dass wir uns an genau einer Stelle vertippt haben, d.h. y unterscheidet sich von x an genau einer Stelle.
Nehmen wir zunächst an, dass wir uns bei der Prüfziffer selbst vertan haben. In unserer Schreibweise heißt das, aj = cj für alle j von 1 bis 9 und b ≠ d. Dies kann natürlich aus den ersten neun (richtigen) Ziffern berechnet werden: c1 + 2 · c2 + … + 9 · c9 (mod 11) = b ≠ d.
Nun nehmen wir an, dass wir uns bei genau der i-ten der neun ersten Ziffern vertippt haben. Es gilt, dass ci = ai + t, wobei t eine ganze Zahl ungleich der Null ist (sonst wäre die i-te Stelle ja richtig). Alle anderen Positionen sind gleich, d.h. cj = aj für j ≠ i. Insbesondere ist b = d. Es ist zu zeigen, dass sich die Prüfziffer d der "falschen ISBN" y von der Prüfziffer b der richtigen ISBN x unterscheidet.
Wir berechnen die korrekte Prüfziffer der Zahenfolge c1 … c9:
c1 + 2 · c2 + … + 9 · c9 (mod 11) =a1 + 2 · a2 + … + i · (ai + t) + … + 9 · a9 (mod 11) =
b + i · t (mod 11)
Die Zahl b + i · t (mod 11) kann nur dann gleich d, also auch gleich b sein, wenn i · t entweder 0 oder durch 11 teilbar ist.
Da weder t noch i gleich 0 sind, kann t · i ebenfalls nicht 0 sein. Wir müssen jetzt also nur noch zeigen, dass t · i nicht durch 11 teilbar ist. Anders ausgedrückt, wir müssen nachweisen, dass t · i kein Vielfaches von 11 sein kann. Das ist leicht: 11 ist eine Primzahl, d.h., alle Vielfachen davon müssen 11 als Primfaktor enthalten. Da sowohl t als auch i kleiner als 11 sind, ist das unmöglich. Wir haben also gezeigt, dass t · i (mod 11) stets ungleich 0 ist und sich die Prüfziffern von x und y unterscheiden.
Anders sieht es aus, wenn wir uns an zwei oder mehr Stellen vertippt haben. Dann kann es passieren, dass die falsche ISBN die gleiche Prüfziffer wie die richtige hat. Beispielsweise hat die ISBN 0-262-14293-7 ebenfalls die Prüfziffer 7 und unterscheidet sich von 0-262-03293-7 an genau der fünften und sechsten Ziffer.
Wenn wir uns an mehreren Stellen vertan haben kann es sein, dass wir ein unerwünschtes Buch bekommen, das zufälligerweise die ISBN hat, die wir eingegeben haben. Hätten wir versehentlich 0-262-03295-3 eingegeben, wäre das Buch "Melancholia and Moralism" geliefert worden.
Erkennung von Zahlendrehern
Ein weiterer "beliebter" Fehler bei der Eingabe sind Zahlendreher, d.h. die Vertauschung von benachbarten Ziffern. Beispielsweise ist in der ISBN 0-226-03293-7 ein Zahlendreher an der dritten und vierten Ziffer. Mit der Prüfziffer kann erkannt werden, ob genau ein Zahlendreher der ersten neun Ziffern vorliegt. Tatsächlich, die korrekte Prüfziffer von 0-226-03293-? ist 0.
Wie oben sehen wir uns zwei Folgen x und y an, bei denen zwei benachbarte Ziffern ai und ai + 1 vertauscht sind, die aber ansonsten identisch sind. Damit wir überhaupt von einem Zahlendreher sprechen können nehmen wir an, dass ai und ai + 1 unterschiedlich sind. Wir betrachten den Fall ai > ai + 1; der andere Fall ai < ai + 1 funktioniert fast genauso.
Wir berechnen wieder die korrekte Prüfziffer der Zahenfolge c1 … c9:
c1 + 2 · c2 + … + 9 · c9 (mod 11) =
a1 + 2 · a2 + … + i · ai + 1 +
(i + 1) · ai + … + 9 · a9 (mod 11) =
b + ai - ai + 1 (mod 11)
Die Zahl b + ai - ai + 1 (mod 11) kann nur dann gleich b sein, wenn ai - ai + 1 entweder gleich 0 oder durch 11 teilbar ist. Das ist aber unmöglich, da sowohl ai als auch ai + 1 ganze Zahlen zwischen 0 und 9 sind und zusätzlich ai > ai + 1 gilt.
Ausblick: Fehlererkennende/-korrigierende Codes
ISBN ist ein Beispiel eines fehlererkennenden Codes. Diese dienen dazu, wie der Name schon sagt, um zu erkennen, dass bei der Übertragung von Daten Fehler entstanden sind. Dazu wird der eigentlichen Information (Nutzdaten) zusätzliche, eigentlich überflüssige Information (Redundanz) hinzugefügt, die dem Empfänger zur Bestimmung von Fehlern und Fehlerpositionen dient.
Im Beispiel der ISBN sind die Nutzdaten die ersten neun Ziffern und die Redundanz die Prüfziffer, mit der einzelne Tippfehler und Zahlendreher erkannt werden können. Ein weiteres Beispiel eines fehlererkennenden Codes der Informatik ist das CRC-Prüfsummen-Verfahren.
Fehlerkorrigierende Codes arbeiten nach dem gleichen Prinzip wie fehlererkennende, aber sie gestatten es zusätzlich einige Fehler zu beheben. Die Ergänzung der zu übertragenden Daten allein um eine Prüfsumme genügt nicht, um Fehlerkorrektur zu ermöglichen. Dazu ist eine geschicktere Codierung nötig. Wir können uns die Funktionsweise an folgendem Beispiel verdeutlichen.
Angenommen wir wollen einen binären Text (über 0 und 1) übertragen, also z.B. folgende Zeichenkette: 0110. Anstelle im Klartext zu übertragen, codieren wir wie folgt:
| Klartext | Codierung |
| 0 | 000 |
| 1 | 111 |
Aus dem Klartext 0110 wird also 000111111000. Der Empfänger bildet dann gemäss folgender Tabelle aus dem (eventuell gestörten) empfangenen Code wieder einen Klartext. Dieser Schritt heißt Decodierung.
| Empfangener Code | Klartext |
| 000, 001, 010, 100 | 0 |
| 111, 110, 101, 011 | 1 |
Diese Decodierungstabelle hat die Eigenschaft, dass der richtige Klartext bestimmt wird, obwohl eventuell einzelne Bits des Codes falsch übertragen wurden. Angenommen, bei der Übertragung einer codierten Null 000 wird ein einzelnes Bit falsch übertragen, also z.B. 001 anstelle 000. Gemäss obiger Decodiertabelle übersetzen wir 001 trotzdem zu einer 0.
Mit diesem Verfahren erreichen wir also einen gewissen Schutz vor Übertragungsfehlern, aber erkaufen dies durch erhöhten Übertragungsaufwand; schliesslich übertragen wir die dreifache Anzahl Bits. Eine etwas geschicktere Codierung erzielen wir, wenn wir die Bits nicht einzeln codieren, sondern immer mehrere zu einer Gruppe zusammenfassen:
| Klartext | Codierung |
| 00 | 00000 |
| 01 | 00111 |
| 10 | 11100 |
| 11 | 11011 |
Als Decodiertabelle verwenden wir diese hier:
| Empfangener Code | Klartext |
| 00000, 10000, 01000, 00100, 00010, 00001 | 00 |
| 00111, 10111, 01111, 00011, 00101, 00110 | 01 |
| 11100, 01100, 10100, 11000, 11110, 11101 | 10 |
| 11011, 01011, 10011, 11111, 11001, 11010 | 11 |
Auch diese Codierung hat die Eigenschaft, dass einzelne Bitfehler korrigiert werden können, aber das Verhältnis der Klartextlänge zur Codelänge ist 2/5 anstelle 1/3 wie bei der vorangegangenen Lösung. Dieses Verfahren ist damit (etwas) effizienter.
Es ist natürlich wünschenswert, dass nicht nur einzelne Fehler erkannt und korrigiert werden können, sondern mehrere. Dies kann durch die Einführung zusätzlicher redundanter Bits und eine geschickte Codierung erreicht werden.
Fehlerkorrigierende Codes begegnen uns übrigens im täglichen Leben. Beispielsweise wird ein solches Verfahren benutzt, um Fehler, die beim Lesen einer CD auftreten, zu korrigieren und so den Hörgenuss zu steigern. Dabei werden bei der Codierung, im Prinzip wie oben, aus dem laufenden Datenstrom jeweils 192 Bits zusammengefasst und mit 32 Fehlerkorrekturbits ausgestattet. Dieser Block wird noch geschickt weiter codiert, was wir aber hier nicht beschreiben wollen. Ein Kratzer auf der CD kann ohne weiteres die Bits eines halben Blocks beschädigen, aber durch die Codierung kann die verkratzte CD trotzdem fehlerfrei wiedergegeben werden.
Für die interessierten Leser sei abschliessend auf das Buch "Fundamentals of Error-Correcting Codes" von Huffman und Pless hingewiesen. Dieses Buch hat übrigens die ISBN 0-521-78280-5.

