Prof. Dr. Christian Scheideler, TU München
Im Mittelalter gab es noch keine Massenmedien wie Fernsehen oder Radio. Weil die meisten Leute weder schreiben noch lesen konnten, wurden Informationen überwiegend durch Mund-zu-Mund Propaganda weitergegeben, und da die Reisegeschwindigkeit der Menschen zu dieser Zeit recht begrenzt war, konnten sich Informationen höchstens mit der Geschwindigkeit von Pferden ausbreiten (obwohl spätestens seit den Kreuzzügen auch Brieftauben in unseren Breiten eingesetzt worden sind). Heutzutage ist es Dank des Telefons und neuer Medien wie Emails auch als Privatperson sehr einfach, Informationen schnell zu verbreiten. Betrachten wir dazu ein konkretes Beispiel.

Steffi hat soeben die Aufgabe bekommen, eine Jahrgangsstufenfete zu organisieren, und das wo doch gerade die Ferien angefangen haben! Jetzt muss sie versuchen, sämtliche Mitschüler über Handy oder Emails zu erreichen. Die Email-Adressen der anderen Schüler weiß Steffi zwar nicht, aber es gibt zum Glück eine Liste sämtlicher 120 Schüler in ihrem Jahrgang mit deren Telefonnummern, die jeder ihrer Mitschüler besitzt (oder hoffentlich noch besitzt!). Nun könnte Steffi natürlich 120 Telefonate führen, wozu sie allerdings weder Zeit noch Lust hat. Daher überlegt sie sich, ob es nicht auch andere Möglichkeiten gibt, möglichst schnell und einfach alle 120 Mitschüler zu erreichen.

Die erste Strategie, die ihr dabei einfällt, ist, einfach das Stille-Post-Spiel durchzuziehen. Das heißt, sie ruft einfach den ersten auf der Liste an und bittet ihn, den nächsten auf der Liste anzurufen, der dann wieder den nächsten auf der Liste anrufen soll, und so weiter, bis das Ende der Liste erreicht ist.

Der Vorteil dieses Vorgehens ist, dass jeder Schüler nur einen Anruf tätigen muss. Da diese Anrufe allerdings hintereinander durchgeführt werden müssen, kann eine erhebliche Zeitspanne verstreichen, bis alle Mitschüler informiert sind. In der Tat, wenn auch nur 10% den nächsten auf der Liste nicht am gleichen Tag anrufen oder erreichen können, dauert es mindestens 12 Tage, bis alle Schüler informiert sind. Schlimmer noch: wenn einer gar nicht reagiert, bricht das gesamte System zusammen! Steffi überlegt sich also eine andere Strategie.
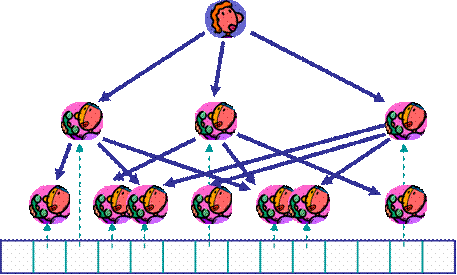
Da sie sich für Informatik interessiert und sich daher regelmäßig den Algorithmus der Woche anschaut, erinnert sie sich an die Sortiermethoden, die in der dritten Woche vorgestellt worden sind. Dort hat ein Meister zwei Gehilfen benutzt, um das Sortierproblem in zwei Teilprobleme aufzuteilen, und jeder dieser Gehilfen hat wiederum zwei Gehilfen benutzt, um diese Teilprobleme weiter zu unterteilen, und so weiter. So eine Strategie mit Gehilfen sollte sich doch auch auf Anrufe anwenden lassen! Dazu teilt Steffi die Telefonliste in zwei gleichgroße Teillisten auf. Wenn sie sich nun vornimmt, den ersten auf jeder Teilliste anzurufen, und diesen bittet, die Teilliste weiter in zwei gleichgroße Teillisten aufzuteilen und die ersten dieser Teillisten anzurufen, und so weiter, dann können ihre Mitschüler viel schneller erreicht werden.
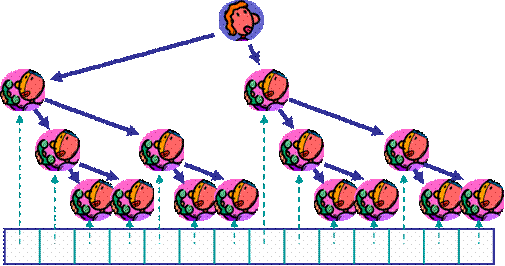
In der Tat, Steffi rechnet sich aus, dass schon nach 7 Anrufsrunden alle 120 Mitschüler informiert sind. Das ist schon wesentlich besser als 120 Anrufsrunden! Allerdings klingt das mit der Teillisteneinteilung etwas zu technisch. Ob das alle Mitschüler wirklich so mitmachen??? Sie überlegt sich also eine andere Strategie:
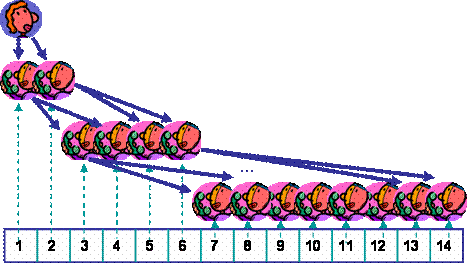
Angenommen, sie ruft die ersten beiden Mitschüler auf der Liste an, den Andi und den Berthold, und bittet Andi, die Mitschüler auf den Plätzen 3 und 4 anzurufen, und Berthold, die Mitschüler auf den Plätzen 5 und 6 anzurufen. Außerdem sollen sie die Regel weitergeben, dass jeder auf Listenplatz i die Mitschüler auf den Plätzen 2i+1 und 2i+2 anruft. Dann pflanzt sich die Information mit derselben Geschwindigkeit wie in Strategie 3 fort, aber die Anrufregel klingt nicht mehr so technisch.
Trotzdem ist Steffi noch nicht recht zufrieden mit ihrer Anrufstrategie. Was, wenn sich einer der Mitschüler verzählen sollte und ein falsches Paar Schüler auf der Liste anruft? Außerdem kann es natürlich ein paar Schlafmützen geben, die einfach vergessen, die nächsten auf der Liste anzurufen. Dann würden einige Mitschüler nicht informiert werden, die dann natürlich sauer auf Steffi wären!
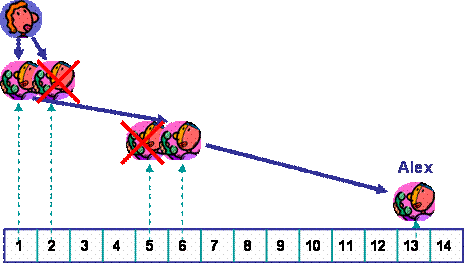
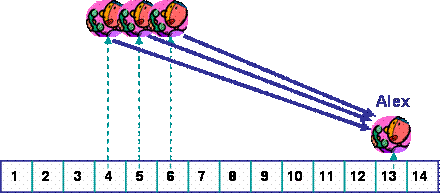
Steffi überlegt sich also die Strategie, dass jeder auf Listenplatz i die Mitschüler auf den Plätzen 2i+1 bis 2i+4 anruft. Dann wird im Idealfall jeder Schüler von genau zwei Mitschülern angerufen. Solange also für jeden auf der Liste höchstens einer von den beiden Mitschülern, die ihn anrufen sollen, nicht erreichbar ist (oder einen Fehler macht, oder den Anruf schlichtweg verpennt), werden alle Schüler, die erreichbar sind, informiert. Das kann man sich anschaulich so überlegen: wenn man für jeden Schüler einen Vorgänger wählt, der ordentlich arbeitet, dann bekommt man für jeden eine ununterbrochene funktionierende Kette bis zum Anfang - Steffi.
Steffi überlegt sich, dass diese Strategie vielleicht noch ein wenig robuster ausgelegt werden sollte, damit sie wirklich sicher sein kann, dass auch alle erreicht werden. Sie überlegt sich dazu folgendes: wenn jeder Schüler auf Listenplatz i die Mitschüler auf den Plätzen 2i+1 bis 2i+2r für eine feste Zahl r anruft, dann wird im Idealfall jeder Schüler von r anderen Schülern angerufen. Dann können beliebige r-1 der r Schüler Probleme machen, und alle erreichbaren Mitschüler werden immer noch erreicht!
Hier ist ein guter Zeitpunkt gekommen, mal ein paar Experimente durchzuführen, um die folgende Frage zu beantworten. Wie groß muss Steffi das r wählen, damit alle erreichbaren Schüler mindestens mit einer Wahrscheinlichkeit p benachrichtigt werden, wenn es insgesamt x problematische Schüler gibt, die zufällig über die Listenplätze verteilt sind? Um das herauszufinden, kann man folgenden Algorithmus als Grundlage verwenden.
Algorithmus r-faches Broadcasting:
- Datenstruktur: ein Array A[1..N], wobei A[i] die Anzahl der Anrufe zählt, die der Schüler auf Platz i bekommen hat.
- Für alle zuverlässigen Schüler wird A[i] auf 0 gesetzt.
- Für alle unzuverlässigen Schüler wird A[i] auf -(r+1) gesetzt (damit sie auch bei r Anrufen nicht auf einen Wert ≥ 0 kommen)
Bei dieser ganzen Überlegerei hat Steffi so langsam richtig Spaß daran bekommen, sich Strategien auszudenken. Sie stellt sich jetzt erschwerend die Situation vor, dass zwar jeder Schüler die Telefonnummern aller Mitschüler der Jahrgangstufe kennt, es aber keine einheitliche Liste gibt, so dass die Strategien mit den Listenplätzen oben nicht anwendbar sind. Gibt es dann immer noch ein schnelles und robustes Verfahren, um alle Schüler zu erreichen, selbst wenn, sagen wir, ein beliebiges Viertel der Schüler unzuverlässig ist?
Nach einigem Nachdenken kommt Steffi auf die Idee, dass sowohl Steffi als auch jeder zum ersten Mal angerufene Schüler einfach r zufällig gewählte Mitschüler anruft.
Wenn Steffi mit dieser Strategie anfängt, dann informiert sie garantiert r noch nicht angerufene Mitschüler, falls diese erreichbar sind. Im Idealfall sind alle zuverlässig und rufen dann jeweils r weitere zufällig ausgewählte Schüler aus, so dass im Idealfall r2 noch nicht angerufene Mitschüler erreicht werden. In Wirklichkeit kann es dabei natürlich zu Überschneidungen kommen. Außerdem können bereits angerufene Schüler oder unzuverlässige Schüler angerufen werden, was der Ausbreitung angerufener Schüler schadet. Trotzdem kann man aber durch Experimente sehen, dass sich Steffis Infomationen schon bei relativ kleinem r mit hoher Zuverlässigkeit schnell ausbreiten. Dafür können wir den folgenden Algorithmus verwenden.
Algorithmus r-faches zufälliges Broadcasting:
- A[1..N]: Array, in dem anfangs A[i]=-1 ist, wenn der Schüler i unzuverlässig ist, und A[i]=0 ist, wenn der Schüler i zuverlässig ist
- Wenn ein zuverlässiger Schüler auf Platz i zum ersten Mal angerufen wird, wird A[i] auf 1 gesetzt, und sobald er alle seine Anrufe erledigt hat, wird A[i] auf 2 gesetzt.
- C[0..N][1..r]: Array, in dem C[i][j] den Listenplatz des j. Schülers angibt, den der Schüler auf Platz i anruft (Steffi zählt hier als Schüler 0).
Natürlich kann man sich noch jede Menge anderer Broadcasting-Strategien
ausdenken, und jeder sei an dieser Stelle ermuntert, diese mal zu
testen. Welche Strategie hättet ihr denn an Stelle von Steffi
gewählt?


