Michael Behrisch, Humboldt-Universität zu Berlin
Amin Coja-Oghlan, Humboldt-Universität zu Berlin
Peter Liske, Humboldt-Universität zu Berlin
 ).
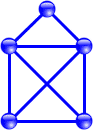
Ein schönes Beispiel dafür ist das „Haus vom Nikolaus“
(oder besser: Haus des Nikolaus`):
).
Ein schönes Beispiel dafür ist das „Haus vom Nikolaus“
(oder besser: Haus des Nikolaus`):
Dabei handelt es sich um eine Figur aus fünf Knoten (die dicken Punkte) und acht Kanten (die Linien, die je zwei Knoten miteinander verbinden). Kann man die linksstehende Figur zeichnen, ohne den Stift abzusetzen und ohne eine Linie doppelt zu ziehen?
Zwar hat sich die Lösung ziemlich schnell rumgesprochen (zumal es sogar 44 verschiedene Lösungen gibt). Aber zum Glück gibt es andere schöne Figuren, die man auch in einem Zug zeichnen kann – wenn man weiß, wie es geht:
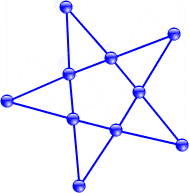
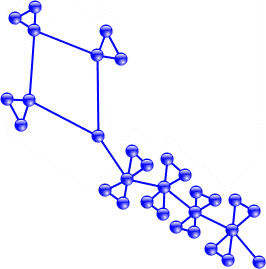
Stern und Drachen
Bei manch anderen Figuren muss man vielleicht ziemlich lange probieren – um am Ende festzustellen, dass es gar nicht geht:

Wir wollen uns hier einen Algorithmus ansehen, der eine Figur immer
in einem Zug zeichnet, wenn das möglich ist.
Dazu beschäftigen wir uns zunächst nur mit Figuren, die man derart
in einem Zug durchzeichnen kann, dass am Ende der Stift wieder an dem
Ausgangspunkt ankommt.
Den Weg, den der Stift dabei zurücklegt, nennt man eine Eulertour,
denn die Frage, wann man eine Figur ohne abzusetzen zeichnen kann, wurde
erstmals von dem Mathematiker Leonhard Euler im Zusammenhang mit dem
so genannten Königsberger Brückenproblem (siehe
untenstehende Links)
beantwortet.
Wir werden im folgenden sehen, warum man beispielsweise den
Stern mit einer Eulertour zeichnen kann, das Schiff und das Nikolaushaus
jedoch nicht. Hierzu ist es wichtig, sich die Knoten der Figur anzuschauen,
das sind diejenigen Stellen, an denen der Stift die Richtung wechseln kann (in
den Bildern als dicke Punkte gezeichnet).
Wann gibt es überhaupt eine Eulertour?
Der Grad eines Knotens ist die Anzahl der Linien, die sich dort treffen;
z.B. ist der Grad der Mastspitze des Schiffes 3.
Wenn man eine Figur so in einem Zug zeichnet, dass Start- und Endpunkt
übereinstimmen und keine Kante mehr als einmal benutzt wird,
dann führt man den Stift dabei natürlich in jeden Knoten genau so
oft hinein, wie man ihn auch wieder hinausführt.
Das bedeutet: der Grad jedes Knotens muss eine gerade Zahl
sein.
Aber das Schiff hat sogar vier Knoten mit ungeradem Grad (alle am Segel).
Deshalb ist es unmöglich, diese Figur in einem Zug mit gleichem Start-
und Endpunkt zu zeichnen.
(Dies gilt auch für das „Haus vom Nikolaus“, weil es in
dieser Figur zwei Knoten mit Grad 3 gibt.)
Andererseits haben beim Stern alle Knoten geraden Grad.
Gibt es in allen solchen Figuren eine Eulertour?
Falls ja, wie
können wir eine finden?
Wie man eine Eulertour erstellt
 Wenn einem nichts besseres einfällt, könnte man einfach
irgendwo anfangen und „draufloszeichnen“.
Wir beginnen dabei an einem beliebigen Knoten und folgen von dort irgendeiner
Kante, sodass wir einen neuen Knoten erreichen.
Dort folgen wir wieder einer Kante zu einem neuen Knoten, und so weiter.
Wir dürfen dabei allerdings jede Kante nur ein Mal benutzen.
Wenn einem nichts besseres einfällt, könnte man einfach
irgendwo anfangen und „draufloszeichnen“.
Wir beginnen dabei an einem beliebigen Knoten und folgen von dort irgendeiner
Kante, sodass wir einen neuen Knoten erreichen.
Dort folgen wir wieder einer Kante zu einem neuen Knoten, und so weiter.
Wir dürfen dabei allerdings jede Kante nur ein Mal benutzen.
Jedesmal, wenn wir einen Knoten betreten und verlassen haben,
können wir zwei seiner Kanten nun nicht mehr benutzen.
Hatte der Knoten vor dem Betreten eine gerade Anzahl von verfügbaren Kanten,
so hat er nachher ebenso eine gerade Anzahl.
Es kann uns also nicht passieren, dass wir in einer Sackgasse stecken bleiben.
Daher werden wir früher oder später mit unserer
„Drauf-los“-Strategie wieder im Ausgangsknoten ankommen.
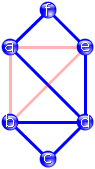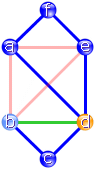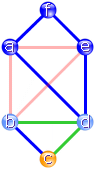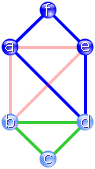
Im Bild links ist dabei ein „Kreis“ (d.h. ein Weg über
mehrere Kanten, der am Ausgangspunkt ankommt) mit drei Kanten entstanden. Die
durchlaufenen Knoten sind b, e und a.
 Meistens gelingt es so aber noch nicht, die ganze Figur zu zeichnen, da noch
einige Kanten übrigbleiben. Wir sind also beim Einzeichnen des Kreises an
irgendeiner Stelle „falsch abgebogen“ und haben
dadurch einen Teil der Figur ausgelassen.
Deshalb müssen wir versuchen, den Kreis, den wir schon
eingezeichnet haben, noch zu „erweitern“.
Dies geht zum Beispiel, indem man vom Start- / Zielknoten des schon erstellten
Kreises nochmals losläuft.
Dabei erhalten wir einen weiteren Kreis. Im Beispiel ist dies ein grünes
Dreieck zwischen b, d und c (rechtes Bild).
Die beiden Kreise können wir nun zu einem längeren zusammenfügen.
Aber damit sind wir immer noch nicht fertig. Die Kanten vom Startknoten sind
nun verbraucht, von diesem Knoten geht es also nicht weiter.
Meistens gelingt es so aber noch nicht, die ganze Figur zu zeichnen, da noch
einige Kanten übrigbleiben. Wir sind also beim Einzeichnen des Kreises an
irgendeiner Stelle „falsch abgebogen“ und haben
dadurch einen Teil der Figur ausgelassen.
Deshalb müssen wir versuchen, den Kreis, den wir schon
eingezeichnet haben, noch zu „erweitern“.
Dies geht zum Beispiel, indem man vom Start- / Zielknoten des schon erstellten
Kreises nochmals losläuft.
Dabei erhalten wir einen weiteren Kreis. Im Beispiel ist dies ein grünes
Dreieck zwischen b, d und c (rechtes Bild).
Die beiden Kreise können wir nun zu einem längeren zusammenfügen.
Aber damit sind wir immer noch nicht fertig. Die Kanten vom Startknoten sind
nun verbraucht, von diesem Knoten geht es also nicht weiter.
 Aber: wenn wir die Kanten, die wir schon nachgezeichnet haben, aus der Figur
löschen, haben immer noch alle Knoten geraden Grad. Deshalb können
wir auf dem übriggebliebenen Teil wieder einen neuen Kreis
finden: wir suchen uns dazu einen Knoten auf unserem
„alten“ Kreis, der eine Kante hat, die wir noch nicht
nachgezeichnet haben. Von diesem Knoten aus zeichnen wir wieder drauf los, bis
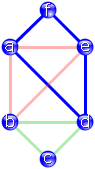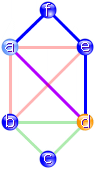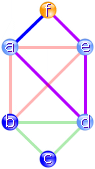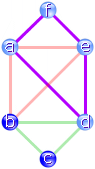
wir einen neuen Kreis eingezeichnet haben. Im Beispiel erhalten wir das
Viereck mit den Eckpunkten a, d, e und f
(mit lila Kanten dargestellt, linkes Bild).
Aber: wenn wir die Kanten, die wir schon nachgezeichnet haben, aus der Figur
löschen, haben immer noch alle Knoten geraden Grad. Deshalb können
wir auf dem übriggebliebenen Teil wieder einen neuen Kreis
finden: wir suchen uns dazu einen Knoten auf unserem
„alten“ Kreis, der eine Kante hat, die wir noch nicht
nachgezeichnet haben. Von diesem Knoten aus zeichnen wir wieder drauf los, bis
wir einen neuen Kreis eingezeichnet haben. Im Beispiel erhalten wir das
Viereck mit den Eckpunkten a, d, e und f
(mit lila Kanten dargestellt, linkes Bild).
Wir haben nun einen „alten“ Kreis und einen „neuen“, der an irgendeinem Knoten des alten Kreises beginnt und endet. Die Idee ist, den neuen Kreis in den alten „einzuhängen“, um einen längeren Kreis zu erhalten. Dazu folgen wir zunächst dem ersten Kreis bis zu der Stelle, an der wir den zweiten Kreis begonnen haben. Von dort an folgen wir dem zweiten Kreis, bis wir wieder an dessen Ausgangspunkt sind. Schließlich setzen wir den ersten Kreis fort bis zu Ende.
Wir haben jetzt also die beiden „kleinen“ Kreise vereinigt und daraus einen „größeren“ Kreis gebastelt. Leider deckt auch der „größere“ Kreis noch immer nicht die ganze Figur ab. Aber was spricht dagegen, das Verfahren einfach zu wiederholen?
Also: wir suchen uns einen Knoten auf unserem „größeren“ Kreis, von dem eine Kante ausgeht, die wir noch nicht besucht haben. Dann finden wir in der Figur, aus der der „größere“ Kreis gelöscht ist, einen neuen Kreis und verknüpfen diesen mit dem „alten“ Kreis wie vorher. Das wiederholen wir, bis alle Kanten der Figur verbraucht sind. Auf diese Weise bekommen wir eine Eulertour.
Die erste Teiltour im Beispiel war also
(b,e,a,b), die zweite
(b,d,c,b) und die dritte
(a,d,e,f,a).
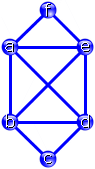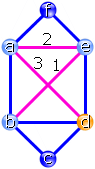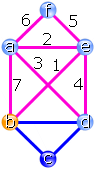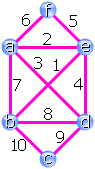
Zusammengeklebt ergibt sich:
(b,e,a,d,e,f,a,b,d,c,b),
wie im rechten Bild angedeutet.
Der Algorithmus
Der Algorithmus geht ganz ähnlich vor wie im obigen Beispiel, nur dass er das Zusammenkleben sofort erledigt. Das heißt, nachdem eine Teiltour gefunden wurde (z.B. (b,e,a,b,d,c,b)), wird die nächste gleich an Ort und Stelle eingefügt, also angenommen Tour = (b,e,a,b,d,c,b) und u = a, dann könnte die gewählte Kante (a,d) sein und so die Tour vorläufig zu (b,e,a,d,b,d,c,b) erweitert werden. Dies ist natürlich noch keine gültige Tour, aber der Algorithmus fährt ja auch fort bis er wieder bei a ankommt.
Bisher haben wir uns nur mit Figuren beschäftigt, die eine Eulertour haben, d.h. die so in einem Zug gezeichnet werden können, dass Start- und Endpunkt übereinstimmen. Wie wir schon wissen, funktioniert das aber nur, wenn alle Knoten in der Figur geraden Grad haben. Leider trifft das auf das „Haus vom Nikolaus“ nicht zu: die beiden unteren Knoten haben Grad 3. Trotzdem kann man die Figur in einem Zug zeichnen, nur eben nicht mit gleichem Start- und Endpunkt.
Wie können wir also unseren Algorithmus anpassen, so dass er auch für das „Haus vom Nikolaus“ funktioniert?
Das Haus vom Nikolaus
 Ein einfacher Trick ist, einen neuen Knoten einzubauen und ihn mit den beiden
Knoten vom Grad 3 zu verbinden: In dieser Figur haben alle Knoten geraden
Grad, deshalb funktioniert der Algorithmus und liefert uns eine Eulertour.
Ein einfacher Trick ist, einen neuen Knoten einzubauen und ihn mit den beiden
Knoten vom Grad 3 zu verbinden: In dieser Figur haben alle Knoten geraden
Grad, deshalb funktioniert der Algorithmus und liefert uns eine Eulertour.
Zum Schluss lassen wir einfach in dieser Eulertour den „künstlich
eingebauten“ Knoten weg: Wir beginnen den Weg mit seinem linken
„Nachbarknoten“ und hören bei seinem rechten Nachbarn auf
– und bekommen eine Lösung für das „Haus vom Nikolaus“!
Dieser Trick funktioniert immer dann, wenn die Figur, die wir zeichnen wollen, genau zwei Knoten von ungeradem Grad hat. Aber andere Figuren (mit mehr als zwei Knoten von ungeradem Grad) können gar nicht in einem Zug gezeichnet werden, selbst wenn man erlaubt, dass Start- und Zielknoten verschieden sind.
Von Postboten und der Müllabfuhr
Abgesehen davon, dass man mit dem beschriebenen Algorithmus seine Mitschüler beeindrucken kann (insbesondere damit, dass man schon durch „Draufschauen“ und schnelles Testen der Grade der Knoten entscheidet, ob sich eine Figur in einem Strich zeichnen lässt), gibt es auch in der Praxis Anwendungen. Nimmt man zum Beispiel an, dass die Kanten Straßen sind und die Knoten Kreuzungen, so ist ein Weg, der alle Straßen genau einmal durchläuft, gerade eine Eulertour. Wenn ein Straßennetz Eulertouren hat, stellen diese schnelle und benzinsparende Routen für die Postzustellung und die Müllabfuhr dar. Unser Algorithmus findet solche Touren auf einfache Weise. (Für Netze mit Hunderten von Straßen übernimmt natürlich ein Computer die Arbeit.)
Tatsächlich gibt es in Städten aber mehr als zwei Kreuzungen mit einer ungeraden Zahl von Straßen. Dadurch muss bei der Planung der Müllbeseitigung berücksichtigt werden, dass einige Straßen mehrfach genutzt werden. Dabei spielt auch die Länge der Straßen eine Rolle, was zum so genannten Briefträgerproblem (Chinese Postman Problem) führt.
- Leonhard Euler und das Königsberger Brückenproblem in der Wikipedia
- Graphenspiele mit Eulertouren
- Eulerkreise und Nikolaushäuser in der Wikipedia (man beachte auch das Briefträgerproblem)
- Eulerkreismaterial für eine Unterrichtseinheit in der vierten oder fünften Klasse
- Eulertour bei der Müllabfuhr

