Wolfgang P. Kowalk, Universität Oldenburg
Schon wieder Aufräumen, dabei habe ich doch erst neulich... Nun ja, wenn alles durcheinander liegt, dann lohnt es sich vielleicht doch, mal eben Ordnung zu schaffen; man findet alles schneller wieder. Lass uns also mal die Bücher auf dem Regal nach ihren Titeln sortieren, so dass man jedes gleich zur Hand hat, wenn man es braucht.
Doch wie schafft man am schnellsten Ordnung? Die folgende Idee scheint
sehr natürlich zu sein. Wir bringen alle Bücher von links
nach rechts im Regal fortschreitend an die richtige Position. Das
erste Buch bleibt zunächst an seinem Platz; dann nehmen wir das
zweite Buch hinzu und vertauschen es mit dem ersten, falls es links
von diesem stehen muss; dann nehmen wir das dritte Buch hinzu,
vertauschen es mit dem zweiten, falls nötig, und vertauschen es
anschließend gegebenenfalls mit dem ersten. Dann nehmen wir das
vierte Buch hinzu, usw. Allgemein nehmen wir also an, das alle Bücher
links im Bücherregal bereits sortiert sind; sodann nehmen wir
eines hinzu und bringen es durch Vertauschen mit dem linken Nachbarn
an die richtige Position.
Statt der Buchtitel schreiben wir im folgenden Nummern, weil der Algorithmus dann einfacher zu erklären ist.
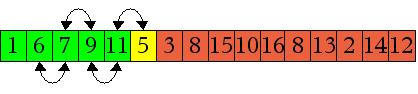In dem Bild sind die linken fünf Bücher bereits sortiert; wird
das Buch mit der Nummer 5 hinzu genommen, so steht es offensichtlich
falsch. Also vertauschen wir es zunächst mit dem Buch mit der
Nummer 11, dann mit dem mit der Nummer 9 usw. bis es einmal rechts
vom Buch mit der Nummer 1 an seiner richtigen Position steht. Dann
fahren wir mit dem Buch mit der Nummer 3 fort, usw. Offenbar kommen
dadurch alle Bücher einmal an ihren richtigen Platz.
Wie kann man so etwas jetzt programmieren? Das folgende Programm macht das! Es benutzt ein sogenanntes Feld von Zahlen; in der Informatik sagt man dazu Array. Die Werte in einem Array werden durch einen Zahlenwert ausgewählt, der auch als Index bezeichnet wird. Unter A[i] versteht man den Wert an der i-ten Stelle, oder den Wert unter dem Index i. In der Mathematik würde man statt dessen Ai schreiben, was genau das gleiche bedeutet. Die Werte stehen also in einem Feld der Länge n und werden mit A[1], A[2], ..., A[n-1], A[n] bezeichnet.
Die Funktion SortiereDurchEinfuegen sortiert das
Array "A" mit n Elementen (z.B. Büchern) von klein nach groß.
SortiereDurchEinfuegen(A)
| Anzahl
verschobener Bücher von 1 bis n-1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Runden des Algorithmus von 1 bis n |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
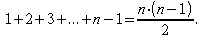
Diese Formel lässt sich leicht anhand des nebenstehenden Bildes einsehen. Es gibt in dem Rechteck n·(n-1) Felder, und davon wird gerade die Hälfte für das Vergleichen und Vertauschen verwendet. Allerdings ist unser Algorithmus im Mittel immer schneller als der schlechteste Fall, da bei zufälliger Anordnung der Bücher nur etwa die Hälfte der Vergleichs- und Schiebeoperationen nötig sind.
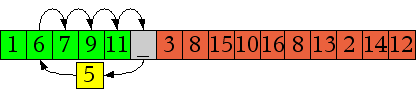Sicherlich hast du schon bemerkt, dass unser Sortierverfahren sehr umständlich
ist, weil wir benachbarte Bücher immer vertauschen. Sobald wir
wissen, wo das neue Buch hingehört, schieben wir alle größeren
Bücher um eine Stelle nach rechts und stellen das neue Buch an
die richtige Stelle. Statt zwei Bücher k-mal zu
vertauschen, verschieben wir (k+1)-mal
ein Buch, was offenbar weniger aufwändig ist, weil einmal
Vertauschen drei Verschiebeoperationen benötigt. Das
spart eine ganze Menge Arbeit und Zeit!
Nun könnten wir auf die Idee kommen, dass das Verschieben einer “beliebigen” Anzahl von Büchern nach rechts nur einen einzigen Schritt erfordert: Wir drücken einfach die ganze Reihe von Büchern um eine Position nach rechts. Im Computer ist das aber nicht so einfach möglich. Hier müssen die Objekte (Bücher) wirklich einzeln nacheinander nach rechts geschoben werden, um eine freie Stelle für das einzufügende Objekt (Buch) zu schaffen.
Man kann die Bearbeitungszeit noch weiter verringern, wenn man die
Einfügestelle schneller findet, denn das ständige
Vergleichen kostet ja auch Zeit. Nun sind die ersten Bücher ja
schon sortiert. Statt vom letzten der sortierten Bücher bis zum
ersten alle zu vergleichen, guckt man erst mal in der Mitte nach (im
letzten Bild in der Mitte des Intervals [1,11]). Liegt die
Einfügestelle jetzt links von dem mittleren Buch, so suche in
dem Intervall [1,6], sonst in der rechten Hälfte [7,11] usw. Man
nennt dieses Verfahren binäres Suchen, weil man den
Suchbereich ständig halbiert (binär bedeutet
zweiwertig, also in zwei Teile teilen). Hat man die
Einfügestelle gefunden, so schiebt man alle Bücher ab
dieser Stelle um eine Position nach rechts und kann dann das neue
Buch an die richtige Position stellen. Man zeigt leicht, dass auf
diese Weise das Finden der Einfügestelle logarithmisch mit der
Anzahl der Bücher wächst. Selbst bei Tausend Büchern
bräuchte man nicht mehr als zehn Schritte, um die Einfügestelle
zu finden, und das ist schon ziemlich gut.
Wie du siehst, kann das Sortieren sehr schnell erledigt werden, wenn man nur den richtigen Algorithmus verwendet. Daher ist es in der Informatik so wichtig, den richtigen Algorithmus zu kennen und einzusetzen, weil der richtige Algorithmus u.U. ein Problem erst lösbar macht. Wenn du weitere Verbesserungen dieses Algorithmus kennenlernen willst, oder wenn du die verschiedenen Algorithmen animiert ablaufen lassen willst, so gehe doch einmal auf die unten angegebene Web-Site.