Prof. Dr. Ulrik Brandes, Universität Konstanz
Dipl.-Math. Gabi Dorfmüller, Universität Konstanz
Wichtig, Wichtiger, am Wichtigsten
Du hast sicherlich schon einmal die Suchmaschine Google verwendet, um beispielsweise Informationen für ein Referat über eine momentan unvermeidliche Sportart zu finden. Auf die Anfrage "fußball" erscheint folgende Liste von Dokumenten:

Aber hast Du Dir auch schon mal überlegt, wie Google eigentlich funktioniert? Wer entscheidet, welche Quellen an oberster Stelle erscheinen?
Das World Wide Web (WWW) ist ein Netzwerk aus Milliarden von Dokumenten. Das sind vor allem so genannte Web-Seiten, die durch Links (Verweise) miteinander verknüpft sind. Google verwendet einen speziellen Algorithmus, um den Dokumenten eine Relevanz (Wichtigkeit) zuzuordnen. Ein zentraler Teil des Algorithmus' ist die Auswertung der Links. Dieser Baustein wird auch als PageRank bezeichnet und ist unser Algorithmus der Woche.
Zur Einstimmung gucken wir uns noch einmal die Verlinkungen von Wikipedia-Einträgen aus dem 5. Algorithmus der Woche an.
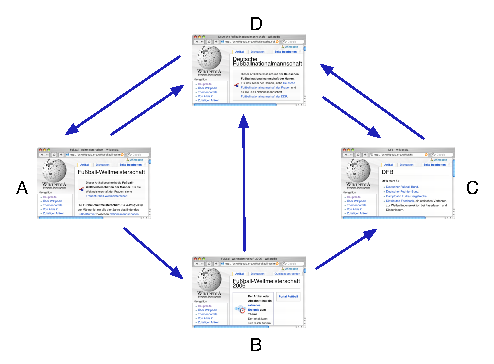
Ein Internet-Surfer bewegt sich durch ein solches Netzwerk, indem er auf irgendeiner Seite startet und dann jeweils auf einen der darin enthaltenen Links klickt, um zur nächsten zu gelangen. Wenn Du folgendes Experiment mit 10 oder mehr Personen (z.B. Deiner Schulklasse) durchführst, kannst Du beobachten, dass man aus dem Verhalten von Internet-Surfern etwas lernen kann.
Haben die Wenigsten auf der Seite ganz unten (B) angehalten? Das ist wahrscheinlich, denn abhängig davon, wie gut eine Seite verlinkt ist, kommt man mit größerer Häufigkeit an ihr vorbei. Google verwendet deshalb die Erreichbarkeit einer Seite, um ihre Wichtigkeit im WWW festzulegen. Eine Seite, zu der Internet-Surfer häufig hingeführt werden, taucht auch weiter oben in der Ergebnisliste auf.
Aber wie kommt man an solche Werte, ohne dass eine riesige Anzahl von Surfern losgeschickt werden muss? Man kann sie berechnen, und das ist gar nicht mal kompliziert.
Man muss sich nämlich nur überlegen, wie ein Surfer überhaupt zu einer Seite hingelangen kann. Wer z.B. im obigen Beispiel auf Seite C ist, war vorher entweder auf Seite B oder auf Seite D, hätte von beiden aber auch woanders hingehen können. Wenn wir davon ausgehen, dass bei mehreren möglichen Links von diesen einer zufällig gewählt wird, dann kann man daraus ein Gleichungssystem für die Besuchshäufigkeiten der Web-Seiten herleiten:

In der letzten Gleichung steht zum Beispiel, dass die Häufigkeit d, auf Seite D zu landen, sich aus den Besuchshäufigkeiten a, b und c der Seiten A, B und C ergibt (weil man von allen nach D gelangen kann). Der Faktor 1/2 vor a und b bedeutet dabei, dass nur in der Hälfte der Fälle der Link von A oder B nach D benutzt wird (und sonst der von A nach B bzw. der von B nach C).
Du kannst sicher nachrechnen, dass

eine Lösung des Gleichungssystems ist. Es gibt zwar unendlich viele Lösungen, aber weil sich jede andere durch Multiplikation aller vier Werte mit demselben Faktor ergibt, ist b immer nur halb so groß wie der zweitkleinste Wert a. Deshalb waren wir uns auch so sicher, dass beim Experiment die Wenigsten auf B stoppen würden.
Ganz so leicht ist es dann aber doch nicht, denn wir haben oben einen Teil des Beispiels aus der 5. Woche weg gelassen.

Folgt man hier dem roten Link von D nach F, steckt man in einer Sackgasse. Es könnte auch sein, dass es von F zwar weiter zu anderen Seiten, aber nicht wieder zurück nach A—E geht. Seiten, zu denen man irgendwann nicht mehr zurück kehren kann, führen zu Lösungen, die für die Sortierung ungeeignet sind (warum wohl?).
Das im Experiment nachgeahmte Surf-Verhalten entspricht aber ja sowieso nicht dem realen. Wer auf einer Seite keinen interessanten Link findet, wird irgend eine andere Seite aufrufen (z.B. durch den "Zurück"-Knopf, die Favoriten oder die direkte Eingabe der Adresse).
Das Gleichungssystem wird dadurch nur wenig komplizierter. Wir legen einfach fest, dass zum Beispiel in einem von fünf Fällen kein Link verfolgt, sondern direkt zu einer Seite gesprungen wird, und dass beim Springen keine Seite bevorzugt wird (d.h. bei sechs Seiten wird jede in ungefähr einem von sechs Fällen angesprungen). Damit bleibt jede Seite zu jedem Zeitpunkt erreichbar, und wir kommen von jeder Seite auch wieder weg.
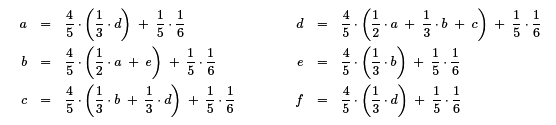
Dieses Gleichungssystem zu lösen ist auch nicht viel schwieriger. Wir sind aber trotzdem noch nicht fertig, denn das Netzwerk, das eine Internet-Suchmaschine auswerten muss, führt zu einem Gleichungssystem mit Millarden von Unbekannten und Gleichungen. Das schaffen auch schnelle Computer nicht durch Auflösen und Einsetzen wie Du es in der Schule lernst.
Glücklicherweise hat das Gleichungssystem einige Eigenschaften, die man gut ausnutzen kann, wenn man die genaue Lösung gar nicht benötigt. Ein ganz einfacher Algorithmus kann nämlich sehr schnell ein ausreichend gutes Ergebnis berechnen. Wir haben ja für jede Unbekannte eine Gleichung; sind alle anderen Unbekannten schon bestimmt, brauchen wir sie nur noch in die eine übrige Gleichung einzusetzen. Der Algorithmus beginnt daher mit beliebigen Werten (z.B. 1) für eine Lösung, und rechnet für jede Unbekannte aus, was ihr richtiger Wert wäre, wenn alle anderen schon stimmten. Mit den so erhaltenen neuen Werten wird das Gleiche nochmal gemacht. Und nochmal. Und nochmal. Und so weiter und so fort.
Mit jedem Schritt werden die Werte ein bißchen besser, und wenn sich kaum noch was ändert, ist das ein Zeichen dafür, dass man schon nahe an der richtigen Lösung ist.
| 1.Schritt | 2.Schritt | 3.Schritt | ... | 21.Schritt | 22.Schritt | ... | Lösung | |
|---|---|---|---|---|---|---|---|---|
| a | 1.00000 | 0.30000 | 0.43333 | ... | 0.08488 | 0.08478 | ... | 0.08454 |
| b | 1.00000 | 1.23333 | 0.39333 | ... | 0.11962 | 0.11950 | ... | 0.11926 |
| c | 1.00000 | 0.56667 | 0.76222 | ... | 0.11681 | 0.11668 | ... | 0.11634 |
| d | 1.00000 | 1.50000 | 0.93556 | ... | 0.19292 | 0.19292 | ... | 0.19203 |
| e | 1.00000 | 0.30000 | 0.36222 | ... | 0.06527 | 0.06523 | ... | 0.06514 |
| f | 1.00000 | 0.30000 | 0.43333 | ... | 0.08488 | 0.08478 | ... | 0.08454 |
Mit diesem Wissen müsstest Du eigentlich folgende Frage beantworten können: Wenn ich meine eigene Homepage von all meinen Freunden verlinken lasse, erscheint sie dann bei Google ganz oben? Antwort
Es gibt viele Möglichkeiten, Wichtigkeit in einem Netzwerk aus verlinkten Seiten zu definieren und beim Anordnen der Treffer zu berücksichtigen. Außerdem kann man die Häufigkeit der Sprünge unterschiedlich festlegen und die Auswahl der direkt angesprungenen Seiten beeinflussen. Auch wenn die Details ein Geheimnis sind, scheint es bei Google recht gut zu funktionieren.
- Prof. Dr. Ulrik Brandes
- Dipl.-Math.Gabi Dorfmüller
- PageRank-Eintrag in der Wikipedia
- visone – Ein Programm mit dem man Netzwerke eingeben und z.B. PageRank berechnen kann.

