Autor
Friedrich Eisenbrand, Universität Dortmund
Heute behandeln wir den ältesten bereits aus Aufzeichnungen aus der Antike bekannten Algorithmus. Er wurde ca. 300 v. Chr. von Euklid in seinem Buch Die Elemente beschrieben.
Stell Dir vor, du hast zwei Stäbe der Länge a und b, wobei a und b ganze Zahlen sind. Du möchtest die Stäbe in gleichgroße Stücke zersägen und zwar so, dass die Länge d der Stücke so groß ist wie möglich.
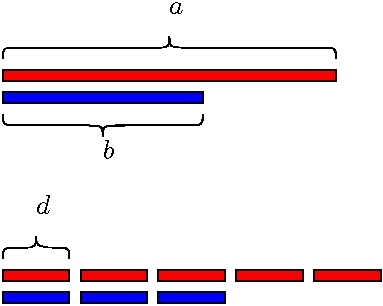
Unser Algorithmus der Woche berechnet diese gesuchte Länge d. Der Algorithmus hat zwei Versionen. Die erste Version ist langsam, die zweite ist schnell.
Die Zahlen a/d und b/d sind natürliche Zahlen, nämlich jeweils die Anzahl der Stücke, in die die Stäbe zerschnitten werden. In dem Bild oben lässt sich der längere Stab in 5 Stücke der Länge d zerteilen und der kürzere in 3.
Wie finden wir nun die gesuchte Länge d? Wenn beide Stäbe gleich lang sind, dann ist die gesuchte Länge d sofort klar. Es ist die gemeinsame Länge beider Stäbe, wir müssen also die Stäbe nicht zersägen.
Nehmen wir also an, dass die Stäbe unterschiedliche Längen haben, wobei a größer ist als b.

Beim Nebeneinanderlegen beider Stäbe fällt Dir etwas auf! Wenn beide Stäbe sich in Stücke der Länge d aufteilen lassen, dann können wir von dem längeren Stab ein Stück abschneiden, das genauso lang ist wie der kürzere Stab.
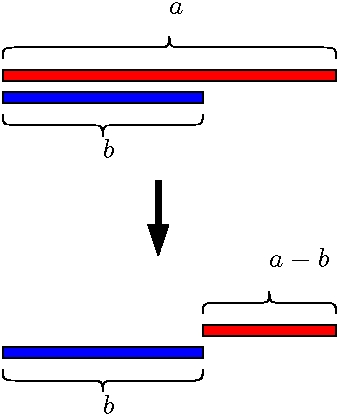
Der neue Stab hat jetzt die Länge a-b und lässt sich ebenfalls exakt in Stücke der Länge d zersägen. Umgekehrt gilt: Wenn sich der neue Stab und der Stab der Länge b in Stücke der Länge d zerteilen lassen, dann lässt sich auch der alte Stab der Länge a in Stücke der Länge d zerteilen.
Das wichtige Prinzip (P) ist also kurz das folgende:
- Wenn a=b, dann ist die gesuchte Länge a.
- Wenn a größer ist als b, dann ist die gesuchte Länge für a und b dieselbe wie die gesuchte Länge für a-b und b.
Wir können jetzt einen Algorithmus aufschreiben, der uns die gesuchte Länge berechnet.
LangsamEuklid
| 1 |
| 2 |
Wir müssen uns an dieser Stelle fragen, ob unser Algorithmus fertig wird und nicht immer weiter die Stäbe in kleinere Stücke zersägt und nie aufhört. Hierzu kann man folgendes beobachten. Wir beginnen mit zwei Stäben, deren Längen jeweils natürliche Zahlen a und b sind. Während der Algorithmus läuft, bleiben die Längen natürliche Zahlen. Insbesondere ist die Länge der beiden Stäbe immer mindestens 1. Da einer der Stäbe in jeder Runde um mindestens eins gekürzt wird, endet der Algorithmus schließlich nach höchstens a+b Runden.
Die gesuchte Länge d ist, so wie a und b, auch eine natürliche Zahl. Es ist eine natürliche Zahl, die sowohl a als auch b teilt. Mathematisch ausgedrückt bedeutet dies, dass es natürliche Zahlen x und y gibt mit d· x =a und d · y = b. In unserer Anschauung ist x die Anzahl der Stücke, die wir aus dem Stab der Länge a schneiden und y ist die Anzahl der Stücke, die wir aus dem Stab der Länge b schneiden.
Die Zahl d ist der größte gemeinsame Teiler von a und b, denn nach dem Prinzip (P) ist der größte gemeinsame Teiler der Stablängen nach jeder Säge-Runde derselbe wie vor dieser Runde.
Wir können den Algorithmus auch abstrakter aufschreiben. Dann kommen keine Stäbe mehr vor. Die Eingabe sind zwei natürliche positive Zahlen a und b und die Ausgabe ist der größte gemeinsame Teiler, der ggT von a und b. Wir nennen den Algorithmus aus Gründen, die gleich beleuchtet werden, LangsamEuklid.
LangsamEuklid
Schauen wir uns ein konkretes Beispiel an:
Die Eingabe sollen die Zahlen 15 und 9 sein. Im ersten Schritt subtrahieren wir 9 von 15 und erhalten die Zahlen 6 und 9. Im zweiten Schritt erhalten wir die Zahlen 6 und 3. Im dritten Schritt erhalten wir die Zahlen 3 und 3 und der Algorithmus gibt die Zahl 3 aus.
Das nächste Beispiel zeigt, warum wir den Algorithmus LangsamEuklid genannt haben. Betrachte die Eingaben a=1001 und b=2. Die beiden Zahlen während den Iterationen des Algorithmus sind
| 1001 und 2 |
| 999 und 2 |
| 997 und 2 |
| 995 und 2 |
| ... (ziemlich viele Runden) |
| 3 und 2 |
| 1 und 2 |
| 1 und 1 |
Dass es so lange dauert, liegt daran, dass die zweite Zahl sehr klein ist.
Wie oft zieht man die Zahl 2 insgesamt ab? Es gilt 1001 = 2 · 500 +1. Die Zahl 2 wird genau 500 mal von der Zahl 1001 subtrahiert, bis der Wert unter den Wert 2 fällt.
Wie kamen wir auf die Zahl 500? Einfach indem wir 1001 durch 2 geteilt und abgerundet haben. Wir wussten dann, dass 1001 = 500 · 2 + 1 gilt und konnten dann sofort die Zahlen 1001 und 2 durch die Zahlen 1 und 2 ersetzen.
Ein Computer kann sehr schnell eine Division mit Rest ausführen. Diese Operation berechnet aus a und b zwei natürliche Zahlen q und r mit a = q · b + r, wobei r kleiner ist als b. Die Zahl q ist das Ergebnis des Abrundens der Zahl a/b und r ist der Rest der Division von a durch b. In unserem Beispiel ist a = 1001, b=2, q=500 und r=1.
Wenn a und b die Eingabe des Algorithmus LangsamEuklid sind und a größer ist als b, dann wird b von a entweder q-mal subtrahiert (wenn tatsächlich ein Rest bleibt) oder q-1-mal (wenn a durch b teilbar ist und schließlich zwei Stäbe der Länge b entstehen). Wir können den Algorithmus also beschleunigen, indem wir a durch b mit Rest teilen und a sofort durch den Rest r ersetzen. Dabei kann es passieren, dass der Rest r Null ist. Das bedeutet, dass b der gesuchte größte gemeinsame Teiler ist, und der Algorithmus ist fertig.
Dies ist die Idee hinter dem folgenden Algorithmus, den wir jetzt Euklid nennen.
Euklid
Wir können erwarten, dass dieser Algorithmus viel schneller ist als der Algorithmus LangsamEuklid. Warum das so ist, kann man genau begründen. Nehmen wir an, dass a die größere der beiden Zahlen ist. Wie groß ist der Rest r, der bei der Division von a durch b übrig bleibt? Das schauen wir uns an einem Bild an.

Man sieht, dass der Rest immer eine Länge von höchstens a/2 hat. Das liegt daran, dass b+r höchstens a ist und r kleiner als b ist.
Nach einer Runde wird a durch den Rest r ersetzt, welcher höchstens so groß ist wie a/2. In der zweiten Runde wird b durch den Rest der Division von b durch r ersetzt. Diese Zahl ist auch höchstens so groß wie a/2. Also sind nach zwei Runden beide Zahlen höchstens halb so groß wie a, welche die größere Zahl der Eingabe war.
Wenn wir jetzt 2 · k Runden hintereinander betrachten, dann haben beide Zahlen höchstens den Wert a / 2 k. Wenn k > log a, dann hätten beide Zahlen den Wert Null. Das kann aber nicht passieren, da der Algorithmus fertig ist, sobald eine Zahl Null ist. Daher ist die Anzahl der Schleifendurchläufe des Algorithmus höchstens 2 · log a, wobei wir wieder den Logarithmus zur Basis 2 meinen.
Die Anzahl der Ziffern, die wir in unserem Dezimalsystem brauchen um die Zahl a aufzuschreiben ist proportional zu log a. Während der Algorithmus LangsamEuklid eine Laufzeit hat, die proportional zu den Werten von a und b ist, hat der Algorithmus Euklid eine Laufzeit, die proportional zur Anzahl der Ziffern von a und b ist. Das ist ein wesentlicher Unterschied.
Zum Schluss berechnen wir noch von Hand den größten gemeinsamen Teiler von a=1324 und b=145. Die erste Division mit Rest ergibt 1324=9·145+19. Jetzt wird a auf den Wert 145 gesetzt und b auf den Wert 19.
Die zweite Division mit Rest ist 145 = 7· 19 + 12. Die nächste Division mit Rest ergibt 19 = 1· 12 + 7, dann folgen 12 = 7+5, 7=5+2, 5=2· 2 + 1 und 2 = 2 · 1 + 0, woraus wir schließen können, dass der größte gemeinsame Teiler von 1324 und 145 die Zahl 1 ist. Man sagt dann auch, die Zahlen sind teilerfremd.
Der Autor dankt Martin Dietzfelbinger für hilfreiche Kommentare.
Für Inhalte und Verfügbarkeit der externen Links übernehmen wir keine Gewähr. (Haftungsausschluss)
