Autor
Christian Schindelhauer, Universität Freiburg
 Um Hashing zu
erklären, fangen wir mit einen
Häschen an.
Um Hashing zu
erklären, fangen wir mit einen
Häschen an.
Einen Hasen zu finden, ist nicht leicht. Diese scheuen Tiere
können
 sich sehr gut verstecken. Wenn man aufmerksam über ein
verschneites Feld läuft, dann wird man vielleicht die folgenden
Spuren finden:
sich sehr gut verstecken. Wenn man aufmerksam über ein
verschneites Feld läuft, dann wird man vielleicht die folgenden
Spuren finden:
Hier sind zwei Hasen nebeneinander durch den Schnee gehoppelt. Aus
einer Spur kann man allerhand über das Tier erfahren: Wie
groß und wie schwer es ist, ob es in einer Gruppe unterwegs ist
und vieles mehr.
Manchmal findet man in solch einer Spur auch das:

Im Jägerlatein wird das Losung genannt. Es handelt sich um
den Kot des Hasen. Aus der Losung lässt sich ablesen,
was das Tier gefressen hat oder ob es krank ist. Neuerdings kann man
(nach einer Laboranalyse) damit auch ein Tier eindeutig
identifizieren. Das funktioniert bei allen Tierarten durch Analyse der
DNS im Kot (Damit möchte man beispielsweise in Madrid
demnächst der hündischen Umweltverschmutzer habhaft werden).
Message Digest
Was hat das mit dem Algorithmus der Woche zu tun? Nun, eine Losung entsteht, indem der Hase frisst und die Losung ablegt. Also das:

Hierzu wird das Futter zerhackt, vermischt, zerrührt, verdaut,
entwässert und ausgestoßen. Das
Resultat ist ein kleiner Haufen. Das Endprodukt lässt sich
der Eingabe, dem Futter, zuordnen. Hierbei geht natürlich eine
ganze Menge
an Information
verloren; die Zuordnung ist aber immer noch möglich.
Dasselbe lässt sich auch mit digitalen Dokumenten, wie Text-Dokumenten, Musik-Dateien und Film-Dateien durchführen. Für einen Informatiker sind das einfach Folgen von Nullen und Einsen. Hierzu wird das Originaldokument durch eine Folge von Operationen vermengt, vermischt und verdichtet, bis eine Bitfolge fester Länge ausgeschieden wird. Das sieht in etwa so aus:
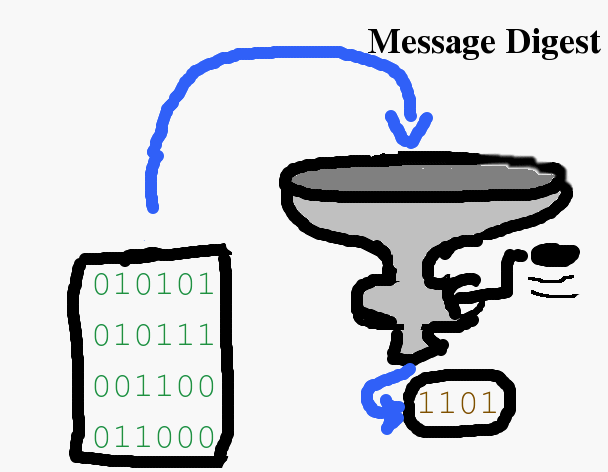
Ein bekannter Algorithmus, der diesen Vorgang durchführt, ist MD-5 (Message Digest 5), was soviel wie Nachrichtenverdauer Version 5 heißt. Er wurde 1991 von Ronald Rivest entwickelt und die genaue Beschreibung kann man bei Wikipedia nachlesen (http://de.wikipedia.org/wiki/MD5). Andere bekannte Algorithmen sind SHA-1, SHA-224, SHA-256, SHA-384 und SHA-512 (http://de.wikipedia.org/wiki/SHA-1). Übersetzt sind das „sichere Hack-Algorithmen“ (Secure Hash-Algorithm). Sie sollen das gleiche leisten wie ein Nachrichtenverdauer.
Sicheres Hashing
Was leisten aber diese Hash-Algorithmen? Zuerst bilden sie Dateien unterschiedlicher Länge auf Bitfolgen fester Länge ab. Als zweites lassen sich aus dem Ergebnis die ursprünglichen Dateien identifizieren, aber nicht unbedingt rekonstruieren. Die ersten beiden Eigenschaften formulieren wir mathematisch:
Mit {0,1}* beschreiben wir die Menge aller Bitfolgen, also {0, 1, 00, 01, 10, 11, 0000, 0001, ...} und auch die leere Bitfolge. Mit {0,1}k beschreiben wir die Menge aller Bitfolgen mit genau k Bits, also: {0..00, 0..01, 0..10 , ... , 1..111}. Eine Hash-Funktion f ist demnach eine Abbildung:
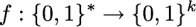
Was bedeutet es nun, dass das Ergebnis einer Hash-Funktion das Original eindeutig identifiziert?
Es heißt, dass f(x) = f(y) genau dann und nur dann richtig
ist, wenn x = y ist.
Das Gegenteil dieser Aussage ist: Es gibt zwei
verschiedene Werte x und y, so dass f(x) = f(y)
ist.
Dieses Zusammentreffen wird Kollision genannt. Wir behaupten also, dass es eine Hash-Funktion für alle Bitfolgen gibt ohne Kollisionen. Mathematisch gesehen ist diese Behauptung absoluter Unfug! Warum?
Stellen wir uns vor, dass jeder Hash-Wert eine Schublade ist, dann gibt es so viele Schubladen wie es Bitfolgen der Länge k gibt, also 2k, nämlich zwei Möglichkeiten für jedes Bit. Wir behaupten also, dass in jede dieser Schubladen f(x) nur eine Originalbitfolge hineingeworfen wird. Davon gibt es aber unendlich viele, also mehr als 2k. Damit müssen in mindestens einer der Schubladen unendlich viele Originalwerte liegen und in dieser Schublade treten unendlich viele Kollisionen auf.
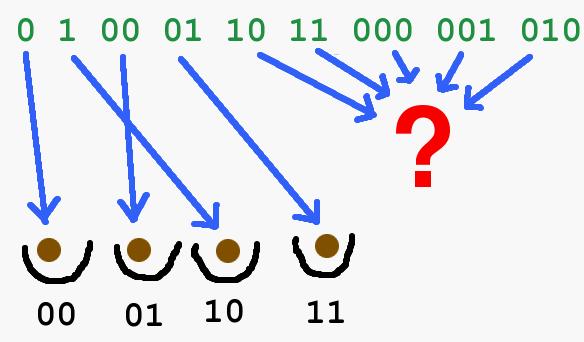
Es gibt aber einen Ausweg! Wir wählen k so groß, dass wir so viele Schubladen haben, dass für jede Datei, die auf Rechnern jemals gespeichert wird, mindestens ein Hash-Wert vorhanden ist. Diese Diskussion kennen wir noch aus der Woche mit der Einweg-Funktion. Also wählen wir zum Beispiel k=512. Dann gibt es 2512 > 10154 Schubladen. Wenn es jetzt gelingt, diese Schubladen so zu füllen, dass keiner (Mensch oder Rechner) eine Kollision konstruieren kann, sind wir aus dem Schneider.

Bis heute ist nicht klar, ob das funktionieren kann. Zwar gibt es mögliche Anwärter wie SHA-512 (mit 512 Bits für den Hash-Wert). Aber das heißt nicht viel. Zum Beispiel galt lange MD-5 als praktisch kollisionsfrei und heute kennt man Methoden zur Konstruktion von beliebig vielen Kollisionen.
Praktisch kollisionsfreie Hash-Funktionen sind in der Informatik sehr nützlich. So kann man damit die Korrektheit von übermittelten Dateien durch einen mit versandten Hash-Wert belegen und dadurch Übertragungsfehler oder Fälschungsversuche entlarven.
Hashing für Wörterbücher
Hash-Funktionen bieten neben der Identifizierung von Dateien auch eine effiziente Möglichkeit zur Speicherung von Daten. Stellen wir uns vor, dass wir einen Speicherbereich S zur Speicherung von insgesamt m Daten zur Verfügung haben. Dieser Speicher ist als Tabelle oder Array organisiert. Man kann also auf den Speicherwert S[1], ..., S[m] jeweils direkt zugreifen. In diesen Speicher wollen wir jetzt Daten ablegen, welche mit einer Bitfolge als Schlüssel identifiziert werden.
Also zum Beispiel:
| Hase |
12 |
| Fuchs |
2 |
| Igel |
4 |
| Bär |
1 |
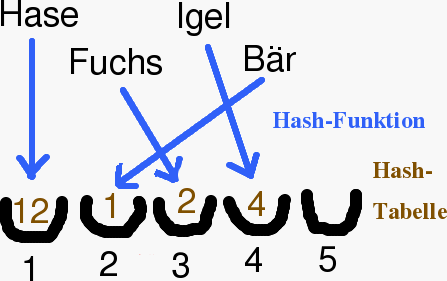
Die Daten sind hier sehr kompakt, während der Suchindex sehr lang ist. Angenommen wir hätten eine Hash-Funktion f, die Zeichenfolgen auf das Intervall {1,2,3,..,m} abbildet, d.h.

Dann könnten wir an die Speicherstelle S[f("hase")] den Wert
12 ablegen, an der Stelle S[f("fuchs")] den Wert 2
ablegen
und so weiter... Diese Operation beschreiben wir mit Put.
 Put (string x, int z)
Put (string x, int z)
begin
S[f(x)] := z
end
Mit Get bekommen wir den Wert
wieder, wobei der Wert 0 anzeigt, dass keine Dateien gespeichert sind.
Get (string x)
begin
return S[f(x)]
end
Leider funktionieren die beiden Funktionen nur, wenn die Hash-Funktion
absolut kollisionsfrei ist. Also wenn z.B. Hase und Igel nicht zusammen
in einem Speicherplatz abgebildet werden. Das kann man für kleine
Werte m nur garantieren, wenn man die Schlüssel vorher kennt (also
Hase, Fuchs, Igel und Bär) und dann eine sogenannte perfekte Hash-Funktion wählt.
Kollisionsbehandlung
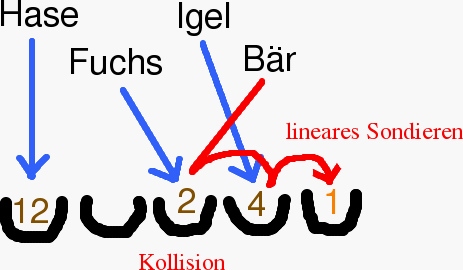 Treten Kollisionen auf, so muss man einen leeren Platz finden.
Dafür gibt es mehrere Methoden. Die einfachste ist das so genannte
lineare Sondieren. Man
speichert hierfür in jedem Tabellenplatz das Datum und den
Schlüssel.
Treten Kollisionen auf, so muss man einen leeren Platz finden.
Dafür gibt es mehrere Methoden. Die einfachste ist das so genannte
lineare Sondieren. Man
speichert hierfür in jedem Tabellenplatz das Datum und den
Schlüssel.
- Speichern von Datum
z unter
Schlüssel x:
Zuerst berechnet man den Hash-Wert von x. Ist der Platz schon mit einem fremden Schlüssel besetzt, so geht man nach rechts weiter, bis man einen leeren Platz findet oder einen Platz mit dem gesuchten Schlüssel. Ist man ganz rechts, so springt man an die erste Stelle und fährt dort fort. Hat man den Tabellenplatz mit dem Schlüssel oder einen leeren Tabellenplatz schlussendlich gefunden, so schreibt man den Schlüssel x und das Datum z dorthin. Ist man einmal erfolglos außen rum gelaufen, so ist der Speicher voll. Das gibt dann eine Fehlermeldung. - Suchen von Datum
unter Schlüssel x:
Wieder wird zuerst der Hash-Wert f(x) von x berechnet. Ist dort ein fremder Schlüssel geht man nach rechts bis man den richtigen Schlüssel oder einen leeren Speicherplatz findet. Stößt man bei dieser Suche auf den rechten Rand, dann sucht man von vorne weiter. Die Suche ist erfolglos, wenn man auf einen leeren Speicherplatz stößt oder einmal rundherum gelaufen ist. Ansonsten hat man den Schlüssel x gefunden und kann das Datum ausgeben.
Mit dieser Kollisionsbehandlung kann man nun immer m Daten speichern, ganz unabhängig von der Güte der Hash-Funktion. Wer diese einmal selbst ausprobieren möchte, kann hierzu als Schlüssel die ganzen Zahlen und als Hash-Funktion die Modulo-m-Funktion benutzen. Das ist der Rest nach der Division durch m. Am Anfang wird das Speichern und Suchen erstaunlich schnell gehen. Aber wenn sich die Tabelle füllt, dann wird der Algorithmus der Woche immer langsamer werden.
Das liegt an der schlechten Kollisionsbehandlung. Denn die lineare Kollisionsbehandlung sucht immer wieder an denselben Stellen. In der Informatik kennt man bessere Lösungen wie z.B. die quadratische Methode oder das doppeltes Hashing. Für diese Woche belassen wir es aber bei einem doppelten Häschen...

- Wikipedia: MD5, SHA-1, Hash-Tabelle
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest - Introduction to Algorithms. 1184 Seiten; The MIT Press 2001, ISBN 0-262-53196-8

