Autor
Markus E. Nebel, TU Kaiserslautern
Viele Objekte, die ein Computer verarbeitet, speichert er intern in Form eines Textes. Das naheliegendste Beispiel ist ein Text selbst, erstellt mit einem Editor oder Textverarbeitungsprogramm, aber auch diese Seite mit dem Algorithmus der Woche wird auf dem Webserver als HTML-Dokument, also als Text mit integrierten Formatierungsbefehlen und Verweisen auf Bilddateien etc., vorgehalten. Wir stellen uns also vor, wir hätten in Google nach etwas gesucht und seien so auf eine Seite mit sehr viel Text gestoßen. Es stellt sich sofort die Frage, wo überall im Text unser Suchwort auftritt. Aus diesem Grund befaßt sich der Algorithmus dieser Woche mit dem sogenannten String Matching Problem, also mit der Suche nach allen Vorkommen eines Wortes w in einem Text t.
Ein Computer speichert Texte zeichenweise ab. Entsprechend ist ein Computer nicht in der Lage, das Wort w mit einem Teil des Textes in nur einem Schritt zu vergleichen, um festzustellen, ob w an der entsprechenden Position im Text vorkommt – auch dieser Vergleich muß Zeichen für Zeichen durchgeführt werden. Wir nehmen also an, daß der Text t aus n, das Wort w aus m Symbolen besteht. Für i eine natürliche Zahl zwischen 1 und n wollen wir mit t[i] das i-te Symbol des Textes bezeichnen; t[1] ist also das erste Symbol des Textes, t[2] sein zweites Symbol usw., t[n] repräsentiert entsprechend das letzte Symbol des Textes. Entsprechend verwenden wir die Notation w[j], um das j-te Symbol des gesuchten Wortes zu bezeichnen. Hier muß j nun eine Zahl zwischen 1 und m sein. Suchen wir beispielsweise im Text „Wir suchen eine Nadel im Heu.“ nach dem Wort „Nadel“, so sehen t und w im Detail aus wie folgt (die Spalte mit der Zahl i enthält dabei das Symbol t[i] bzw. w[i]):

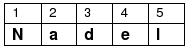
Es sind also n=29 und m=5, und beispielsweise t[1]=W, t[2]=i, w[4]=e usw. Es ist zu beachten, daß auch die Leerzeichen unseres Textes als Symbole gelten und keinesfalls ignoriert werden können. Wir werden nachfolgend immer diesen Text als Beispiel betrachten, dort jedoch nach unterschiedlichen Wörtern w suchen.
Um festzustellen, ob dieser Beispieltext mit w = Nadel beginnt, muß ein Algorithmus den Anfang des Textes t und das Wort w symbolweise vergleichen. Stimmen alle Symbole überein, so wurden wir fündig und das erste Vorkommen von w liegt an erster Position des Textes. Für unser Beispiel ist dies offensichtlich nicht der Fall. Ein Programm muß für diese Feststellung w[1] mit t[1] vergleichen und stellt eine Nichtübereinstimmung fest; t[1] = W < > w[1] = N. Damit kann unser Programm folgern, daß w nicht an erster Position in t vorkommt. Nur wenn alle m Vergleiche der Symbole von w mit den entsprechenden Symbolen von t eine Übereinstimmung ergeben, kommt w an entsprechender Stelle in t vor. In unserem Beispiel genügte ein Vergleich um festzustellen, daß dies nicht der Fall ist, doch das ist natürlich nicht immer so. Suchen wir beispielsweise in unserem Text nach dem Wort Wirt, so führen die drei ersten Vergleiche zu einer Übereinstimmung und erst an vierter Position, beim Vergleich von t[4] mit w[4], würde ein Unterschied zwischen der betrachteten Textstelle und dem Wort entdeckt – das Leerzeichen ist ungleich dem Buchstaben t.
Folgendes kleines Programm führt die eben beschriebenen Vergleiche nacheinander durch. Im Unterschied zu unserer bisherigen Diskussion beginnen wir dabei jedoch mit dem letzten Symbol von w anstatt mit dem ersten. Der Grund hierfür wird uns später klar werden.

Nebenstehende Grafik verdeutlicht das Vorgehen dieses kleinen Programmes am Beispiel des obigen Textes t und w = Kochbuch. Ein grüner Doppelpfeil zwischen zwei Symbolen steht dabei für einen Vergleich zweier identischer Symbole, ein roter Strich verbindet zwei Symbole, für die eine Nichtübereinstimmung entdeckt wurde.
Der Anfang des Textes wird beginnend mit w[8] Symbol für Symbol mit dem Wort w verglichen bis entweder j zu 0 wird (dies ist in unserem Beispiel nicht der Fall) oder die verglichenen Symbole nicht übereinstimmen (geschieht in unserem Beispiel für j=5). Diese beiden Bedingungen werden in der while-Schleife abgefragt. Umgangssprachlich ausgedrückt besagt
while (j > 0) and (w[j] = t[j]) do j := j-1
nämlich, daß j solange um 1 verkleinert werden soll, wie es größer als 0 ist und wie das j-te Symbol des Textes gleich dem j-ten Symbol des Wortes ist. Stimmen die ersten m Symbole des Textes also nicht mit w überein, so ist die zweite Bedingung irgendwann verletzt und j ist dabei noch größer 0. Kommt das Programm dann zur Abfrage if (j = 0) ... wird folgerichtig kein Vorkommen gemeldet (die Ausgabe des Textes "Vorkommen an Position 1" dient uns hier als Platzhalter für eine beliebige Aktion, die wir für ein gefundenes Vorkommen ausführen wollen). Stimmen umgekehrt alle m Symbole von w mit den ersten m Symbolen von t überein, so wird die while-Schleife beendet, da j = 0 gilt. In diesem Fall meldet unser Programm Erfolg.Da die uns gestellte Aufgabe darin besteht, alle Vorkommen von w als Teil von t zu finden, können wir selbstverständlich nicht nur am Anfang von t nach w suchen. Vielmehr kann w ja an jeder beliebigen Stelle von t beginnen, was unser Programm überprüfen muß. Jede beliebige Stelle von t heißt dabei, daß wir ein Vorkommen von w an zweiter, dritter, usw. Position von t vermuten müssen. Für die zweite Position müssen wir dann feststellen, ob w[1] = t[2] und w[2] = t[3] und ... und w[m] = t[m+1] gilt. Entsprechend sind die dritte, vierte, usw. Position zu betrachten. Die letzte mögliche Position ist dabei die (n-m+1)-ste, da dort w[m] = t[n] in Übereinstimmung gebracht wird. Betrachten wir also die Position pos (pos eine Variable), so ist w[1] mit t[pos], w[2] mit t[pos+1], ..., w[m] mit t[pos+m-1] zu vergleichen (unser Algorithmus wird dies wieder in umgekehrter Reihenfolge erledigen). Indem wir in obigem Programm eine zusätzliche Variable pos verwenden, können wir es dahin erweitern, daß es entsprechend unserer Überlegungen w an allen möglichen Positionen des Textes sucht (die von oben übernommenen Programmteile sind blau hervorgehoben).

Die äußere while-Schleife stellt dabei sicher, daß wir tatsächlich alle möglichen Positionen für w als Teil innerhalb t betrachten. Nebenstehende Abbildung verdeutlicht die dafür vorgenommenen Neuerungen an unserem Programm. Für pos=1 werden vier Vergleiche durchgeführt, drei Übereinstimmungen, eine Nichtübereinstimmung. Diese Vergleiche werden auch hier durch die schrittweise Verkleinerung von j realisiert. Durch die anschließende Erhöhung von pos um Eins wird das Wort anschaulich um eine Position nach rechts verschoben. Der dort durchgeführte erste Vergleich ist erfolglos, so daß pos erneut erhöht wird (w anschaulich um eine Position nach rechts verschoben wird) usw.
An dieser Stelle können wir einen ersten Hinweis dazu wagen, warum wir das Wort von rechts nach links mit dem Text vergleichen: Wie wir nachfolgend sehen werden, ist es nicht notwendig, stets alle Positionen (alle möglichen Werte der Variable pos) zu betrachten. Manche können übersprungen werden, ohne eine Vorkommen von w zu verpassen. Ein Vergleich von rechts nach links ermöglich dabei große Sprünge, ohne dafür komplizierte Berechnungen durchführen zu müssen.
Mit diesem Algorithmus haben wir eine erste Lösung für das String-Matching-Problem gefunden. Unser Programm wird stets alle Vorkommen von w innerhalb t finden (wo auch sollte denn noch ein Vorkommen versteckt sein, wenn wir alle möglichen Positionen betrachten?). Zu kritisieren bleibt lediglich der hohe Aufwand, den wir dafür betreiben. Im schlimmsten Fall vergleichen wir nämlich ungefähr Anzahl der Symbole des Textes * Anzahl der Symbole des Wortes oft ein Symbol des Textes mit einem Symbol des Wortes. Ein Beispiel für diese Situation ist der Text t=aaaaaaaaaaaaaa und das Wort w=baaa.
Nun könnte es sein, daß es gar nicht möglich ist, alle Vorkommen von w in t mit weniger Vergleichen zu finden. In diesem Fall bliebe uns nichts anderes übrig, als diesen hohen Aufwand in Kauf zu nehmen. Dies ist aber nicht der Fall, wie nachfolgendes Beispiel verdeutlicht.

Wenn wir in dieser Situation w mit t symbolweise vergleichen, stellen wir fest, daß ein d im Text nicht mit dem g im Wort übereinstimmt. Da das Symbol d in w aber gar nicht vorkommt, kann auch eine oder zwei Positionen weiter rechts kein Vorkommen von w liegen, da jedesmal das d des Textes mit einem Symbol aus w in Übereinstimmung gebracht werden müßte. Wir dürfen w also 3 Positionen nach rechts verschieben (in unserem Programm pos := pos + 3 setzen), ohne ein Vorkommen von w zu verpassen. Dies zeigt, daß unser Algorithmus bisher unnötig viele Positionen betrachtet und dabei unnötig viele Vergleiche durchführt.
Betrachten wir ein weiteres Beispiel (von nun an richten wir den Versatz immer am bisher rechtesten von t betrachteten Symbol aus):

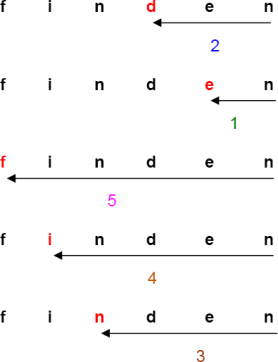
Ist der Vergleich zwischen w und t an der betrachteten Position abgeschlossen (in unserem Beispiel durch den erfolglosen Vergleich zwischen i und n), so können wir w so weit nach rechts schieben, bis das i im Text mit dem rechtesten i in w in Überdeckung gebracht wird. Bei jeder kürzeren Verschiebung von w nach rechts würde irgendwann das i im Text mit einem Symbol von w ungleich i verglichen, was wir schon wissen konnten und somit vermeiden sollten. Verschieben wir beispielsweise w=finden nur um 2 Positionen, steht das d unter dem i; eine programmierte Nichtübereinstimmung. Nur der Versuch, w an der zuvor dargestellten Position zu suchen, macht Sinn, alle kürzeren Verschiebungen von w enden definitiv in einer Nichtübereinstimmung.
Steht in t an der betrachteten Stelle ein Symbol (im nachfolgenden Beispiel das i), das in w gar nicht vorkommt, so können wir entsprechend w um m (hier also um 6) Positionen nach rechts verschieben ohne ein Vorkommen zu verpassen:

Das Wesentliche ist nun, daß die Anzahl der Positionen, um die wir w verschieben können, nur in Kenntnis von w (unabhängig von der gerade betrachteten Position) bestimmt werden kann. Dazu müssen wir uns für ein zu suchendes Wort w nur einmal merken, an der wievielten Position von rechts ein jedes Symbol am weitesten rechts in w vorkommt. Diese Information speichern wir in einer Tabelle D ab, die für jedes mögliche Symbol eine Spalte besitzt. Im folgenden verwenden wir dann D[x], um den Eintrag in der Spalte zum Symbol x zu bezeichnen, für die anderen Symbole entsprechend. Folgende Beispiele verdeutlichen dieses Vorgehen, zur übersichtlicheren Darstellung wurden die Spalten der in w nicht vorhandenen Symbole weggelassen (deren Einträge sind alle gleich der Länge m des Wortes w):
w = finden:
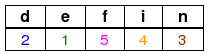
Begründung:
Das letzte n bleibt dabei unberücksichtigt, da es zu einem Eintrag von 0 in der Tabelle führen würde, also zu einem Versatz des Wortes w um keine Position.
w = eine:
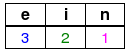
Begründung:
Im Wort eine ist das rechteste e 3, das rechteste i 2 und das rechteste n 1 Symbol vom letzten Symbol entfernt.
Auch hier wird das letzte Symbol (ein e) ignoriert, da seine Berücksichtigung ein Versatz um 0 Positionen bewirken würde,
w = Nadel:
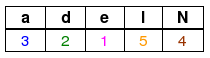
Begründung:
Im Wort Nadel ist das rechteste a 3, das rechteste d 2, das rechteste e 1, das rechteste N 4 Symbole vom letzten Symbol entfernt.
Da das Symbol l nur als letztes Symbol vorkommt, dieses aber ignoriert wird, ist der Eintrag für l derselbe, als gäbe es kein l im Wort, also gleich der Länge 5 des Wortes.
Allgemein können wir die Einträge von D durch folgende Formel beschreiben:

Der erste Fall signalisiert gemäß obiger Beispiele, daß wir w um seine ganze Länge verschieben können, tritt das betrachtete Textsymbol nirgends oder nur an letzter Position in w auf.
Um die Berechnung von D zu programmieren, müssen wir einfach zwei Schleifen wie folgt hintereinander ausführen:
Wir sind nun so weit und können aus unserem naiven Algorithmus den sog. Boyer-Moore-Horspool-Algorithmus machen. Es handelt sich dabei um einen Algorithmus für das String-Matching-Problem, den R. Horspool 1980 als eine Vereinfachung des Algorithmus von Boyer und Moore publizierte. Dazu müssen wir nur
- vor der Suche einmalig D berechnen
- die Zeile pos := pos + 1 durch pos := pos + D[ t[pos + m - 1] ] ersetzen.
Wir erhalten so (die Berechnung von D unberücksichtigt):
Kommt dann der Algorithmus / das Programm an die Stelle, an der w weiter nach rechts verschoben (pos erhöht) wird, wird so sichergestellt, daß an der neuen Position ein Symbol in w mit dem bisherigen t[pos + m - 1] übereinstimmt, ohne dabei ein Vorkommen von w zu verpassen. Auch kann es geschehen, daß w ganz an dem Symbol t[pos + m - 1] vorbeigeschoben wird, falls diese Übereinstimmung unmöglich ist.
Beispiel:

Dabei wissen wir, daß die beiden pink dargestellten Symbole n übereinstimmen, ohne daß wir den entsprechenden Vergleich durchgeführt haben.
Doch was haben wir durch diese Änderung an unserem Programm gewonnen?
Zunächst ist zu sagen, daß wir für die denkbar schlechteste Eingabe gar keine Effizienzsteigerung erreicht haben, da dort D[x] = 1 für alle im Text vorkommenden Symbole x gilt (der Text besteht für einen solchen schlechtesten Fall also aus einer Wiederholung des vorletzten Symbols in w), wir also w weiterhin in Einerschritten nach rechts verschieben. Ein Beispiel für eine solche Eingabe liegt im Text

und dem Wort w = baaaa. In diesem Fall werden für jede Position 5 Vergleiche durchgeführt da die vier a des Wortes stets mit den Symbolen des Textes übereinstimmen und ein fünfter Vergleich erforderlich ist, um festzustellen, daß w an der betrachteten Position nicht vorkommt. Da für dieses w zusätzlich D[a]=1 gilt, werden so insgesamt 25 * 5 = 125 Vergleiche durchgeführt.
Natürlich ist es sehr unwahrscheinlich, daß in der praktischen Anwendung ein solcher Text mit einem solchen Suchwort vorkommt und tatsächlich ist der neue Algorithmus in den allermeisten Fällen der Anwendung wesentlich schneller als unsere naive Lösung. Betrachten wir zum Vergleich noch einmal das Beispiel des Textes

mit dem Suchwort w = Nadel, für das wir ja schon wissen, daß D wie folgt aussieht:

Wie man leicht nachprüfen kann, stellt der naive Algorithmus 29 Vergleiche zwischen Text und Wort an, um das eine Vorkommen von w zu finden. Unser verbesserter Algorithmus ist da wesentlich schneller. Um D zu bestimmen, muß er vor der Suche 5 Symbole betrachten. Für die eigentliche Suche benötigt er dann noch 10 Vergleiche, von denen alleine 5 zur Feststellung des einen Vorkommens von Nadel notwendig sind. Da unser Text 29 Symbole lang ist, können wir folglich einen Text nach allen Vorkommen eines Wortes durchsuchen, ohne alle Symbole des Textes zu betrachten - auf den ersten Blick klingt das verrückt. Schlüssel zu diesem (in den allermeisten Fällen) effizienten Vorgehen war der Vergleich von Text und Wort symbolweise von rechts nach links. Nur so betrachten wir zu anfangs ein Textsymbol (nämlich t[pos + m - 1]), das für spätere Positionen erneut mit w in Übereinstimmung zu bringen ist. Damit ist der Vergleich von rechts nach links Grundlage unserer Verbesserung - eine kleine Modifikation mit großer Wirkung also.

