Autor
Johannes Blömer, Universität Paderborn
In vielen Filmen und Romanen wie Die Piratenbraut, Der Schatz im Silbersee oder Der Schuh des Manitu taucht immer wieder das folgende Motiv auf. Ein Teil einer Schatzkarte wird gefunden. Um den Schatz zu finden, genügt aber dieser Teil der Karte alleine nicht. Vielmehr werden hierzu auch alle anderen Teile der Karte benötigt. Also begibt sich der Finder des Schatzkartenfragments auf die Suche nach den restlichen Teilen. Die Besitzer der anderen Teile sind aber natürlich genauso brennend an den ihnen fehlenden Teilen der Karte interessiert. Und schon kann das Abenteuer beginnen.
Dieses beliebte Film- und Romanmotiv ist ein Beispiel für den aktuellen Algorithmus der Woche: Teilen von Geheimnissen. Dabei interessiert uns die Frage, wie man überhaupt Schatzkarten oder beliebige andere Informationen so in Teile zerlegen kann, dass ohne Kenntnis aller Teile der Schatz nicht gefunden werden kann bzw. die Informationen nicht vollständig rekonstruiert werden können. Wir werden dabei Methoden zum Teilen von Geheimnissen kennen lernen, die deutlich besser sind als das Zerschneiden einer Schatzkarte. Denn es ist nicht wirklich überzeugend, dass man nur mit Hilfe aller Teile einer Karte das Versteck des Schatzes finden kann.
Das allgemeine Problem ist leicht beschrieben. Ein Geheimnis, nennen wir es einfach G, soll in eine bestimmte Anzahl von Teilen zerlegt werden. Die einzelnen Teile werden dann an unterschiedliche Personen verteilt, wobei auf folgende Punkte geachtet wird:
Wenn alle Personen wieder zusammen kommen und ihre Teile des Geheimnisses kombinieren, so können sie das Geheimnis G vollständig rekonstruieren.
Wenn jedoch nur einige, aber nicht alle, der Personen zusammen kommen, so können sie das Geheimnis G nicht vollständig rekonstruieren. Mehr noch, diese Personen können dann keine oder nur sehr wenige Informationen über G aufdecken.
Neben seiner Rolle als Filmmotiv hat das Teilen von Geheimnissen andere, ernstere und realistische Anwendungen. Stellen wir uns etwa vor, dass ein wichtiges Dokument eines Staates oder eines Unternehmens in einem Safe gelagert ist. Man hat sich vorher darauf geeignet, dass dieses Dokument nur dann aus dem Safe genommen und veröffentlicht werden darf, wenn alle Mitglieder einer eigens hierzu eingesetzten Kommission oder eines Gremiums der Veröffentlichung zustimmen. Um dieses zu erreichen, wird der Safe nun mit verschiedenen Schlössern gesichert, genau ein Schloss für jedes Kommissionsmitglied. Jedes Mitglied der Kommission hat nun den Schlüssel zu genau einem Schloss. Soll der Safe geöffnet werden, muss jedes Kommissionosmitglied sein Schloss öffnen und auf diese Weise der Veröffentlichung des Dokuments zustimmen. Mit Hilfe des Teilens von Geheimnissen können wir ebenfalls erreichen, dass das Dokument nur mit Zustimmung aller Mitglieder der Kommission veröffentlicht werden kann. Dazu werden wir den Safe nicht mehr durch mehrere Schlösser sichern und jedem Kommissionsmitglied einen Schlüssel übergeben. Stattdessen sichern wir den Safe durch ein einziges Nummernschloss dessen Geheimnummer zum Beispiel 50 Dezimalstellen besitzt. Jetzt wird die Geheimzahl zur Öffnung des Safes, einfach in so viele Teile aufgeteilt, wie die Kommission Mitglieder hat. Jedes Kommissionsmitglied bekommt dann genau ein Teilgeheimnis. Wenn alle Kommissionsmitglieder sich einig sind, dass der Safe geöffnet werden und das Dokument veröffentlicht werden soll, können sie ihre Teilgeheimnisse nutzen, um die Geheimzahl zu rekonstruieren. Die Teilgeheimnisse kann man sich also wie Schlüssel für verschiedene Schlösser vorstellen, mit denen der Safe gesichert ist. Methoden zum Teilen von Geheimnissen können physische Schlüssel durch Geheimnisse, also Wissen oder Informationen, ersetzen.
Neben dem Verteilen der Geheimzahl eines Safes gibt es noch viele andere Beispiele für Anwendungen des Teilens von Geheimnissen. Es ist sogar so, dass das Teilen von Geheimnissen, wie wir es gleich kennen lernen werden, eines der wichtigen Hilfsmittel der Kryptographie ist, also der Wissenschaft vom Verschlüsseln von Nachrichten oder allgemeiner der Wissenschaft vom Schutz von Informationen vor unbefugtem Zugriff und Veränderung.
Eine einfache Methode zum Teilen von Geheimnissen
Wie aber können wir nun Geheimnisse teilen? Wie können wir Schlösser und die dazugehörigen Schlüssel durch Informationen ersetzen, die jeweils nur ein Mitglied der Kommission kennt? Betrachten wir wieder unser Beispiel des in einem Safe eingeschlossenen Dokuments. Die 50-stellige Geheimzahl des Safes sei etwa
G = 65497 62526 79759 79230 86739 20671 67416 07104 96409 84628
Nehmen wir weiter an, dass dieses Geheimnis unter genau 10 Personen so aufgeteilt werden soll, dass nur alle 10 Personen zusammen die Geheimzahl rekonstruieren können. Wie wäre es mit der Idee, wie in der Abbildung unten jeder Person genau 5 der 50 Stellen zu geben?
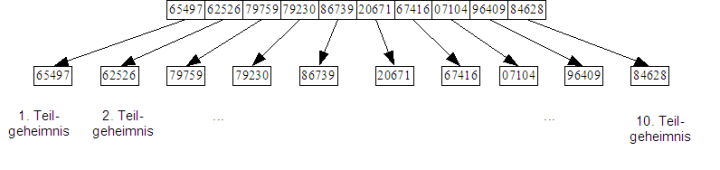
|
Wir sehen schnell, dass das keine gute Idee ist. Denn kommen nur 9 der 10 Personen zusammen, so sollten diese 9 Personen ja eigentlich nichts oder zumindest nicht sehr viel über die Geheimzahl erfahren. Nun kennen sie aber bereits 45 der 50 Stellen der Geheimzahl und damit 9/10 des Geheimnisses. Die letzten 5 Stellen, die ihnen noch fehlen, können sie durch Ausprobieren herausfinden. Die Anzahl der Möglichkeiten für die fehlenden 5 Stellen ist 105=100000. Es mag recht lange dauern, diese Stellen durch Ausprobieren zu bestimmen. Unmöglich ist es aber sicherlich nicht. Damit können dann 9 Personen ohne die Zustimmung der 10. Person den Safe öffnen und das Dokument veröffentlichen.
Der nächste Versuch bringt uns unserem Ziel schon etwas näher. Um das Geheimnis G, die Geheimzahl mit 50 Dezimalstellen auf die 10 Mitglieder der Kommission aufzuteilen, wählen wir 10 zufällige Zahlen, die alle größer als Null sind und deren Summe genau G ergibt. Die Teilgeheimnisse sind dann die 10 zufällig gewählten Zahlen. Betrachten wir ein kleines Beispiel, in dem G eine ganze Zahl ist und die Teilgeheimnisse Zahlen zwischen 1 und 50 sind. Außerdem soll das Geheimnis nur auf 4 Mitglieder aufgeteilt werden. Sei jetzt G=129. Dann können die Teilgeheimnisse zum Beispiel 17, 47, 31 und 34 sein, denn 17+47+31+34=129. In diesem Verfahren ist klar, dass mit Kenntnis aller Teilgeheimnisse das Geheimnis G bestimmt werden kann. Aber es gibt ein etwas größeres Problem: Wie können die Teilgeheimnisse so gewählt werden, dass nur ein Teil der Kommissionsmitglieder nichts oder wenig über das Geheimnis G erfährt? Leider ist dieses Problem in diesem Verfahren auch nicht so ohne weiteres zu lösen. So erfahren in unserem Beispiel die ersten drei Teilnehmer aus ihren Geheimnissen, dass das Geheimnis G zwischen 17+47+31=95 und 200 liegt. Sie haben also die Möglichkeiten für das Geheimnis fast halbiert. Mit Hilfe eines kleinen Tricks können wir jedoch das Verfahren so ändern, dass nur alle Kommissionsmitglieder zusammen das Geheimnis rekonstruieren können, während Nichts über das Geheimnis verraten wird, wenn sich nicht alle Kommissionsmitglieder an der Rekonstruktion beteiligen. Der Trick besteht darin, die Division mit Rest zu verwenden.
Das Verfahren zum Teilen von Geheimnissen sieht dann folgendermaßen aus. Nehmen wir an, das zu teilenden Geheimnis G ist eine Zahl zwischen 0 und einer großen Zahl N. In unserem Beispiel oben ist N=1050. Dieses Geheimnis soll weiterhin auf 10 Personen aufgeteilt werden, wobei das Verfahren aber für jede beliebige Anzahl von Personen funktioniert. Wir gehen in zwei Schritten vor:
Zunächst wählen wir 9 zufällige Zahlen zwischen 0 und N. Wir nennen diese Zahlen t1, t2, ..., t9. Diese Zahlen sind die Teilgeheimnisse der ersten 9 Personen.
Um das 10. Teilgeheimnis t10 zu bestimmen, bilden wir zunächst t1+...+ t9 und dividieren diese Summe durch N. Von dieser Division nehmen wir den Rest R und bilden die Differenz G-R. Falls G-R positiv ist, so ist dies unser gesuchtes t10. Falls G-R negativ ist, so ist G-R+N unser t10. Durch diese Vorschrift gilt, dass t1+t2+...+t10 bei Division durch N den Rest G ergibt.
Betrachten wir ein kleines Beispiel, in dem wir die Werte der Teilgeheimnisse leicht per Hand ausrechnen können. Wir wählen N=53 und m=4. Das zu teilende Geheimnis sei 23.
Wir wählen nun zunächst die ersten drei Teile der Geheimnisses. Seien diese 17, 47 und 31.
Um das vierte Teilgeheimnis zu bestimmen, berechnen wir zunächst die Summe der ersten drei Teilgeheimnisse, also 17+47+31=95. Wir addieren nun zu 95 noch 34 hinzu und erhalten 129. Bei Division mit Rest von 129 durch 53 erhalten wir 23, das Geheimnis. Als viertes Teilgeheimnis müssen wir daher 34 wählen.
Dargestellt haben wir unser Vorgehen in der folgenden Skizze.
| ( | 17 | + | 47 | + | 31 | + | 34 | ) | : | 53 | = | 2 | Rest | 23 |
| Teilgeheimnisse: | ||||
| Geheimnis: |
Liefert dieses Verfahren uns auch die gewünschten Eigenschaften? Betrachten wir unser Beispiel. Kommen alle vier Besitzer der Teilgeheimnisse zusammen, so können sie die Summe ihrer Teile berechnen und dann den Rest bei Division mit N=53 bestimmen. Sie erhalten zunächst als Summe den Wert 129 und dann als Rest bei Division mit 53 den Wert 23, also genau das Geheimnis. Dasselbe Verfahren funktioniert auch im allgemeinen Fall. Denn das Geheimnis selber ist immer der Rest bei Division durch N der Summe der Teilgeheimnisse. Damit können alle Personen zusammen das Geheimnis rekonstruieren.
Wie sieht es nun aus, wenn nicht alle Personen zusammen kommen? Zunächst einmal sieht es so aus, als ob wir den letzten Teilnehmer etwas anders behandelt haben als die Übrigen, denn sein Teilgeheimnis hängt von den anderen Teilgeheimnissen ab, während dieses bei den ersten Teilgeheimnissen nicht der Fall zu sein scheint. Bei genauerem Hinsehen stellt man aber fest, dass dieser Eindruck täuscht. Gehen wir wieder zu unserem Beispiel und nehmen wir das erste Teilgeheimnis 17. Betrachten wir nun die Summe der übrigen Teilgeheimnisse, so erhalten wir 47+31+34=112. Bestimmen wir nun die eindeutige Zahl x, so dass 112+x bei Division mit Rest durch 53 den Wert 23 liefert, so erhalten wir x=17. Wir sehen, dass das erste Teilgeheimnis von den übrigen drei Teilgeheimnissen auf die gleiche Art abhängt wie das letzte Teilgeheimnis von den ersten drei Teilgeheimnissen.
Was passiert also, wenn nicht alle Personen zusammen kommen? Kann auf einige Teilgeheimnisse bei der Rekonstruktion des Geheimnisses verzichtet werden? Betrachten wir wieder unser Beispiel. Wir nehmen an, die letzten drei Teilnehmer kommen zusammen, um etwas über das Geheimnis zu erfahren. Sie kennen damit die Teilgeheimnisse 47, 31 und 34. Sie kennen auch die Zahl 53. Sie wissen jedoch nicht das Teilgeheimnis des ersten Teilnehmers. Das Geheimnis selber ist ja der Rest bei Division durch 53 der Summe der Teilgeheimnisse. Die Summe der Teilgeheimnisse der letztem drei Teilnehmer ist 112. Bei Division mit Rest durch 53 liefert 112 den Wert 6. Hätte nun der erste Teilnehmer statt der 17 das Teilgeheimnis 0 erhalten, so wäre das Geheimnis 6 und nicht 23 gewesen. Wäre das erste Teilgeheimnis 1 gewesen, so wäre das Geheimnis 7 gewesen. Und so geht es weiter, bis bei den Teilgeheimnissen 51 und 52 für den ersten Teilnehmer das Geheimnis 4 beziehungsweise 5 gewesen wäre. Genauer: Es gibt zu jeder Zahl g zwischen 0 und 53 eine andere Zahl t, so dass die Summe von 112 und t bei Division mit Rest durch 53 die Zahl g ergibt. Das aber heißt, dass bei Teilgeheimnis t für den ersten Teilnehmer und den Teilgeheimnissen 47, 31 und 34 für die anderen Personen das Geheimnis g und nicht G=23 gewesen wäre. Die letzten drei Teilnehmer können also nur mit Kenntnis ihrer drei Teilgeheimnisse keinen der möglichen Werte für das Geheimnis insgesamt ausschließen. Dieses heißt dann aber auch, dass die letzten drei Teilnehmer nur mit Kenntnis ihrer Teilgeheimnisse nichts über das Geheimnis erfahren. Dies gilt auch ganz allgemein.
Allerdings muss man darauf achten, die Zahlen nicht zu klein zu wählen. In unserem Beispiel mit N=53 ist es sicherlich kein Problem alle Möglichkeiten für ein fehlendes Teilgeheimnis auszuprobieren, schließlich gibt es ja nur 53 mögliche Werte für jedes Teilgeheimnis. Einfacher noch gibt es ja insgesamt nur 53 Möglichkeiten für das Geheimnis selbst, die man leicht alle ausprobieren kann. In Anwendungen des Geheimnisteilens wird daher auch mit deutlich größeren Werten als 53 für N gearbeitet. Da wird dann N vielleicht als 1050 gesetzt. Dann gibt es für jedes Teilgeheimnis auch 1050 Möglichkeiten. In diesem Fall ist es völlig utopisch ein fehlendes Teilgeheimnis durch Ausprobieren zu bestimmen.
Allgemeines Geheimnisteilen
Als nächstes wollen wir sehen, ob man Geheimnisse auch so teilen kann, dass nicht unbedingt alle Personen zusammen kommen müssen, um das Geheimnis aufzudecken. Vielmehr soll eine genügend große Anzahl von Teilnehmern bereits ausreichen, um das Geheimnis aufzudecken. Mit anderen Worten, wenn genügend viele Teilnehmer sich einig sind, so sollen sie das Geheimnis rekonstruieren können.
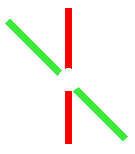
Zum Aufwärmen betrachten wir ein Beispiel, bei dem ein Geheimnis so auf drei Personen verteilt werden soll, dass jeweils zwei von ihnen das Geheimnis aufdecken können. Einer alleine soll jedoch nichts oder möglichst wenig aus seinem Teilgeheimnis auf das Geheimnis schließen können. Unsere Idee von oben, das Geheimnis als Summe von Teilgeheimnissen darzustellen, führt nun leider nicht weiter. Wir brauchen eine neue Idee. Etwas Geometrie hilft uns weiter. Das Geheimnis sei nun ein Punkt P in der Ebene. Wir können uns dabei vorstellen, dass die Koordinaten des Punktes P zusammen die Geheimzahl eines Safes bilden. Weiter wählen wir drei Geraden, die sich alle in diesem Punkt P schneiden. Die drei Geraden sind nun die Teilgeheimnisse. Wir haben dieses in dem folgenden Bild dargestellt.

|
|
Bild 1:
Drei Geraden, die sich in einem Punkt schneiden. Der Schnittpunkt ist das Geheimnis. |
Kommen nun zwei der drei Teilnehmer zusammen, so können sie den Schnittpunkt ihrer beiden Geraden berechnen. Dieses liefert ihnen genau das Geheimnis P. Dieses sieht man auch auf den folgenden drei Bildern.

|
|

|
| Bild 2.1: Mit Hilfe der grünen und blauen Geraden kann das Geheimnis bestimmt werden. | Bild 2.2: Mit Hilfe der grünen und roten Geraden kann das Geheimnis bestimmt werden. | Bild 2.3: Auch mit Hilfe der roten und blauen Geraden kann das Geheimnis bestimmt werden. |
Wie viel erfährt nun ein einziger Teilnehmer durch sein Teilgeheimnis über das Geheimnis P? Nun, er lernt schon etwas dazu. Denn zunächst einmal ist ja das Geheimnis ein beliebiger Punkt in der Ebene. Nachdem ein Teilnehmer sein Teilgeheimnis erfahren hat, weiß er jedoch, dass das Geheimnis P auf der Geraden liegt, die sein Teilgeheimnis ist. Er hat also schon etwas dazu gelernt. Aber er kennt nicht das Geheimnis selber.
Man kann dieses Verfahren leicht verallgemeinern, so dass je zwei von m beliebigen Teilnehmern aus ihren Teilgeheimnissen ein Geheimnis rekonstruieren können. Hierzu ist das Geheimnis wieder ein Punkt P in der Ebene. Die m Teilgeheimnisse sind dann m Geraden, die sich alle im Punkt P schneiden.
Wie sieht es aus, wenn jeweils nur drei der Teilnehmer das Geheimnis rekonstruieren können sollen? Nun müssen wir die Ebene verlassen und in den (3-dimensionalen) Raum gehen. Wieder wählt man als Geheimnis einen Punkt, diesmal allerdings im Raum. Als Teilgeheimnisse wählen wir nun Ebenen und zwar so, dass sich je drei dieser Ebenen genau in dem Punkt P schneiden. Wir haben dieses in den folgenden Bildern für 4 Teilnehmer dargestellt.
|

|
|
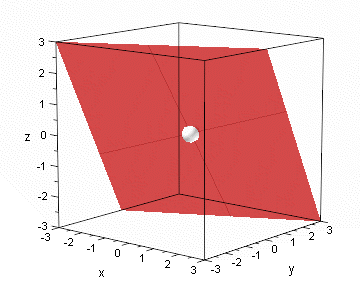
Bild 3.1:
Das Geheimnis P ist der weiße Punkt in der Mitte. Er liegt in der roten Ebene. |
Bild 3.2: Das Geheimnis liegt auch im Schnitt der grünen und roten Ebene. Damit liegt er auch auf der Schnittgerade der grünen und roten Ebenen. |
|
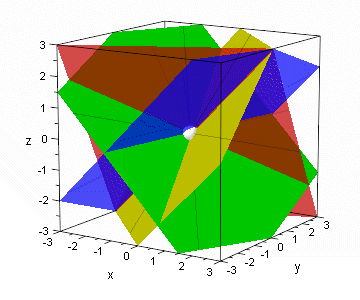
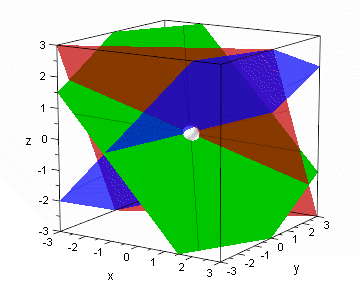
|
| Bild 3.3: Das Geheimnis liegt im Schnitt der grünen, roten und blauen Ebene. Diese drei Ebenen bestimmen das Geheimnis eindeutig. | Bild 3.4: Das Geheimnis liegt im Schnitt der vier Ebenen (rot, gelb, grün, blau). Je drei dieser Ebenen genügen, um das Geheimnis zu bestimmen. |
Drei der Teilnehmer können also immer das Geheimnis bestimmen, indem sie den gemeinsamen Schnittpunkt ihrer Ebenen bilden. Man kann dies in Bild 3.3 oben gut erkennen. Allerdings lernen auch weniger als drei Teilnehmer immer etwas über das Geheimnis. Kommen z.B. nur zwei der Teilnehmer zusammen, so schneiden sich ihre Ebenen in einer Geraden. Man kann dieses an der roten und grünen Ebene in Bild 3.2 erkennen. Kombinieren also die Besitzer der roten und grünen Ebene ihre Teilgeheimnisse, so wissen sie, dass das Geheimnis P auf der Schnittgeraden der roten und grünen Ebene liegt. Allerdings haben sie keine Ahnung, welcher Punkt auf der Geraden das Geheimnis ist.
Ausblicke
Ganz allgemein können wir uns nun fragen, ob ein Geheimnis G so auf m Personen aufgeteilt werden kann, dass je t oder mehr das Geheimnis rekonstruieren können, weniger als t Teilnehmer jedoch wenig oder gar nichts über das Geheimnis lernen. Die Antwort ist, dass dieses möglich ist. Eine Realisierung besteht in einer Verallgemeinerung unserer geometrischen Konstruktion. Man muss dann bei t aus m Teilnehmern in den so genannten t-dimensionalen Raum gehen.
Es gibt auch Konstruktionen bei denen weniger als t Teilnehmer absolut nichts über das Geheimnis erfahren. Diese beruhen allerdings nicht auf dem Schnitt von Ebenen sondern auf so genannten Polynomen.
Wer teilt eigentlich das Geheimnis auf? Diese Frage haben wir bislang völlig ausgeklammert. Sie ist aber natürlich wichtig, denn diejenige Person, die das Geheimnis aufteilt, wird dieses auch kennen. Wenn man das Teilen von Geheimnissen in der Kryptographie anwenden will, bleibt häufig nichts anderes übrig als anzunehmen, dass es eine besonders vertrauenswürdige Person gibt, die man mit dem Aufteilen des Geheimnisses beauftragen kann, ohne dass diese Person versuchen wird, daraus einen Nutzen zu ziehen. Stellt euch hierzu einfach einmal Bill Gates vor, der mit dem Teilen einer Schatzkarte für einen Schatz von 100.000€ beauftragt wird. Bill Gates ist so unvorstellbar reich, dass ihm ein Schatz dieser Größe vermutlich vollkommen uninteressant erscheint.
Was heißt es eigentlich, Informationen zu gewinnen? Was ist Information eigentlich? Irgendwie wissen wir das sicherlich alle. Aber wenn man Informationen mathematisch betrachten will, muss man schon genauer sein. Beim Teilen von Geheimnissen zum Beispiel, wie wir es vorgestellt haben, will und muss man präzise sagen, was es eigentlich heißt, nichts erfahren zu haben. Aber wenn man einmal verstanden hat, warum unsere oben vorgestellten Methoden zum Teilen von Geheimnissen funktionieren, ist es nicht mehr schwer, Begriffe wie Information oder Informationsgewinn mathematisch präzise zu definieren. So liefern Teilgeheimnisse eben keinerlei zusätzliche Informationen über das Geheimnis, wenn man die Möglichkeiten für die Werte des Geheimnisses überhaupt nicht durch die Kenntnis der Teilgeheimnisse einschränken kann. Es war der bedeutende Mathematiker Claude Shannon, der schon um 1948 auf diesem Wege die so genannte Informationstheorie begründete.
Wir können aber auch noch etwas weiter gehen. Was nützt es uns, wenn wir Informationen zwar prinzipiell gewinnen können, aber dieses nur mit extrem hohem Zeitaufwand möglich ist. Das Teilen von Geheimnissen bietet hier wieder ein gutes Beispiel. Egal wie wir die 50-stellige Geheimzahl eines Safes auf die 10 Mitglieder einer Kommission verteilen, prinzipiell ist es natürlich möglich, die Geheimzahl zu bestimmen. Es gibt 1050 Möglichkeiten für die Geheimzahl. Diese Möglichkeiten können prinzipiell natürlich alle ausprobiert werden, um die Geheimzahl zu bestimmen. Aber die Betonung liegt hierbei auf prinzipiell. Denn 1050 ist eine so unvorstellbare große Zahl, dass niemand, nicht einmal mit Hilfe eines Computers, alle 1050 Möglichkeiten wirklich schnell ausprobieren kann. Wir können also sagen, dass ein Geheimnis bereits dann nicht aufgedeckt werden kann, wenn das Zeitaufwand, der für das Aufdecken benötigt wird, zu groß ist als dass man das Geheimnis praktisch wirklich berechnen kann. Diese Überlegungen führen über die oben erwähnte Informationstheorie hinaus. Sie führen zu der Frage, wie viele Ressourcen eigentlich benötigt werden, um etwas zu berechnen oder Informationen zu gewinnen und damit zu Kernfragen und Problemen der Informatik.
- Einträge bei Wikipedia zu den Themen

