Autor
Dirk Bongartz, RWTH Aachen
Walter Unger, RWTH Aachen

Wenn man das Verfahren kennt, dann kann man eine abgefangene "Geheimnachricht" sicherlich leicht entschlüsseln. Was steckt zum Beispiel hinter der folgenden Nachricht?
Wenn man es etwas allgemeiner haben möchte, kann man sich natürlich auch eine Zahl k (<26) wählen und dann die Buchstaben der Nachricht, die man gerne verschlüsseln möchte (nennt man auch Klartext), jeweils um k Positionen im Alphabet nach rechts verschieben. Auf diese Weise erhalten wir dann wieder eine verschlüsselte Nachricht (diese wird als Krypttext oder Chiffre bezeichnet). Das Verschlüsselungsverfahren ist hier das Verschieben der Buchstaben im Alphabet und k wird als (geheimer) Schlüssel bezeichnet. Wenn man nun wieder entschlüsseln möchte, dann muss man nur die Buchstaben im Krypttext jeweils um k Positionen nach links im Alphabet verschieben.
Wenn bei einem solchen Verfahren jemand den Schlüssel kennt, dann kann er sowohl verschlüsseln als auch entschlüsseln. Deshalb nennt man diese Verfahren auch symmetrische Verfahren. Das One-Time-Pad aus dem 26. Algorithmus der Woche ist übrigens auch ein symmetrisches Verfahren. Das heißt, jeder der eine Nachricht verschlüsseln kann, kann andere Nachrichten, die mit dem gleichen Verfahren und mit dem gleichen Schlüssel verschlüsselt wurden, auch entschlüsseln.
Wenn man diese Überschrift liest, dann erscheint sie erst mal unsinnig. Das kann doch gar nicht klappen — das haben wir doch oben beim Caesar-Verfahren gesehen, oder?! Denn wie sollte ein Verschlüsselungsverfahren funktionieren, bei dem der Schlüssel öffentlich ist? Aber das erscheint nur im ersten Augenblick so. Es bräuchte ja nur die Verschlüsselung mit einem öffentlichen Schlüssel durchgeführt zu werden. Der Schlüssel zur Entschlüsselung könnte weiterhin geheim bleiben. Wäre es also nicht super, wenn jeder euch eine Geheimnachricht schicken könnte, aber nur ihr selbst könntet sie entschlüsseln?
Eigentlich ist das doch gar nicht so schwer. Stellt euch vor, ihr würdet Tausende von Vorhängeschlössern kaufen, die aber alle mit dem gleichen Schlüssel geöffnet werden können (ok, so etwas gibt es normalerweise nicht im Laden zu kaufen — da gibt es vermutlich eher ein Schloss mit mehreren Schlüsseln — aber wir können ja mal so tun als ob). Dann verteilt ihr die geöffneten Schlösser in eurer Schule, z.B. im Sekretariat, in der Bibliothek, und so weiter. Zum Schließen der Schlösser braucht man keinen Schlüssel — sie schnappen einfach zu! Den Schlüssel behaltet ihr.
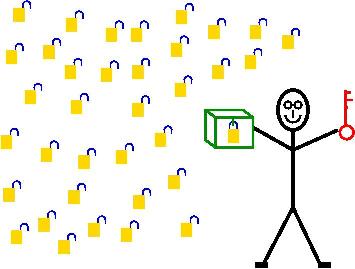
Dann kann jeder, der euch eine geheime Nachricht schicken will, eine Kiste nehmen, die geheime Nachricht dort hineinlegen, die Kiste mit einem eurer Vorhängeschlösser verschließen und sie ruhig dem größten Klatschmaul der ganzen Schule mitgeben, das sie euch überbringt. Keiner außer euch wird die geheime Botschaft lesen können.
Nun ja, es funktioniert also. Aber wir haben schon einen ziemlichen Aufwand getrieben — so viele Schlösser herzustellen und zu verteilen, dürfte wohl ziemlich teuer werden... Kann man das Problem denn nicht ohne Kisten und Vorhängeschlösser lösen? Wir hatten da doch mal was — es gab da diese Einwegfunktionen im 17. Algorithmus der Woche. Was war das noch einmal? Ach ja, das waren Funktionen, bei denen die Berechnung des Funktionswertes "einfach" war, die andere Richtung, also die Umkehrfunktion, aber schwer zu berechnen war (wenn wir das mal so salopp zusammenfassen). Bei uns bräuchten wir also etwas, wo das Verschlüsseln einfach ist (damit alle eine Nachricht für uns verschlüsseln können) und nur das Entschlüsseln schwer ist. Allerdings sollten wir selbst natürlich entschlüsseln können — also benötigen wir noch so etwas wie eine Hintertür, damit es funktioniert.
Das funktioniert auch, wenn man zum Beispiel das inverse Telefonbuch aus dem 17. Algorithmus
der Woche verwendet. Wir benutzen hier aber eine andere Idee.
Solche sogenannten Public-Key-Verfahren werden auch bei der Verschlüsselung von Nachrichten am Computer verwendet. Diese benutzen aber eine relativ komplexe Mathematik, die wir hier gar nicht beschreiben möchten. Wir können das Verfahren aber auch mit ganz einfach mit eingeschränkter Mathematik illustrieren.
Diese eingeschränkte Mathematik kennt nur Addition, Subtraktion und Multiplikation auf ganzen Zahlen. In dieser eingeschränkten Mathematik gibt es insbesondere niemanden, der dividieren kann. Versetzt euch einfach in die Zeit zurück, wo ihr gerade die Multiplikation in der Schule gelernt hattet und noch nicht wusstet, wie dividiert wird. Und mit dieser eingeschränkten Mathematik beschreiben wir nun, wie Simone eine Nachricht an Eike schickt. Diese Nachricht wird aus einer Zahl bestehen.
Das Verfahren wird in drei Schritten beschrieben. Das Erzeugen der beiden Schlüssel, das Verschlüsseln und das Entschlüsseln.
- Aufbau der Schlüssel
Zuerst brauchen wir einen Schlüssel. Um genau zu sein, brauchen wir zwei Schlüssel, einen geheimen und einen öffentlichen. Die Nachricht soll von Simone an Eike geschickt werden. Daher braucht Eike den geheimen Schlüssel, um die Nachricht zu entschlüsseln. Dazu denkt sich Eike zwei Zahlen aus und multipliziert diese. Die erste Zahl nennen wir privater Schlüssel, die zweite ist dann zusammen mit dem Produkt der öffentliche Schlüssel. Damit besteht der private Schlüssel aus einer Zahl und der öffentliche Schlüssel aus zwei Zahlen (nämlich dem öffentlichen Faktor und dem öffentlichen Produkt).

p privater Schlüssel 11 öffentlicher Faktor 143 öffentliches Produkt Da ihr ja dividieren könnt, ist es für euch nun einfach den privaten Schlüssel — also das p — zu bestimmen. Aber wenn man von unserer eingeschränkten Mathematik ausgeht, so ist dieser private Schlüssel weiterhin geheim.
An das schwarze Brett der Schule hängt Eike nun einen Zettel. Jeder kann ihn lesen, da aber keiner dividieren kann, bleibt trotzdem der private Schlüssel p von Eike geheim.
- Das Verschlüsseln
Simone liest diesen Zettel und sie will Eike eine Nachricht schicken. Das ist der Termin der nächsten Fete, der 5. Dezember 2006. Dabei besteht die Nachricht nur aus der 5, denn Simone macht immer im Dezember eine Fete und das wissen schon alle.
Simone beginnt nun mit der Verschlüsselung. Sie kennt die öffentlichen Zahlen 11 und 143 von Eike und die zu verschlüsselnde Nachricht 5.
Zusätzlich zur zu verschlüsselnden Nachricht denkt sich Simone noch eine geheime Zahl aus, diese Zahl nennen wir Sendegeheimnis. Damit rechnet sie nun die verschlüsselten Daten aus. Die verschlüsselten Daten bestehen aus zwei Zahlen, der verschlüsselten Nachricht und einer Entschlüsselungshilfe.
Simone bestimmt das Produkt aus dem Sendegeheimnis und dem öffentlichen Produkt von Eike. Um ihre Nachricht zu verschlüsseln addiert Simone dieses Produkt nun einfach zur Nachricht hinzu. Wenn Simone als Sendegeheimnis die Zahl 3 gewählt hat, dann ergibt sich als verschlüsselte Nachricht: 5 + 3 · 143 = 434. Diese 434 würde veröffentlicht werden, aber die 3 muss geheim bleiben. Ansonsten könnte jeder ausrechnen: 434-3 · 143 = 5.
Da nun die 3 als Sendegeheimnis ja schon bekannt ist, wählt Simone ein anderes Sendegeheimnis, nennen wir es einfach s. Simone rechnet die verschlüsselte Nachricht aus:
5 + s · 143 = 1292 Die 1292 wird veröffentlicht werden, aber das Sendegeheimnis s wird geheim bleiben.
Wenn nur Simone das Sendegeheimnis kennt, ist es keinem möglich, aus der verschlüsselten Nachricht die Nachricht zu bestimmen. Wie kann nun aber Eike entschlüsseln? Denn auch Eike kennt das Sendegeheimnis nicht. Damit Eike, und auch nur Eike, entschlüsseln kann, berechnet Simone als Entschlüsselungshilfe noch das Produkt aus Sendegeheimnis und öffentlichem Faktor.
Simone berechnet 11 · s = 99. Diese Zahl wird auch veröffentlicht. Simone geht zum schwarzen Brett der Schule und hängt da folgenden Zettel aus.

Damit sind die folgenden Zahlen allen bekannt, denn jeder konnte die beiden Zettel am schwarzen Brett lesen.
11 öffentlicher Faktor von Eike 143 öffentliches Produkt von Eike 1292 verschlüsselte Nachricht (= Nachricht + Sendegeheimnis · 143) 99 Entschlüsselungshilfe (= Sendegeheimnis · 11) Selbst wenn jeder weiß, wie Simone gerechnet hat, müsste man wieder dividieren können, um aus den Zahlen das Sendegeheimnis s oder den privaten Schlüssel p zu bestimmen. Und ohne das Sendegeheimnis kann auch niemand Simones geheime Nachricht herausbekommen.
- Das Entschlüsseln
Nun will Eike die Nachricht von Simone entschlüsseln. Eike kann aber wie alle anderen nicht dividieren. Eike kennt aber ihren privaten Schlüssel p. Schauen wir uns nun die verschlüsselte Nachricht genauer an.
1292 Nachricht + Sendegeheimnis · 143 = Nachricht + Sendegeheimnis · öffentliches Produkt = Nachricht + Sendegeheimnis · öffentlicher Faktor · privater Schlüssel = Nachricht + Entschlüsselungshilfe · privater Schlüssel Damit kann nun Eike durch folgende Rechnung an die Nachricht gelangen.

1292 - 99 · (privater Schlüssel p) = 5 Wie man sieht, hat Eike keine Division gebraucht.
- Der Lauscher
Wenn man Filme mit Spionen und Agenten sieht, dann sieht man oft wie Telefonate und andere Gespräche belauscht werden. Um so etwas zu verhindern, werden in den Filmen sichere Leitungen benutzt. Aber dann muss man sich darauf verlassen, dass genau diese Leitung auch wirklich sicher ist.
Hier haben wir keine sichere Leitung gebraucht. Als Leitung wurde das schwarze Brett verwendet. Wir alle waren die Lauscher. Wir haben alle Nachrichten zwischen Eike und Simone mitgelesen. Aber trotzdem war es uns — in der eingeschränkten Mathematik — nicht möglich die geheime Nachricht zu entschlüsseln. Eike und Simone mussten nur jeweils eine Zahl geheim halten. Auch brauchten sie kein gemeinsames Geheimnis. Sie mussten sich nie treffen, um einen Schlüssel, wie z.B. beim One-Time-Pad, auszutauschen.
Wenn also in einem Film eine sichere Leitung benutzt wird, dann stelle man sich wohl besser eine Leitungsverbindung vor, die mit unserem Trick und weiterer Technik verschlüsselt worden ist.
- Ohne eingeschränkte Mathematik
Solange keiner dividieren kann, ist das Verfahren also sicher. Aber spätestens mit dem Schulabschluss weiß man, dass es Menschen und Programme gibt, die dividieren können
 .
Wer auch noch gut aufgepasst hat, sieht wie man mit Hilfe eines der bereits
vorgestellten Verfahren das Ergebnis der Division auch recht schnell bestimmen kann.
Falls man aber nur mit Resten rechnen würde, dann schlägt dieses Verfahren fehl.
.
Wer auch noch gut aufgepasst hat, sieht wie man mit Hilfe eines der bereits
vorgestellten Verfahren das Ergebnis der Division auch recht schnell bestimmen kann.
Falls man aber nur mit Resten rechnen würde, dann schlägt dieses Verfahren fehl.
Tja, damit kann das obige Verfahren nur in unserer speziellen, eingeschränkten Mathematik funktionieren.
Es gibt aber weitere Operationen in der Mathematik. Und diese benutzt man statt Addition, Subtraktion und Multiplikation. Zum Beispiel wird folgendes gemacht.
- Statt der Addition wird die Modulare Multiplikation benutzt.
(Die Modulare Multiplikation ist eine Multiplikation, welche auf Restklassen arbeitet. Betrachte dazu auch den 28. Algorithmus der Woche, in dem modulare Addition zum Teilen von Geheimnissen verwendet wird.) - Statt der Subtraktion wird die Modulare Division benutzt.
- Statt der Multiplikation wird die Modulare Exponentation benutzt.
- Statt der Division wird der Modulare Logarithmus betrachtet.
Dieses Verfahren ist dann unter den Namen ElGamal-Verschlüsselung bekannt.
Bisher kennt man keine Verfahren, die den Modularen Logarithmus einer
großen Zahl (mit mehr als 1000 Stellen) schnell bestimmen können. Alle
bisher bekannten Verfahren würden auf den schnellsten Rechnern dann
Jahrhunderte rechnen.
Selbst wenn diese also irgendwann die geheime Nachricht entschlüsseln, wird
die Fete längst vorbei sein.

Mittels anderer Operationen, z.B. elliptischer Kurven oder sogar hyper-elliptischer Kurven, ergeben sich noch weitere Verschlüsselungsverfahren. Viele Public-Key-Systeme benutzen den obigen Trick. Damit sieht man: der Trick ist sehr wichtig und mit diesem einfachen Trick kann man sehr viel erreichen.
Man fragt sich natürlich: Wie sicher sind die Verfahren? Zum einen muss man darauf achten, dass die verwendeten Zahlen groß genug sind. Wenn man zu kleine Zahlen wählt, dann kann es sein, dass ein Programm durch Ausprobieren den Schlüssel findet. Wenn nun der Schlüssel sehr groß ist, dann dauert das Ausprobieren auch sehr lange, z.B. Jahrhunderte. Damit ist das Geheimnis — z.B. der Fetentermin — ausreichend geschützt.
Kann es sein, dass jemand plötzlich ein Verfahren findet, den Modularen Logarithmus zu bestimmen? Bisher kann man noch nicht beweisen, dass es so ein Verfahren nicht gibt. Aber schon seit vielen Jahren versuchen Mathematiker und Informatiker für dieses Problem eine Lösung zu finden. Und bisher ist trotz aller Bemühungen keine Lösung gefunden worden. Man geht davon aus, dass es so ein Verfahren nicht gibt.
Wenn aber plötzlich doch ein schnelles Verfahren zur Lösung des
Modularen Logarithmus bekannt wird, dann ist die
Verschlüsselung nach ElGamal nicht mehr sicher.
Wir hoffen, dass das nicht passiert.
 Der obige Trick geht aber immer noch mit anderen
Operationen.
Der obige Trick geht aber immer noch mit anderen
Operationen.
- Dr. Dirk Bongartz
- PD Dr. Walter Unger

