Hagen Höpfner, International University in Germany Bruchsal
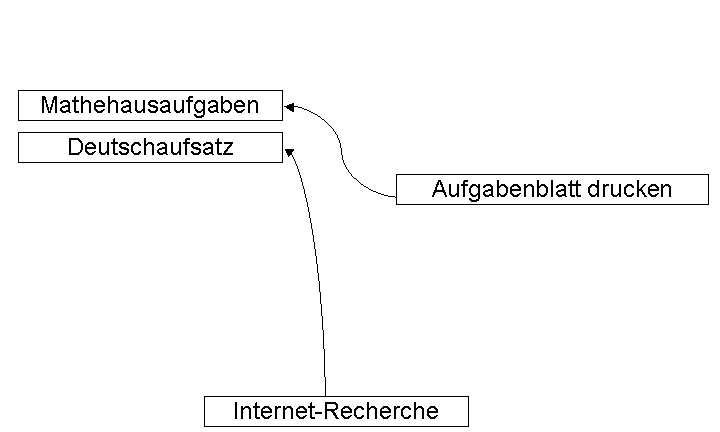
Wie soll ich das nur alles schaffen? Es sind zwar Ferien aber ich muss noch die Mathehausaufgaben machen. Dann ist da noch der Deutschaufsatz zu schreiben, wofür ich aber auch noch das Buch über die Geschichte der Informatik aus der Bibliothek holen und ein wenig im Internet recherchieren muss. Dabei fällt mir ein, dass auch der Computer nach der letzten LAN-Party noch nicht wieder aufgebaut und angeschlossen ist. Ganz nebenbei bemerkt dürften die Aufgabenblätter für die Mathehausaufgaben auch noch nicht ausgedruckt sein und in meiner Emailbox auf dem GMX-Emailserver schlummern. Dann ist heute abend auch noch eine Party, für die ich noch einen Sampler zusammenstellen und brennen wollte. Natürlich muss auf diese CD auch der neue Song von Placebo, den ich mir noch bei iTunes kaufen wollte. Als ob das noch nicht genug wäre hat mich meine Mutter zum Müllraustragen, Schuheputzen und Abwaschen eingeteilt und das, obwohl ich für die Party ja auch noch einen Kasten Cola aus dem Supermarkt aus der Stadt holen muss. Glücklicher Weise liegt der Supermarkt auf dem Weg zur Bibliothekt und das Spühlmittel zum Abwaschen ist ja ohnehin alle. Aber was erledige ich nun zuerst?

Hm, das Nacheinanderabarbeiten aller Punkte auf meiner ToDo-Liste macht
offensichtlich keinen Sinn. Schließlich kann ich die CD erst
brennen, wenn ich alle Songs habe und die bekomme ich nur zusammen,
wenn mein Rechner aufgebaut und ans Internet angeschlossen ist.
Irgendwie bestehen also Abhängikeiten zwischen den einzelnen
Aufgaben und noch nicht alle Teilaufgaben sind bisher aufgelistet.
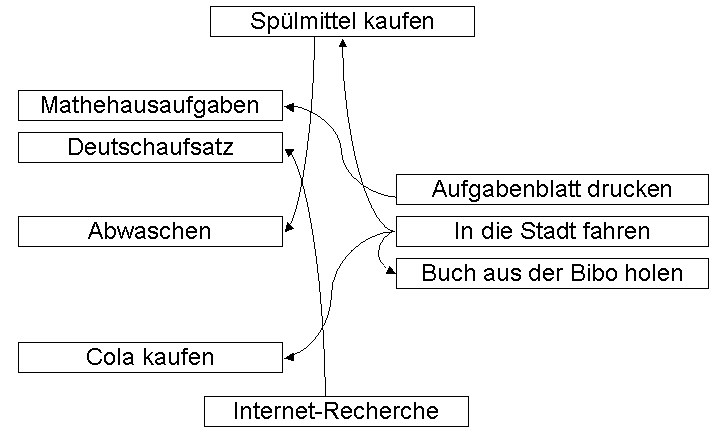
Darum nehme ich mir also einen Stift und vervollständige
zuerst einmal meine ToDo-Liste. Bevor ich abwaschen kann, muss ich
Spülmittel kaufen. Deshalb zeichne ich einen Pfeil von
"Spülmittel kaufen" zu "Abwaschen". Das Spülmittel bekomme
ich nur in der Stadt, weshalb ich einen Pfeil von "In die Stadt fahren"
zu "Spülmittel kaufen" zeichne usw.
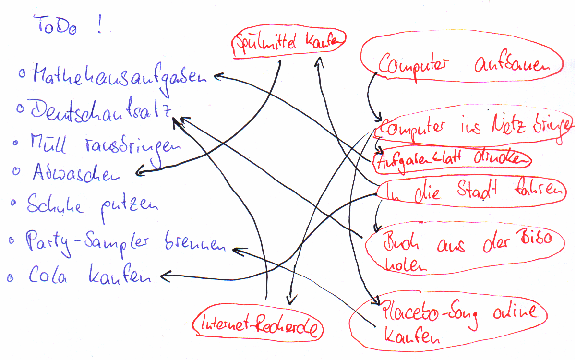
Mann, da wird einem erst mal richtig bewußt, was noch alles zu
tun ist, aber womit fange ich denn nun an? Ein Pfeil zeigt an,
dass irgendetwas nur dann erledigt werden kann, wenn zuvor etwas anderes
erledigt wurde. Also kann ich nur mit etwas anfangen, auf das kein
Pfeil zeigt. Zur Auswahl stehen in meinem Fall demnach:
- Müll rausbringen
- Schuhe putzen
- Computer aufbauen
- In die Stadt fahren
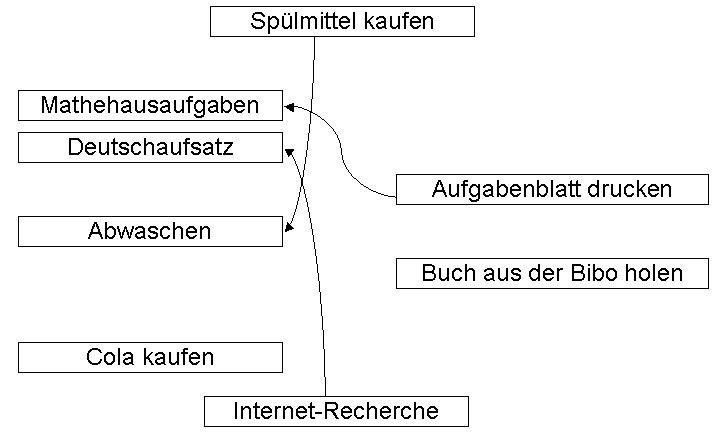
Eigentlich ist es ja egal, welche dieser vier Aufgaben ich als erstes in Angriff nehme. Aber ich bin mal nett und bringe den Müll raus, putze dann die Schuhe und baue erst anschließend den Computer auf. Nachdem ich das alles erledigt habe, kann ich meinen Aufgabenübersicht korrigieren und die erledigten Aufgaben abstreichen. Dadurch fallen natürlich auch etwaige Pfeile, die von erledigten Aufgaben ausgehen (hier von "Computer aufbauen" nach "Computer ins Netz bringen"), weg.
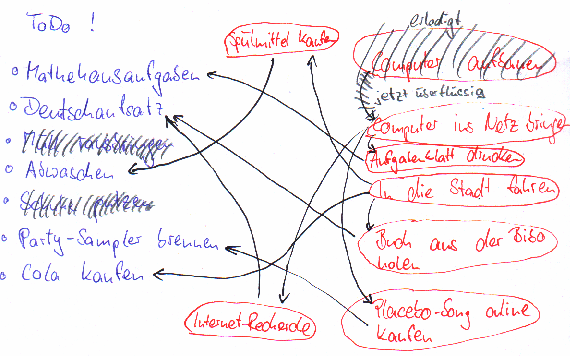
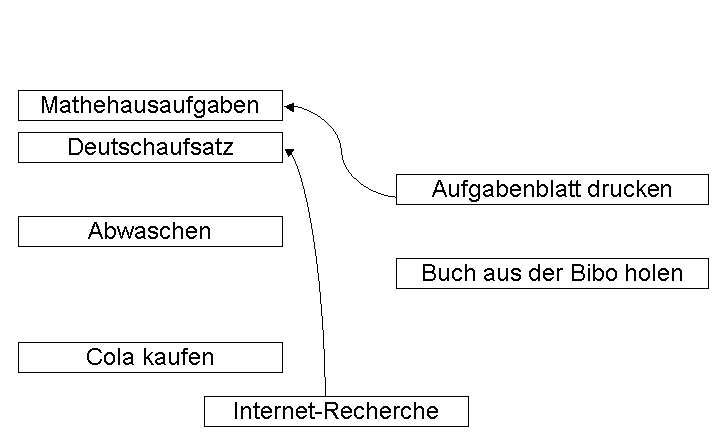
Doch was könnte ich als
nächstes tun? Nun, an der Tatsache, dass ich jetzt in die Stadt
fahren könnte hat sich nichts geändert. Da ich aber den Computer
inzwischen aufgebaut habe, kann ich ihn jetzt auch ins Netz bringen.
Schließlich habe ich den einzigen Abhängigkeitspfeil, der
auf die Aufgabe "Computer ins Netz bringen" gezeigt hat, soeben
"gelöscht". Alle anderen Aufgaben können noch nicht erledigt
werden. Da ich aber gerade am Rechner sitze, bringe ich ihn auch gleich ins
Netz.
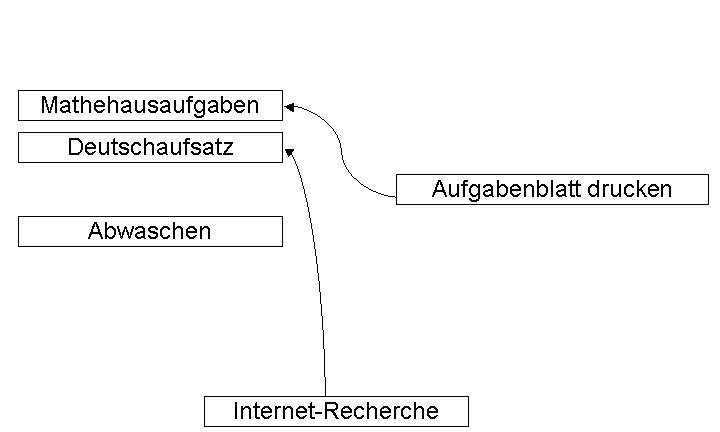
Dadurch ändert sich mein ToDo-Graph erneut.
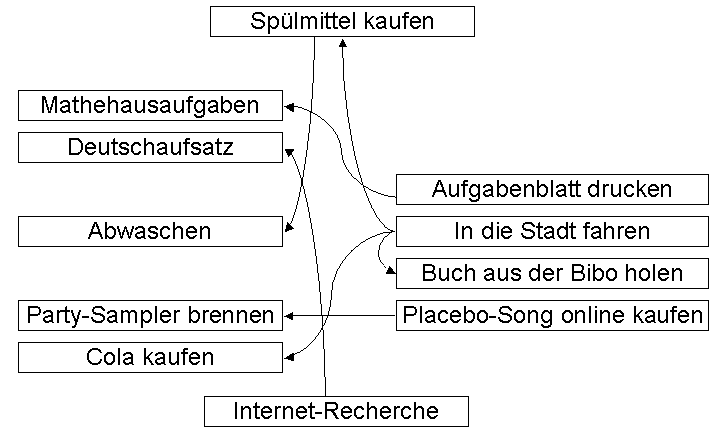
So, gleich geht es zur Party und ich wollte nur ganz kurz zusammenfassen, in welcher Reihenfolge ich meine Aufgaben heute erledigt habe:
- Müll rausgebracht
- Schuhe geputzt
- Computer aufgebaut
- Computer ins Netz gebracht
- Placebo-Song gekauft
- Party-Sampler gebrannt
- In die Stadt gefahren
- Spülmittel gekauft
- Cola gekauft
- Buch aus der Bibo geholt
- Abgewaschen
- Internet-Recherche erledigt
- Deutschaufsatz geschrieben
- Aufgabenblatt gedruckt
- Mathehausaufgaben gemacht
Mein großer Bruder, der Informatik studiert, hat mich gerade darüber aufgekärt, dass mein Vorgehen "topologisches Sortieren" genannt wird. Er hat mir auch die folgende Algorithmenbeschreibung geschenkt:
Der Algorithmus TopSort gibt die Knoten eines gerichteten Graphes in topologischer Reihenfolge aus. Der Graph G=(V,E) besteht hierbei aus der Menge der enthaltenen Knoten V und der Kantenmenge E der Form (Knoten1, Knoten2), wobei die Abhängigkeit von Knoten1 nach Knoten2 geht und beide Knoten auch in V vorhanden sein müssen.
Der Algorithmus erkennt auch, ob ein Graph zyklische Abhängigkeiten enthält. Derartige zyklische Graphen lassen sich nicht topologisch sortieren, daher muss bei jedem Schritt geprüft werden, ob auch tatsächlich ein Knoten entfernt wurde. Ist dies einmal nicht der Fall, so bricht der Algorithmus automatisch ab.
Das oben verwendete Beispiel verdeutlich auch ein wesentliches Problem
von Computern. Sie arbeiten normalerweise "stupide" ihre
Arbeitsschritte ab. Ziel von TopSort ist es, EINE
mögliche topologische Sortierung zu finden. Eine so bestimmte
gültige topologische Sortierung wäre z.B. auch:
- ...
- In die Stadt gefahren
- Spümittel gekauft
- Abgewaschen
- ...
- Cola gekauft
- ...
Hätten wir nicht nach dem "in die Stadt fahren" alle Einkäufe erledigt, dann hätten wir das Problem, dass wir später noch einmal in die Stadt fahren müssen, aber diese Information wurde dann ja schon aus dem Graph entfernt. Ein klein wenig Organisationstalent gehört also neben dem algorithmischen Abarbeiten einer Aufgabenliste auch noch dazu, wenn man seinen Alltag planen will.