Rolf Klein, Uni Bonn
Tom Kamphans, Uni Bonn
"There must be some way out of here," said the joker to the thief,
"There's too much confusion, I can't get no relief."
— Aus "All along the watchtower" von B. Dylan
„Oh weh - nun ist das Licht aus! Wie komme ich jetzt bloß hier heraus? War vielleicht doch keine gute Idee, allein in das Tunnelsystem unter den Kaiserthermen einzusteigen. Halt! Da war doch neulich was im Internet, wie man aus einem Labyrinth entkommt: Tiefensuche. Aber dazu brauchte man Licht und Kreide für Markierungen. Geht also nicht, bei dieser Finsternis. Muß ich etwa die Nacht hier verbringen?“
Was könnte man hier tun? Erst einmal vorsichtig der Nase nach gehen, bis man auf eine Wand trifft. Und dann mit der linken Hand immer an der Wand entlang. In diesem Labyrinth findet man so zum Ausgang:
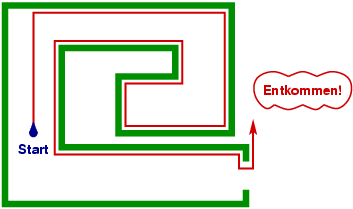 |
Aber wenn man auf eine Säule trifft, läuft man für immer im Kreis herum:
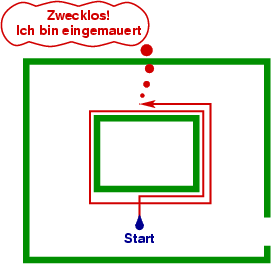 |
So geht es nicht! Man muß sich irgendwann wieder von solchen Säulen lösen. Also neuer Versuch: der Nase nach bis zur Wand, der Wand so lange folgen, bis man wieder in die alte Richtung schaut, und dann wieder der Nase nach. Jetzt macht die Säule keine Probleme mehr:
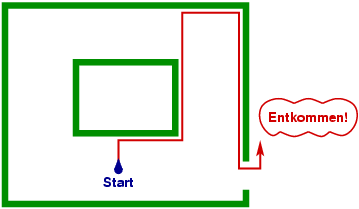 |
Aber dafür klappt's jetzt im ersten Beispiel nicht mehr:
 |
„Langsam wird es mir unheimlich! Was immer ich versuche, geht schief. Aber es muß doch einen Weg nach draußen geben - schließlich bin ich auch hereingekommen!“
Natürlich gibt es einen Weg nach draußen. Die Frage ist nur, wie er aussieht. Kann man wirklich einen allgemeinen Algorithmus angeben, der für jedes denkbare Labyrinth, aus dem es einen Ausweg gibt, einen Weg ins Freie findet? Und das auch im Dunkeln?
Erstaunlicherweise geht das tatsächlich. Es reicht aber nicht, nur auf die Richtung der Nase zu achten; man muß schon die Drehungen zählen, die unterwegs an den Ecken ausgeführt werden.
Angenommen, alle Ecken sind rechtwinklig, wie in unseren Beispielen. Dann kommen nur Rechtsdrehungen und Linksdrehungen um jeweils 90 Grad vor. Wir verwalten unterwegs einen Umdrehungszähler, der bei jeder Linksdrehung um eins erhöht und bei jeder Rechtsdrehung um eins erniedrigt wird (auch bei der ersten Rechtsdrehung, die nach dem Auftreffen auf eine Wand ausgeführt wird). Zu Beginn wird dieser Umdrehungszähler auf null gesetzt. Dann werden die beiden Anweisungen
geradeaus, bis Wand erreicht;
folge der Wand, bis Umdrehungszähler = 0;
Entdeckt haben soll diesen Algorithmus ein zwölfjähriger Junge namens John Pledge; deshalb nennt man ihn den Pledge-Algorithmus.
Er funktioniert nicht nur bei unseren beiden Beispielen, sondern immer!
Zum Beweis muß man sich folgendes überlegen: Wenn man mit dem Pledge-Algorithmus aus einem Labyrinth nicht herausfindet, so gerät man in eine Endlosschleife, die sich nicht selbst kreuzt.
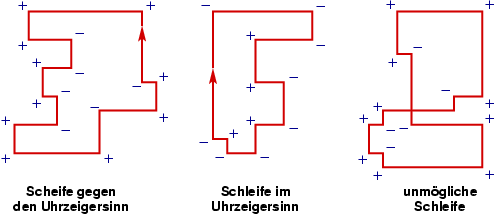
Würde sie gegen den Uhrzeigersinn durchlaufen, enthielte sie vier Linksdrehungen mehr als Rechtsdrehungen. Dann würde der Umdrehungszähler irgendwann positive Werte annehmen. Das kann aber nicht sein, denn nach dem Einschwenken zu einer Wand ist er zunächst bei -1, und sobald er den Wert 0 erreicht, verläßt man die Wand ja schon wieder! Folglich wird die Endlosschleife im Uhrzeigersinn durchlaufen. Bei jedem Durchlauf nimmt dann der Zähler um 4 ab, so daß er irgendwann nur noch negative Werte hat. Also folgt man mit der linken Hand ständig einer Wand, ohne sich je von ihr zu lösen. Dann gibt es aber auch gar keinen Weg nach draußen!
Dieser Film (geringe Auflösung (3,7MB), mittlere Auflösung (16,2MB), im Quicktime-Format) zeigt, wie ein Miniaturroboter des Typs Khepera II den Pledge-Algorithmus anwendet, um aus einem Schachtellabyrinth herauszufinden.
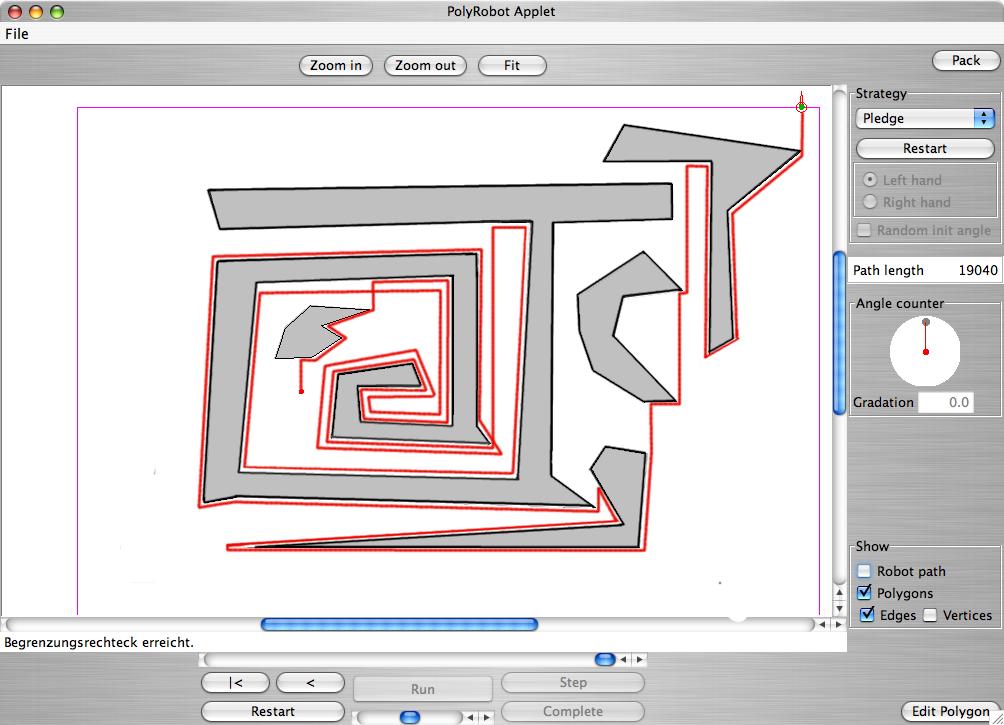
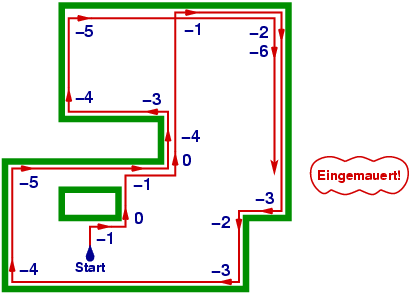
Wer mag, kann sich mit dem Java Applet http://www.geometrylab.de/Pledge/ selbst ein Labyrinth zeichnen und verfolgen, wie der Pledge-Algorithmus vorgeht. Er funktioniert übrigens auch, wenn die Ecken nicht rechtwinklig sind. Nur muß man dann statt des Umdrehungszählers einen Winkelzähler verwenden, in dem die Winkel mit Vorzeichen exakt aufaddiert werden. Hier ein Beispiel, das mit Hilfe des Java Applets erstellt wurde: