Algorithmus der Woche

• » Startseite
• » aktueller Algorithmus
• » Liste der Algorithmen

Informationen

• » Infoflyer Presse
• » Infoflyer Schule
• » Download Logo

Gimmicks für's Klassenzimmer

• » Visuelle Kryptographie

Links

• » Informatikjahr
• » Fakultätentag Informatik

Intern

• » Für Autoren
• » Für Organisatoren
• » Buchprojekt

Sonstiges

• » Impressum
• » Gästebuch
• » Haftung

Algorithmen sind clevere Verfahren, die Probleme verschiedenster Art effizient lösen. Wenn man Algorithmen genauer betrachtet, so könnte man vermuten, dass sie trotz aller Cleverness und Effizienz nur sture und gleich ablaufende Verfahren sind, die immer perfekte und eindeutige Lösungen liefern. Mit Zufall haben Algorithmen scheinbar nichts zu tun! Oder kann „zufälliges“ Verhalten programmiert werden? Kann „Zufall“ durch einen Algorithmus erzeugt werden? Antwort: Der Zufall wird mit Hilfe von Algorithmen nachgeahmt, die scheinbar zufällige Zahlen erzeugen. Diese Zahlen werden als Zufallszahlen oder genau genommen als Pseudo-Zufallszahlen bezeichnet. Wir betrachten hier eine Klasse von bekannten und altbewährten Algorithmen zur Erstellung von Zufallsgeneratoren. Für Zufallszahlen gibt es zahlreiche Anwendungsbereiche; hier werden wir zwei davon kennen lernen: Ein Computerspiel und die so genannte Monte-Carlo-Simulation zur Flächenberechnung.

Die Rolle des Zufalls in Computerspielen

Algorithmen, bei denen Zufall sehr erwünscht oder sogar notwendig ist, kennen wir alle aus dem Bereich der Taktik- und Strategiespiele. Der Rechner übernimmt oft die Rolle eines Gegenspielers, wobei die Aktionen von Algorithmen gesteuert werden, die sinnvolle und intelligente Verhaltensvariationen erzeugen sollen. Wir kennen das von interaktiven Computerspielen wie Siedler, SimCity, Doom, Counterstrike oder Warcraft. Natürlich soll der Rechner bei gleichen Situationen nicht immer auf die gleiche Art reagieren, sondern es sollen unterschiedliche Effekte und Aktionen erzeugt werden. Dadurch kommt mehr Abwechslung und Spannung ins Spiel.

Ein Taktikspiel: Schnick-Schnack-Schnuck

Als einfaches Beispiel für ein programmiertes Spiel können wir uns überlegen, wie ein Algorithmus für das bekannte Spiel „Papier-Schere-Stein“ (Schnick-Schnack-Schnuck) aussehen könnte. Das Spiel funktioniert so: Bei jeder Spielrunde wählst Du eine der drei Möglichkeiten „Papier“, „Schere“ oder „Stein“.

Drei Möglichkeiten: Papier, Schere oder Stein?

Dann wird der Algorithmus ausgeführt und liefert als Ergebnis ebenfalls „Papier“ oder „Schere“ oder „Stein“. Danach wird ausgewertet. Es gewinnt Papier gegen Stein, Stein gegen Schere und Schere gegen Papier. Der Sieger bekommt einen Punkt; danach folgt die nächste Spielrunde.

Wie soll der Algorithmus arbeiten? Soll zum Beispiel abwechselnd „Schere“ und „Stein“ gewählt werden? Das wird der menschliche Spieler schnell durchschauen! Das Ergebnis des Algorithmus muss also unvorhersehbar sein, so wie das Werfen eines Würfels, das Ziehen der Lottozahlen oder der Lauf einer Roulette-Kugel.

Münze: Kopf oder Zahl	Würfel: 1, 2, 3, 4, 5 oder 6	Rouletterad: 0, 1, ..., 36

Die mechanische Kopplung eines Algorithmus mit einem Würfel oder einem Rouletterad wäre ziemlich umständlich, jedenfalls wäre eine solche Konstruktion nicht effizient und auch nicht clever. Gebraucht wird deswegen ein algorithmisches Verfahren, welches unter den Möglichkeiten „Papier“, „Schere“ oder „Stein“ eine scheinbar zufällige Wahl trifft. Solch ein Algorithmus heißt „Zufallsgenerator“ oder auch „Zufallszahlengenerator“.

Hilfsmittel zur Erzeugung von Zufallszahlen: Modulo-Rechnung

Bevor wir uns mit der Berechnung von Zufallszahlen näher beschäftigen, benötigen wir das Konzept der Modulo-Rechnung. Die Modulo-Funktion (auch mod-Funktion genannt) bestimmt den Rest, der bei der Divison zweier natürlicher Zahlen entsteht. Teilen wir zum Beispiel die Zahl 27 durch 12 so bleibt als Rest die Zahl 3.

Betrachten wir zwei beliebige natürliche Zahlen x und m und dividieren x durch m, dann erhalten wir einen (ganzzahligen) Quotienten a und einen Rest r. Dieser Rest ist eine natürliche Zahl zwischen 0 und m-1. Man verwendet die Sprechweise: „Die Zahl x ist kongruent zu r modulo m“; in Kurzschreibweise x ≡ r (mod m).

Einige Beispiele zur Modulo-Rechnung

9 ≡ 1 (mod 8): 9 ist kongruent 1 modulo 8, weil 9 bei Division durch 8 den Rest 1 ergibt.
16 ≡ 0 (mod 8): 16 ist kongruent 0 modulo 8, weil 16 ohne Rest durch 8 teilbar ist.
9+6 = 15 ≡ 3 (mod 12)
6*2 + 15 = 27 ≡ 3 (mod 12)
1143 ≡ 143 (mod 1000): Bei Division durch 1000 besteht der Rest aus den letzten 3 Stellen

Veranschaulichung der Modulo-Rechnung

Wir können uns die Modulo-Rechnung wie das Wandern entlang eines Kreises vorstellen, auf dem die Zahlen 0, 1, 2, ..., m-1 aufgetragen sind. Um x modulo m, also den Rest von x bei der Division durch m zu bestimmen, starten wir bei 0 und gehen dann in Einerschritten nach rechts. Die Anzahl der Umrundungen des Kreises ist gegeben durch das Ergebnis der ganzzahligen Division a; die Zahl, bei der wir landen, ist der Rest r.

Startet man z.B. eine Stundenzählung mit einer Analoguhr am 1. Januar um 0 Uhr, dann sind am 2. Januar um 19 Uhr zwar 43 Stunden vergangen, aber der Stundenzeiger Uhr zeigt auf 7 Uhr, das ist der Rest r ≡ 43 mod 12. Eine Analoguhr zeigt die Stunden modulo 12 an, dies ist der Rest, der sich bei der Division der vergangenen Stunden durch 12 ergibt. Eine Addition entspricht einer Bewegung in Uhrzeigerrichtung.

Betrachten wir zwei Beispiele (vgl. die beiden Bilder):

Linkes Bild: Starten wir zum Beispiel bei x=9 und addieren 6, dann bewegen wir uns 6 Schritte in Uhrzeigerrichtung und erreichen die 3, d.h. es gilt 9+6 ≡ 3 (mod 12).

Rechtes Bild: Die Multiplikation einer Zahl x mit einem Faktor a kann man sich als eine Folge von Additionsschritten vorstellen; starten wir z.B. bei dem Wert x=2, und multiplizieren mit a=6, dann addieren wir 5-mal den Wert 2, machen also 5 Zweierschritte im Uhrzeigersinn und erreichen den Wert 0, d.h. es gilt 6*2 ≡ 0 (mod 12).

Die Modulo-Arithmetik ist in der Informatik die „natürliche“ Arithmetik, weil Rechner einen begrenzten (= endlichen) Speicher haben und auch die Speicherzellen nur endlich groß sind und deswegen Zahlen nur bis zu einer bestimmten Größe gespeichert werden können.

Ein Algorithmus zur Erzeugung von Pseudo-Zufallszahlen

Der folgende Algorithmus erzeugt Zufallszahlen aus dem Intervall [0, m-1], wobei wir die Modulo-Rechnung verwenden. Das Grundprinzip ist einfach: Wir nehmen einen Startwert x, führen eine kleine Rechnung der Form a*x+c aus, und berechnen den Rest r durch r = a*x+c (mod m). Das Ergebnis ist die erste Zufallszahl x₁=r. Wir verwenden x₁ als neuen Ausgangswert und berechnen die zweite Zufallszahl x₂. Dadurch ergibt sich eine Folge von Zufallszahlen x₁, x₂, x₃, ... .

Diesen Algorithmus für einen Zufallszahlengenerator können wir auch so aufschreiben:

x₁ := a*x₀ + c (mod m)
x₂ := a*x₁ + c (mod m)
x₃ := a*x₂ + c (mod m)
x₄ := a*x₃ + c (mod m)
... usw ...

In allgemeiner Schreibweise erhalten wir die iterative Rechenvorschrift:

x_i+1 := a*x_i + c (mod m), i = 0, 1, 2, … .

Um ein konkretes Beispiel für einen Zufallszahlengenerator festzulegen, müssen wir die Parameter a, c, m und den Startwert x₀ festlegen. Mit den Festlegungen a=5, c=1, m=16 und dem Startwert x₀=1 ergibt sich folgende Rechnung.

x₁ := 5* 1 + 1 (mod 16) = 6
x₂ := 5* 6 + 1 (mod 16) =15
x₃ := 5*15 + 1 (mod 16) =12
x₄ := 5*12 + 1 (mod 16) =13
x₅ := 5*13 + 1 (mod 16) = 2
x₆ := 5* 2 + 1 (mod 16) =11
x₇ := 5*11 + 1 (mod 16) = 8
x₈ := 5* 8 + 1 (mod 16) = 9

... usw. …

Wir haben also eine Zahlenfolge 6, 15, 12, 13, 2, 11, 8, 9, … erzeugt, die wir mit etwas gutem Willen als „Zufallszahlen“ akzeptieren können.

Periodisches Verhalten

Rechnen wir weiter, dann fällt auf, dass wir nach 16 Schritten wieder bei dem Ausgangswert 1 ankommen, und dass jede der 16 möglichen Zahlen 0, 1, 2, …, 15 genau einmal vorkommt. Berechnet man die Werte für x₁₆, x₁₇, …, x₃₁ dann wiederholt sich die Zahlenfolge. Wir sehen also ein periodisches Verhalten, hier mit der Periode 16. Wenn wir m sehr groß wählen und außerdem den Faktor a und die Konstante c geschickt festlegen, dann erhalten wir größere Perioden, im Idealfall erhält man die volle Periode der Länge m. In Programmiersprachen sind manchmal Zufallszahlengeneratoren fest „eingebaut“ oder über eine „Bibliothek“ von Funktionen verwendbar; zum Beispiel gibt es in der Programmiersprache Java einen vollperiodigen Generator mit den Parametern a=252149003917, c=11 und m=2⁴⁸.

Simulation von echten Zufallsgeneratoren

Die Erzeugung von Pseudozufallszahlen aus dem Bereich 0, 1, …, m-1 ist die Grundlage für viele Anwendungen. Beispiele sind die Simulation eines Münzwurfs mit den Ergebnissen Kopf oder Zahl, das Werfen eines Würfels mit den Ergebnissen 1, 2, 3, 4, 5 und 6 oder das Drehen eines Rouletterads mit den 37 Möglichkeiten 0, 1, …, 36.

Nehmen wir an, dass es bei allen Beispielen fair zugeht, d.h. die Wahrscheinlichkeit für Kopf bzw. Zahl ist jeweils 1/2, beim Würfel haben wir 1/6 und beim Roulette 1/37. Zur Simulation des Münzwurfs benötigen wir also ein Verfahren zur Umwandlung einer Zufallszahl x aus {0, 1, …, m-1} in eine Zahl z ∈ {0, 1}, wobei 0 für „Kopf“ und 1 für „Zahl“ stehen soll. Ein einfaches Verfahren wäre eine Rechnung mod 2, d.h. z ≡ x (mod 2); wodurch die Zahl x in 0 oder 1 umgewandelt wird.
Beim Roulette hätten wir eine Transformation z ≡ x (mod 37) und beim Würfel z ≡ x (mod 6) +1.

Der Schnick-Schnack-Schnuck-Algorithmus

Jetzt endlich zurück zu unserem „Taktikspiel“. Wir benötigen einen Algorithmus, der unter den drei Möglichkeiten „Papier“, „Schere“ oder „Stein“ eine Zufallsauswahl trifft. Zu diesem Zweck verwenden wir einen Zufallszahlengenerator, mit dem wir bei jeder Spielrunde eine Zufallszahl x erzeugen und daraus durch z ≡ x (mod 3) eine neue Zahl bestimmen, die nur die drei Werte 0, 1 und 2 annehmen kann. Abhängig vom Wert von z wählt der Algorithmus „Papier“(0), „Schere“(1) oder „Stein“(2). Dieser Algorithmus ist in einem kleinen Programm implementiert, dem „Schnick-Schnack-Schnuck-Applet“.

Es stehen vier Zufallszahlengeneratoren (ZZG) zur Auswahl.

1) Deterministisch: Die feste Zahlenfolge 2 0 1 1 0 0 0 2 1 0 2
2) ZZG-016: a=5, c=1, m=16 und Startwert x₀ =1 (Periode 16)
3) ZZG-100: a=81, c=1, m=100, Startwert x₀ =10 (Periode 100)
4) Java-Generator: Der in der Programmiersprache Java vorgegebene Generator „Random“

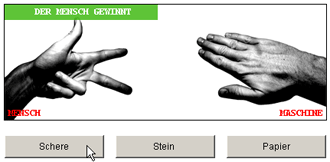
Die Bilder zeigen den Spielverlauf. „Mensch“ und „Maschine“ wählen gleichzeitig Schere, Stein oder Papier. Die Tabellen zeigen den Spielstand und den Ablauf des Algorithmus.

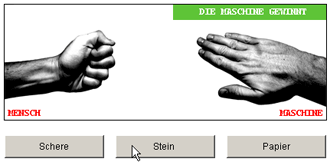Schere schneidet Papier	Stein wird von Papier eingewickelt

Spielstand nach 3 Runden: Mensch - Maschine 2:1

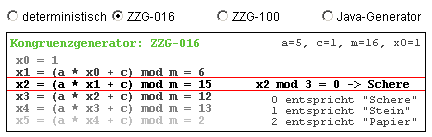Algorithmus der Maschine

In der vorstehenden Tabelle kann man die Arbeit des ausgewählten Zufallsgenerators beobachten (ausgewählt ist hier ZZG-016). Der aktuelle Rechenschritt ist hervorgehoben; aber auch die zukünftigen Werte sind bereits sichtbar! Man kann also feststellen, was die Maschine als nächstes tun wird. (Ein kleiner „Cheat“!).

Das Applet läuft im Browserfenster ab (Java muss aktiviert sein).

Monte Carlo-Simulation: Flächenberechnung mit „Zufallsregen“

Ein wichtiger Anwendungsbereich von Zufallszahlen ist die sog. Monte-Carlo-Simulation, die nach dem Spielcasino in Monte Carlo benannt ist. Monte-Carlo-Simulation kann z.B. verwendet werden, um eine Flächenbestimmung von unregelmäßigen geometrischen Figuren durch sog. „Zufallsregen“ durchzuführen. Von Zufallsregen spricht man, wenn viele zweidimensionale Zufallspunkte (x,y) auf eine Ebene treffen. Ein Zufallspunkt in der Ebene wird durch ein (x,y)-Paar von zufälligen Koordinatenwerten bestimmt, wobei der x-Wert und der y-Wert jeweils durch eine Zufallszahl aus dem Intervall (0,1) festgelegt werden.

Legt man diese unregelmäßige Fläche in ein Quadrat mit Kantenlänge 1, und wirft Zufallspunkte in dieses Quadrat, dann fällt ein Teil der Punkte auf diese Fläche und der Rest daneben.

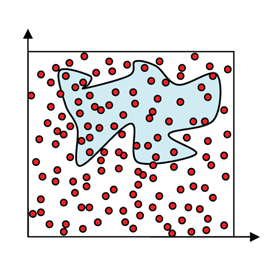Zwei Zufallspunkte (x1, y1) und (x2, y2)	Zufallsregen: Zähle die Treffer auf der Fläche

Eine Schätzung für den Flächeninhalt erhält man durch die Berechnung des Quotienten F=Trefferanzahl/Punkteanzahl. Um eine gute Schätzung zu bekommen, muss man Millionen oder sogar Milliarden von Punkten werfen. Eine Durchführung dieses Algorithmus von Hand wird man deswegen niemanden zumuten, aber für einen programmierten Algorithmus auf einem Rechner ist es natürlich kein Problem, eben mal 1 Million Zufallspunkte in ein Quadrat zu werfen!

Als Illustration, wie man Monte-Carlo-Simulation praktisch verwenden kann, betrachten wir ein Verfahren zur Bestimmung der berühmten Kreiszahl π = 3,14159… .
Eine näherungsweise Bestimmung der Zahl kann durch das "Werfen" von zufälligen Punkten (x,y) in den Einheitskreis durchgeführt werden. Wir betrachten ein Quadrat mit Seitenlänge 1 (Fläche = 1), wobei im I. Quadranten ein Viertelkreis eingebettet ist. Da der Kreis den Radius r=1 hat, ist seine Fläche F = r²π = π und die Fläche des Viertelkreises ist π/4.

Wie viele Zufallspunkte fallen in den Kreis?

Sei die Zahl der Treffer T im Viertelkreis und die Gesamtzahl der Würfe N in dem Quadrat, dann können wir näherungsweise berechnen durch π ≈ 4*T/N. In dem Bild sind 130 Zufallspunkte dargestellt, davon fallen 102 in den Viertelkreis, d.h. wir rechnen π ≈ 4*102/130 ≈ 3.1384. Das ist noch kein sehr guter Wert für π, aber mit 100000 oder 1 Million oder sogar 1 Milliarde Punkten sollte das Ergebnis wesentlich genauer werden.

Es gibt zahlreiche Anwendungen der Monte-Carlo-Simulation in der numerischen Mathematik, den Naturwissenschaften, der Technik und der Finanzwissenschaft.