Autor
Martin Dietzfelbinger, Technische Universität Ilmenau

Alice und Bob sind dicke Freunde. Alice wohnt in Adelaide in Australien und Bob in Barnsley in (Groß-)Britannien. Sie telefonieren gerne miteinander, was aber ganz schön ins Geld geht, wenn es länger dauert. Die beiden haben sehr ähnliche Interessen; da ist es kein Zufall, dass sich beide ein Lexikon anschaffen.
Sogar wenn Alice und Bob feststellen, dass beide z.B. die 10. Auflage des Lexikons besitzen, muss das nicht unbedingt heißen, dass in dem in Australien gedruckten Exemplar wortwörtlich derselbe Text steht wie in dem in England gedruckten. Vielleicht wurden irgendwelche Druckfehler ausgebessert? Was tun? Alice könnte Bob ihr Lexikon vorlesen. Bob würde mitlesen und Wort für Wort vergleichen. Das würde theoretisch funktionieren, aber höllisch Telefongebühren kosten, denn ...
Wir können in einem Computer ein Schriftzeichen (auch die Kommas und Zwischenräume) mit einem Binärcode darstellen, zum Beispiel mit 8 Bits, d.h. 1 Byte, pro Zeichen. Macht für das Lexikon 50 Millionen Bytes, oder etwa 50 Megabytes (MB). Alice könnte nun natürlich ihr Lexikon in den Computer eintippen oder einscannen oder die Textkopie auf der mitgelieferten CD benutzen und Bob die Datei per Email schicken. Das finden wir aber gemogelt, und bestehen (im Jahr 2006 ein bisschen künstlich) darauf, dass Botschaften mündlich übermittelt werden, und dass Telefonieren Geld kostet. Computer darf man aber natürlich benutzen.
Die Frage ist also: Können Alice und Bob feststellen, ob die beiden Texte gleich sind, ohne sie Wort für Wort zu vergleichen?
Wer öfter große Dateien per Email verschickt oder auf seiner knallvollen Festplatte Platz schaffen musste, hat vielleicht schon einmal etwas von „Datenkompression“ gehört. Das sind Methoden, mit denen man Daten wie Texte oder Bilder „zusammenquetscht“, um Übertragungszeiten zu verkürzen und um Speicherplatz zu sparen. Alice und Bob könnten solche Methoden benutzen. Aber sogar wenn sie eine Komprimierung auf ein Fünftel der ursprünglichen Länge bewerkstelligen könnten, wären dies immer noch 10 Millionen Zeichen, die Alice übermitteln müsste. Das ist den beiden einfach zu viel.
Wie sollen Alice und Bob es anstellen, um mit noch weniger Kommunikation auszukommen?
Eine ganz einfache Beobachtung: Alice sollte zunächst die Buchstaben in ihrem Lexikon zählen. Diese Anzahl wollen wir n nennen. Alice sagt Bob, was n ist (das sind 8 Dezimalziffern, also kein Problem). Bob hat inzwischen die Buchstaben in seinem Lexikon gezählt, Resultat n'. Wenn n und n' verschieden sind, haben die Lexika verschiedene Texte, und wir sind fertig. (Wir wollen mal annehmen, dass Alice und Bob sich nicht verzählen.) Ab hier sind also die Texte, die wir vergleichen wollen, auf jeden Fall gleich lang.
Eine wie lange Nachricht muss Alice nun übermitteln?
Bevor wir diese Frage beantworten können, müssen wir etwas technischer werden und uns ein bisschen Handwerkszeug zurechtlegen. Wir haben schon gesagt, dass man Buchstaben im Computer mit Bitmustern (Bytes) darstellt. Hier benutzen wir eine Standard-Darstellung, den ASCII-Code. In dieser Darstellung sehen A, B, C so aus: 01000001, 01000010, 01000011, und so weiter. Diese Bitmuster kann man auch als Zahlen auffassen, zum Beispiel:
| A | B | C | ... | Z | a | b | ... | z |
| 65 | 66 | 67 | ... | 90 | 97 | 98 | ... | 122 |
Auch die Satzzeichen bekommen Nummern, z.B. hat das Ausrufezeichen die Nummer 33 und ein Zwischenraum die Nummer 32. Mit 8 Bits bekommt man Zahlen zwischen 0 und 255. Der Text
wird, inklusive Zwischenräumen und Punkt, in die Folge
übersetzt, die wir mathematisch als
von Zahlen zwischen 0 und 255 übersetzt hat und dass Bob das gleiche mit seinem Lexikon gemacht hat:
Dabei ist n ungefähr 50 Millionen.
So lange Folgen können wir auf dieser Webseite natürlich nicht aufschreiben. Wir nehmen als Beispiel erst einmal zwei Folgen der Länge n=8: die Folge für „Adelaide“ (weil das auch ziemlich weit vorne im Lexikon steht):
und die Folge für „Barnsley“:
Nun müssen wir uns an einen Trick erinnern: „modulare Arithmetik“. (Siehe den 13. Algorithmus der Woche über „Fehlererkennende Codes“.) Das heißt, dass man ganze Zahlen nimmt und immer den Rest bei der Division durch m ausrechnet, bzw. zählt, wieviele Schritte man auf der Zahlengeraden nach links gehen muss, bis man auf ein Vielfaches von m trifft. Wenn zum Beispiel m=7 ist, hat man 16 mod 7 = 2 und -4 mod 7 = 3. In der folgenden Tabelle sind noch mehr Werte aufgeschrieben. Man erkennt das Muster: es geht immer im Kreis herum.
| a | ... | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a mod 7 | ... | 3 | 4 | 5 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | 1 | 2 | 3 | ... |
Man kann Zahlen „modulo m“ auch addieren und multiplizieren. Das heißt: man addiert und multipliziert ganz normal und rechnet vom Ergebnis den Rest bei der Division durch m aus. Um sich die Arbeit zu erleichtern, darf man bei längeren Rechnungen auch unterwegs Zwischenergebnisse immer durch ihren Rest ersetzen.
Nun zurück zu unseren Beispieltexten TAd und TBa. Wir legen eine Zahl m fest. Später werden wir sehen, dass m eine Primzahl sein sollte, die größer als 255 und größer als n ist, vielleicht etwa so groß wie 2n oder 10n.
Für unser Beispiel wählen wir m=17.
Für r = 0, 1, 2, ..., m-1 und einen Text T = ( a1 , a2 , ... , an-1 , an ) sehen wir die folgende Zahl an:
Zum Beispiel bekommen wir für TAd und r=3:
Wir nennen FP(T,r) einen „Fingerabdruck“ (engl.: „Fingerprint“) für den Text T = ( a1 , a2 , ... , an ) (mit r berechnet), weil in der Zahl FP(T,r) auf kleinem Raum eine gewisse Information über T gespeichert ist, die wir vielleicht nutzen können, um T von anderen Texten zu unterscheiden, so wie ein kleiner Fingerabdruck genügt, um Menschen zu unterscheiden. Ein ganz primitiver „Fingerabdruck“ ist natürlich auch die Länge n des Textes.
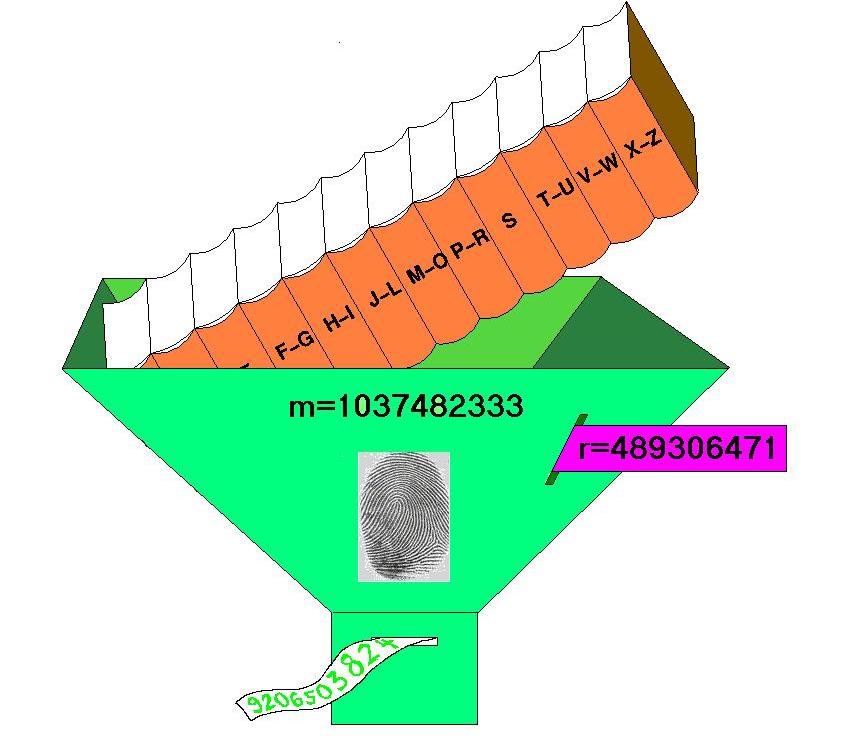
Die Berechnung von FP(T,r) sieht, besonders für die langen Texte, die uns eigentlich interessieren, ziemlich gefährlich und teuer aus, weil durch die hohen Potenzen riesengroße Zahlen entstehen. Hier hilft ein recht einfacher Trick, nämlich Umklammern:
Wenn man diesen Ausdruck wie üblich von innen nach außen fortschreitend ausrechnet, und „unterwegs“ bei jedem Zwischenergebnis den Rest „modulo m“ bildet, kann man die Zwischenergebnisse klein halten, ganz egal wie groß n ist. Im Beispiel, mit r=3, ergibt sich:
| Werte | Zwischenergebnis | |
|---|---|---|
| a1 | 65 | (65 · 3) mod 17 = (14 · 3) mod 17 = 8 |
| a2 | 100 | ((8 + 100) · 3) mod 17 = (6 · 3) mod 17 = 1 |
| a3 | 101 | ((1 + 101) · 3) mod 17 = (0 · 3) mod 17 = 0 |
| a4 | 108 | ((0 + 108) · 3) mod 17 = (6 · 3) mod 17 = 1 |
| a5 | 97 | ((1 + 97) · 3) mod 17 = (13 · 3) mod 17 = 5 |
| a6 | 105 | ((5 + 105) · 3) mod 17 = (8 · 3) mod 17 = 7 |
| a7 | 100 | ((7 + 100) · 3) mod 17 = (5 · 3) mod 17 = 15 |
| a8 | 101 | ((15 + 101) · 3) mod 17 = (14 · 3) mod 17 = 8 |
Also ist FP( TAd , 3 ) = 8.
Natürlicherweise ist der Fingerabdruck selber immer ein Rest modulo m, also eine Zahl zwischen 0 und m-1, und auch die Zwischenresultate bei der Berechnung sind nicht allzu groß (nicht größer als m2).
Wie rechnet man also einen Fingerabdruck FP(T,r) aus?
Algorithmus FP(T,r)
Mit diesem Programm rechnen wir spaßeshalber einmal alle m=17 Fingerabdrücke für TAd und für TBa aus.
| r | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FP( TAd , r ) | 0 | 12 | 7 | 8 | 11 | 14 | 15 | 5 | 11 | 1 | 2 | 12 | 13 | 13 | 6 | 6 | 0 |
| FP( TBa , r ) | 0 | 16 | 9 | 2 | 2 | 6 | 14 | 3 | 11 | 12 | 2 | 10 | 11 | 15 | 2 | 10 | 11 |
(Alice könnte die erste Zeile ausrechnen, Bob die zweite.) Wir vergleichen die Werte für TAd und TBa. Bei r=0 steht da in beiden Zeilen 0, ach ja, ist ja klar, im Algorithmus FP ist die letzte Aktion eine Multiplikation mit r, und wenn r=0 ist ... Ein Fingerabdruck mit r=0 ist also langweilig. Sonst sehen die Zahlen ziemlich wirr aus. Wir vergleichen übereinander stehende Zahlen. Bei r=3 (unser Beispiel) ist FP( TAd , r ) = 8 und FP( TBa , r ) = 2. Der Fingerabdruck mit r=3 würde also helfen zu sagen, dass die Texte verschieden sind. Bei r=8 und bei r=10 kommt aber derselbe Wert heraus (11 bzw. 2), diese r's helfen also nicht.
Jetzt kommt die entscheidende Idee. Nehmen wir einmal an, Alice und Bob machen sich überhaupt nicht die Mühe, alle Werte in der Tabelle auszurechnen. (Bei größeren n und m geht das sowieso aus Zeitgründen nicht.) Alice wählt aber eine Zahl r zwischen 1 und m-1 zufällig. Sie könnte zum Beispiel wiederholt ein „Glücksrad“ drehen, dessen Rand in zehn gleichgroße Teile unterteilt ist, um die Dezimalziffern von r zu bestimmen.
- 1. Fall:
- Die Texte TA und TB sind gleich. Dann erhalten Alice und Bob immer die gleichen Resultate, ganz egal, welches r Alice gewählt hat.
- 2. Fall:
- Die Texte TA und TB sind verschieden (im Beispiel „Adelaide“ und „Barnsley“ bei m=17).
- Wenn Alice eine Zahl r mit FP( TA , r ) = FP( TB , r ) gewählt hat (im Beispiel: „r=8“ oder „r=10“), dann bekommt Bob denselben Fingerabdruck wie Alice heraus, und es sieht für die beiden so aus, als könnten die Texte gleich sein.
- Wenn Alice eine Zahl r mit FP( TA , r ) ≠ FP( TB , r ) gewählt hat (im Beispiel: eine der anderen 14 Zahlen), dann bekommt Bob einen anderen Fingerabdruck heraus und er kann Alice mitteilen, dass die Texte auf jeden Fall verschieden sind.
In unserem kleinen Beispiel ist die Chance, dass der Unterschied gefunden wird, 14 : 16, also 87,5 Prozent.
Wie stehen die Chancen, einen Unterschied zu finden, im allgemeinen Fall?
Man kann beweisen (tatsächlich ist das schon seit mehreren hundert Jahren bekannt), dass folgendes passiert:
Fingerprinting-Satz:
Wenn TA und TB verschiedene Texte (Zahlenfolgen) der Länge n sind,
und wenn m eine Primzahl ist, die größer ist als die größte Zahl in TA und TB ,
dann können von den m Zahlenpaaren
Dieser Satz ist eine der einfacheren der vielen wunderbaren Eigenschaften, die Primzahlen haben. (Wer mehr darüber wissen will, warum das so ist, möge sich die Zusatzinformationen des Autors ansehen.)
Für unser Beispiel mit n=8 heißt das: Ganz egal wie TA und TB aussehen: wenn sie verschieden sind, gibt es in unserer Tabelle nie mehr als 7 Werte r ≠ 0, die Alice und Bob zum selben Ergebnis führen. Die Chance, dass der Unterschied gefunden wird, ist also immer mindestens 9 : 16, also mehr als 50 Prozent.
Nun kehren wir zur Anfangssituation zurück: n≈50 Millionen. Damit jetzt etwas Vernünftiges herauskommt, müssen Alice und Bob m um einiges größer als n wählen, sagen wir: m ist eine Primzahl etwas größer als 1 Milliarde, z.B. m=1037482333. Für so große n und m können und wollen wir die Tabelle der FP(T,r)-Werte bestimmt nicht mehr aufschreiben. Dennoch können wir sagen: Unter den m-1 Spalten gibt es höchstens n viele, wo die Werte übereinstimmen. Also: Wenn Alice r zwischen 1 und m-1 zufällig wählt und Alice und Bob rechnen und sich Zahlen und Fingerabdrücke mitteilen wie vorher, dann ist die Chance, dass sie den Unterschied zwischen verschiedenen Texten TA und TB entlarven, mindestens
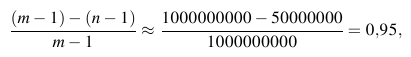
Alice und Bob müssen zwar viel rechnen — das lassen sie ihre Computer machen — , aber sie müssen nicht viel Information austauschen: Alice muss Bob die Zahl n (8 Ziffern) und die Primzahl m nennen (10 Ziffern), und sie muss ihm die beiden Zahlen r und FP( TA , r ) vorlesen (20 Ziffern).
Alice muss Bob weniger als 40 Ziffern mitteilen!
Wenn man mit einer Chance auf Entlarvung von unterschiedlichen Texten von 95 Prozent nicht zufrieden ist, gibt es eine auch nicht allzu teure Verbesserungsmöglichkeit: Alice wählt zwei Zahlen r1 und r2 zufällig und nennt Bob diese beiden und die Werte FP( TA , r1 ) und FP( TA , r2 ). Bob erklärt die beiden Texte für gleich (wobei er sich irren kann), wenn für TB bei r1 und r2 dieselben Zahlen herauskommen. Die Chance, dass die beiden hier irrtümlich zwei verschiedene Texte für gleich halten, ist höchstens

Wir fassen das Rechen- und Kommunikationsverfahren nochmals zusammen. Da es um eine Kombination von Berechnungen und Kommunikation geht, spricht man nicht von einem Algorithmus, sondern von einem „Protokoll“ (im Sinne einer Vorschrift darüber, wie sich die Beteiligten verhalten sollen).
Protokoll Textvergleich mit Fingerprinting
Alice hat Zahlenfolge TA = ( a1 , ... , an ) mit Ziffern zwischen 0 und d-1.
Bob hat Zahlenfolge TB = ( b1 , ... , bn' ) mit Ziffern zwischen 0 und d-1.
- Alice sagt Bob, was n ist. Wenn n ≠ n' ist, sagt Bob „ungleich“, und STOP.
- Alice und Bob einigen sich auf eine Wiederholungsanzahl k.
- Alice sucht eine Primzahl m, die größer als d und 10n ist.
Sie wählt k Zahlen r1 , ... , rk zwischen 1 und m-1 zufällig,
und nennt Bob die Zahlen m und r1 , ... , rk . - Alice berechnet FP( TA , r1 ) , ... , FP( TA , rk ).
(Schlauerweise ändert sie dazu den Algorithmus FP(T,r) so ab, dass sie mit einem Durchlauf durch den Text TA alle k Resultate berechnet.) - Bob berechnet FP( TB , r1 ) , ... , FP( TB , rk ).
- Alice übermittelt Bob ihre k Resultate.
- Bob vergleicht mit seinen k Werten.
Wenn es Unterschiede gibt, sagt er „ungleich“, und STOP.
Wenn alle Werte gleich sind, sagt er „kein Unterschied zu sehen“, und STOP.
Wenn man den „Fingerprinting-Satz“ benutzt und genauso wie oben argumentiert, nur etwas allgemeiner, erkennt man, dass man folgendes Verhalten garantieren kann:
- Wenn Alice und Bob denselben Text haben, ist das Ergebnis immer „kein Unterschied zu sehen“.
- Wenn Alice und Bob verschiedene Texte haben, ist die Wahrscheinlichkeit, dass sie das (unerwünschte) Resultat „kein Unterschied zu sehen“ bekommen, höchstens
Mit einer passenden Wahl von k können die beiden die Irrtumswahrscheinlichkeit so winzig einstellen, wie sie möchten.

- Wenn m ≈ 10n ist, und n genau l Dezimalziffern hat,
muss Alice nicht mehr als (l+1) · (2+2k) Ziffern übermitteln.
(Es ist erstaunlich, wie gutmütig diese Formel auf eine Vergrößerung der Datenmenge reagiert: Wenn wir einen 10-mal so langen Text zu vergleichen haben, vergrößert sich die Anzahl der zu schickenden Ziffern nur um 2k.)
Fazit:
- Wenn man beim Textvergleich absolute Sicherheit haben will, kann man ein Verfahren zur Datenkompression benutzen, spart aber bei gewöhnlichen Texten nicht mehr als einen Faktor 5 ein.
- Wenn man damit leben kann, dass es eine kleine Wahrscheinlichkeit dafür gibt, dass man verschiedene Texte irrtümlicherweise für gleich hält, dann kann man ein Fingerabdruck-Verfahren benutzen. Dieses verkürzt die zu übermittelnden Botschaften dramatisch.
- Die Irrtumswahrscheinlichkeit ist höchstens (n/m)k bei der Benutzung von k Fingerabdrücken. Man muss dann (2+2k) Zahlen übermitteln, die höchstens so groß wie m sind.
- Die Verwendung von Zufall in Algorithmen und Kommunikationsprotokollen kann zu wesentlichen Einsparungen führen, wenn man bereit ist, in Kauf zu nehmen, dass eventuell ein falsches Ergebnis auftritt — mit einer kleinen Wahrscheinlichkeit.
- Algorithmen oder Protokolle, die manche Entscheidungen oder Auswahlen zufällig treffen, heißen „randomisiert“. (Von englisch „at random“ = zufällig).
(Fast) die Wahrheit:
Dass Alice und Bob einfach nur Freunde sind, war natürlich gelogen. In Wirklichkeit handelt es sich bei Alice um eine Industriespionin im Land A, bei Bob um ihren Kontaktmann im Land B. Die beiden wollen das Lexikon für ein Chiffrierverfahren benutzen, um Nachrichten abhörsicher zu übermitteln. Dabei ist es von äußerster Wichtigkeit, dass beide Texte Wort für Wort übereinstimmen. Das Übermitteln per email ist zu riskant: jemand könnte mithören. Mit einer Irrtumswahrscheinlichkeit von 0,0125 Prozent können die beiden gut leben, angesichts dessen, was beim Spionieren sonst noch alles schief gehen kann ...Andere Anwendungen:
Das Fingerprinting-Verfahren zum Textvergleich kann man immer anwenden, wenn Rechenzeit zum Durcharbeiten der Texte vorhanden, aber Kommunikation teuer oder unsicher ist. Man könnte an den Abgleich der Inhalte von Kopien von Datenbanken nach einer Reihe von Updates denken oder an die regelmäßige Überprüfung, ob die Daten in einem Computer in einer Raumsonde nach Änderungen noch (wie vorgesehen) exakt mit denen des Zwillingscomputers auf der Erde übereinstimmen. Auch zur Textsuche kann man das Fingerprint-Prinzip benutzen; dies liefert ein ganz anderes Verfahren als das im 30. Algorithmus der Woche (Boyer-Moore-Horspool-Algorithmus).
- Prof. Dr. Martin Dietzfelbinger
(Grafik unter Mitwirkung von J. D.)

