Autor
Sigrid Knust, Universität Osnabrück
Die neu gegründete Tischtennisabteilung des TV Schmetterhausen möchte in der kommenden Saison in einer Liga am Punktspielbetrieb teilnehmen und eine Mannschaft mit 6 Spielern melden. Die Mannschaft muss nach Spielstärke aufgestellt sein, d.h. der beste Spieler spielt an Position 1, der zweitbeste an Position 2, usw. Um die Spieler nach Spielstärke ordnen zu können, beschließt der Abteilungsleiter Anton Leiter, ein Turnier durchzuführen. Die 6 ausgewählten Spieler sollen in den nächsten Wochen nach dem System ''jeder gegen jeden'' gegeneinander spielen, danach soll die Mannschaft gemäß der dort ermittelten Rangfolge aufgestellt werden. An jedem Trainingsabend soll jeder Spieler genau ein Spiel austragen.
Die erste Frage, die sich Anton in diesem Zusammenhang stellt, ist die Frage, wie viele Abende für das Turnier benötigt werden. Jeder der 6 Spieler muss genau einmal gegen jeden der 5 anderen Spieler antreten, d.h. es sind insgesamt 6 · 5 / 2 = 15 Spiele zu absolvieren (durch 2 muss geteilt werden, da das Spiel i gegen j sowohl für Spieler i als auch für Spieler j gezählt wird). Anton rechnet: Wenn jeder der 6 Spieler an jedem Trainingsabend genau ein Spiel austrägt, finden 3 Spiele pro Abend statt, d.h. es werden somit 15 / 3 = 5 Abende benötigt, um alle Spiele durchzuführen.
Hochmotiviert legen die Spieler der Abteilung los, wobei sich an jedem Abend jeder Spieler einen Gegner sucht, gegen den er noch nicht gespielt hat. Nach drei Abenden sind folgende Begegnungen absolviert:
| 1. Abend | 2. Abend | 3. Abend |
| 1-2 | 1-3 | 1-4 |
| 3-5 | 2-6 | 2-5 |
| 4-6 | 4-5 | 3-6 |
Es ist leicht zu überprüfen, dass die restlichen 6 Spielpaarungen 1-5, 1-6, 5-6, 2-3, 2-4, 3-4 nicht an zwei weiteren Abenden beendet werden können (wenn 1-5 spielt, kann dazu weder das Spiel 1-6 noch das Spiel 5-6 parallel ausgetragen werden, da jeder Spieler nur einmal pro Abend spielen soll). Das Turnier lässt sich nur mit drei weiteren Abenden beenden:
| 4. Abend | 5. Abend | 6. Abend |
| 1-5 | 1-6 | 5-6 |
| 2-3 | 2-4 | 3-4 |
Für das Turnier benötigt die Abteilung somit einen Abend länger als ursprünglich geplant, außerdem müssen an jedem der letzten Abende zwei Spieler aussetzen. Da man hinterher bekanntlich immer schlauer ist, fragt sich Anton, ob das so sein muss oder ob die Abteilung mit einem anderen Spielplan ihr Turnier auch schon nach 5 Abenden hätte beenden können. Bei der abendlichen Sportschau stellt Anton fest, dass die Fußballbundesliga eigentlich ein ähnliches Problem hat. Dort müssen 18 Mannschaften in einer Hin- und Rückserie jeweils genau einmal gegen jede andere Mannschaft spielen, wobei in jeder Runde (Wochenende) jede Mannschaft genau ein Spiel austrägt. Anton denkt zurück und erinnert sich, dass in den letzten Jahren jede Saison in 2 · 17 = 34 Wochen beendet werden konnte und nie eine Mannschaft in einer Runde aussetzen musste. Er fragt sich, ob es immer einen solchen Spielplan gibt oder ob evtl. die Zahl 18 günstiger als die Zahl 6 ist.
Verlassen wir jetzt einmal Anton, den TV Schmetterhausen sowie die Fußballbundesliga und betrachten unser Problem etwas allgemeiner: Gegeben sind eine gerade Anzahl n von Mannschaften (oder Spielern) und n-1 Runden (Spieltage). Gesucht ist ein Spielplan, so dass jede Mannschaft genau einmal gegen jede andere spielt und jede Mannschaft in jeder Runde genau ein Spiel austrägt. Die Frage ist, ob es für jede gerade Zahl n einen solchen Spielplan gibt und wenn ja, wie man ihn konstruieren kann. Die Antwort ist, dass für jedes gerade n eine Lösung existiert (also sowohl für n=18 als auch für n=6, aber auch für n=100 oder n=1024). Im Folgenden werden wir einen Algorithmus angeben, der für jedes n einen solchen Spielplan berechnet.
Um den Algorithmus anschaulich beschreiben zu können, modellieren wir unser Problem zunächst mit Hilfe von so genannten Graphen, die generell in der Informatik eine wichtige Rolle spielen. Ein Graph besteht aus einer Menge von Knoten und Kanten, wobei eine Kante jeweils zwei Knoten miteinander verbindet. Auf diese Weise lassen sich z.B. Straßennetzwerke (vgl. den 23. Algorithmus der Woche) modellieren, bei denen Straßen den Kanten und Kreuzungen den Knoten entsprechen.
Bei unserem Turnier- oder Sportligaplanungsproblem führen wir für jede
Mannschaft einen Knoten ein, die Spiele entsprechen den Kanten. Für n=6
Mannschaften erhält man folgenden Graphen:

Einen solchen Graphen nennt man auch vollständig, da jeder Knoten mit jedem anderen Knoten durch eine Kante verbunden ist (zur Erinnerung: jede Mannschaft soll gegen jede andere spielen). Um einen Spielplan zu erhalten, färben wir nun die Kanten mit den Farben 1,2,...,n-1, wobei jede Farbe eine Runde repräsentiert. Eine solche Färbung wollen wir zulässig nennen, wenn sie einem zulässigen Spielplan entspricht. Dazu müssen alle Kanten, die in den gleichen Knoten hineinführen, unterschiedlich gefärbt sein (sonst ist die Bedingung verletzt, dass jede Mannschaft in jeder Runde nur einmal spielt).
Für unseren Graphen mit n=6 Knoten ist z.B. die unten abgebildete Kantenfärbung mit n-1=5 Farben zulässig. Ein zugehöriger Spielplan ist neben dem Graphen dargestellt, wobei die Farbe ''rot'' die erste Runde repräsentiert, die Farbe ''blau'' die zweite Runde, usw.
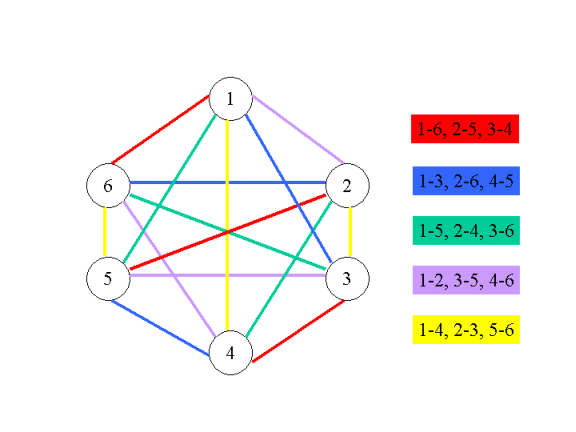
Es bleibt die Frage, wie man für jede gerade Zahl n eine zulässige Kantenfärbung für den vollständigen Graphen mit n Knoten bestimmen kann. Betrachten wir in dem Beispiel einmal den Graphen, der entsteht, wenn wir Knoten 6 und alle 5 Kanten, die in ihn hineinführen, entfernen. Es ergibt sich ein 5-Eck, bei dem die 5 Kanten auf dem Rand (1-2, 2-3, 3-4, 4-5, 5-1) alle unterschiedlich gefärbt sind. Zeichnen wir das 5-Eck wie unten als regelmäßiges 5-Eck (d.h. die Innenwinkel an allen 5 Ecken sind gleich), fällt auf, dass jede Kante im Inneren des 5-Ecks die gleiche Farbe wie die zugehörige parallele Kante auf dem Rand hat. Sind bei einer Kantenfärbung immer nur parallele Kanten (die ja keinen Knoten gemeinsam haben) mit der gleichen Farbe gefärbt, ist unsere obige Bedingung erfüllt, dass Kanten, die in den gleichen Knoten hineinführen, stets unterschiedlich gefärbt sind. Bei unserem Beispiel sehen wir weiterhin, dass bei jedem der 5 Knoten 4 Farben verbraucht sind und jeweils eine andere Farbe unbenutzt ist (die jeweils für die Kante zum Knoten 6 genutzt werden kann).
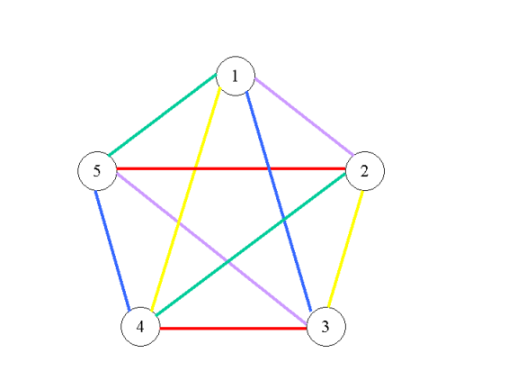
Diese Beobachtungen lassen sich zu einem Konstruktionsverfahren für eine Kantenfärbung für jeden Graphen mit einer geraden Anzahl n von Knoten umsetzen. Im Folgenden stellen wir einen Algorithmus vor, der in n-1 Schritten jeweils eine Menge von parallelen Kanten mit einer anderen Farbe färbt (vgl. auch die Abbildung unter dem Algorithmus). Man kann zeigen, dass dieser Algorithmus für jede gerade Zahl n funktioniert und eine zulässige Kantenfärbung liefert. Die so entstandene Färbung wird auch kanonische 1-Faktorisierung genannt (die Kantenmengen einer Farbe bilden jeweils einen so genannten 1-Faktor im Graphen).
Algorithmus Kantenfärbung (geometrische Version)
- Bilde aus den Knoten 1,2,...,n-1 ein regelmäßiges (n-1)-Eck und platziere den Knoten n links oben neben dem (n-1)-Eck.
- Verbinde den Knoten n mit der ''Spitze'' des (n-1)-Ecks.
- Verbinde die übrigen Knoten jeweils mit dem gegenüberliegenden Knoten auf der gleichen Höhe im (n-1)-Eck.
- Die eingefügten n/2 Kanten werden mit der ersten Farbe gefärbt (im Beispiel werden die Kanten 6-1, 5-2, 4-3 rot gefärbt).
- Verschiebe die Knoten 1,...,n-1 des (n-1)-Ecks gegen den Uhrzeigersinn zyklisch um eine Position weiter (d.h. Knoten 2 geht auf den Platz von Knoten 1, Knoten 3 ersetzt den alten Knoten 2, ..., Knoten n-1 ersetzt den alten Knoten n-2 und Knoten 1 ersetzt den alten Knoten n-1). Der Knoten n behält seinen Platz neben dem (n-1)-Eck und die in den Schritten 2 und 3 eingefügten Kanten behalten ihre Position im (n-1)-Eck.
- Die neu resultierenden n/2 Kanten werden mit der zweiten Farbe gefärbt (im Beispiel werden die Kanten 6-2, 1-3, 5-4 blau gefärbt).
- Die Schritte 5 und 6 des Verfahrens werden für die übrigen Farben 3,...,n-1 wiederholt.
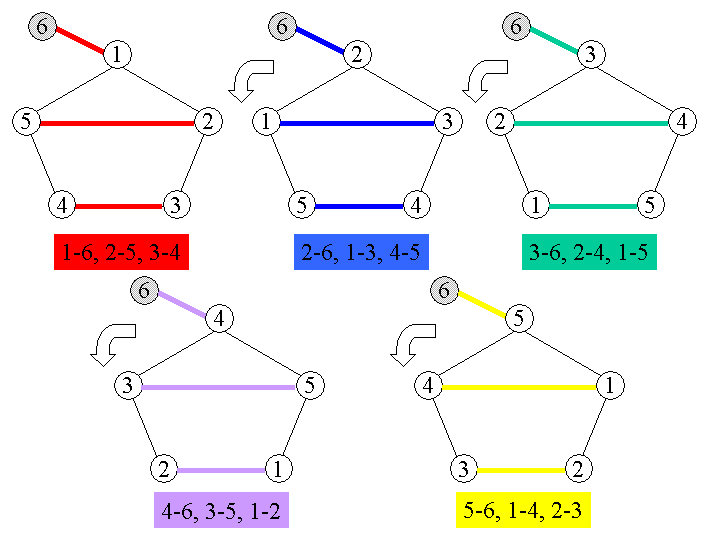
Um den obigen Algorithmus in ein Computerprogramm umzusetzen, wäre es relativ aufwändig, (n-1)-Ecke zu speichern und in jedem Schritt Knoten zyklisch zu verschieben. Wenn man die ganzzahlige Division mit Rest beherrscht (Modulo-Rechnung, vgl. den 18. Algorithmus der Woche), lässt sich der Algorithmus viel einfacher in 3 Schritten aufschreiben:
Algorithmus Kantenfärbung (zahlentheoretische Version)
In diesem Algorithmus bedeutet die Schreibweise a mod b, dass man die Zahl a ganzzahlig durch die Zahl b teilt und den Rest nimmt, der dabei entsteht. So ist z.B.
- 14 mod 4 = 2 da 14 = 3 · 4 + 2,
- 9 mod 3 = 0 da 9 = 3 · 3 + 0, und
- -1 mod 5 = 4 da -1 = (-1) · 5 + 4.
Für unser Beispiel erhält man in Schritt 3 für i=1 die Kanten
- [(1+1) mod 5, (1-1) mod 5] = [2,5] für k=1, und
- [(1+2) mod 5, (1-2) mod 5] = [3,4] für k=2.
Wir kommen nun noch einmal zur Fußballbundesliga zurück. Im Gegensatz zu unserem Tischtennis-Turnier finden die Spiele nicht alle am gleichen Ort statt, sondern in den Stadien der jeweiligen Mannschaften. Wird das Spiel zwischen den Mannschaften i und j in der Hinserie im Stadion der Mannschaft i ausgetragen, so wird in der Rückserie bei Mannschaft j gespielt. Ein Spielplan besteht somit nicht nur aus den Spielpaarungen pro Runde (wer spielt gegen wen?), sondern es muss zusätzlich für jede Spielpaarung noch das Heimrecht festgelegt werden (wo findet das Spiel statt?).
Aus verschiedenen Gründen (Fairness, Attraktivität für Zuschauer) sollten sich Heim- und Auswärtsspiele für jede Mannschaft möglichst abwechseln. Spielt eine Mannschaft zweimal hintereinander zu Hause oder zweimal hintereinander auswärts, so sagt man auch, dass die Mannschaft ein Break hat (die abwechselnde Folge von H- bzw. A-Spielen ist unterbrochen). Sind Breaks unerwünscht, wäre natürlich ein Spielplan am besten, bei dem keine Mannschaft ein Break hat. Betrachtet man jedoch den Spielplan der Fußballbundesliga etwas genauer, erkennt man, dass dort in jeder Saison Breaks auftreten. Wieder können wir uns fragen, ob das so sein muss oder ob es bessere Pläne (ohne Breaks) gibt.
Man kann sich relativ leicht überlegen, dass es bei unseren Voraussetzungen keinen Spielplan ohne Breaks geben kann. Hätten alle Mannschaften kein Break, so müsste jede Mannschaft die Spielfolge HAHA...H oder AHAH...A haben. Zwei Mannschaften mit dem gleichen Spielfolgemuster (z.B. HAHA...H) können jedoch nie gegeneinander spielen (da sie beide immer entweder zu Hause oder auswärts spielen). Aus diesem Grund können höchstens zwei Mannschaften kein Break haben (eine Mannschaft mit der Spielfolge HAHA...H, eine andere mit AHAH...A). Daraus folgt, dass die übrigen n-2 Mannschaften mindestens ein Break haben müssen, jeder Spielplan für eine Halbserie also mindestens n-2 Breaks hat.
Man kann zeigen, dass es Spielpläne mit genau n-2 Breaks gibt und sie sich mit einer Erweiterung des obigen Algorithmus berechnen lassen. Als einzige Erweiterung muss man dabei in den Schritten 2 und 3 zusätzlich das Heimrecht wie folgt festlegen:
- Das Spiel [i,n] ist ein Heimspiel für Mannschaft i, wenn i gerade ist; sonst ist es ein Heimspiel für n.
- Das Spiel [(i+k) mod (n-1), (i-k) mod (n-1)] ist ein Heimspiel für Mannschaft (i+k) mod (n-1), wenn k ungerade ist; sonst ist es ein Heimspiel für (i-k) mod (n-1).


Zum Abschluss kommen wir noch einmal zur Fußballbundesliga zurück. Da dort eine Hin- und eine Rückserie gespielt werden, treten natürlich mehr Breaks auf. Beim System der deutschen Bundesliga finden die Spiele der Rückserie in der gleichen Reihenfolge wie die Spiele in der Hinserie statt (mit getauschtem Heimrecht). Für dieses System lässt sich zeigen, dass mindestens 3n-6 Breaks auftreten. Ein Plan mit 3n-6 Breaks (jeweils n-2 in den beiden Halbserien und n-2 beim Übergang von der Hin- zur Rückserie) lässt sich mit der obigen Methode konstruieren. Für kleine Werte von n könnt ihr das einmal selbst ausprobieren.
In der Praxis ist die Planung einer Sportliga jedoch meist viel schwieriger, da zusätzliche Nebenbedingungen berücksichtigt werden müssen. So ist z.B. zu beachten, dass zwei Mannschaften, die das gleiche Stadion für Heimspiele nutzen, nicht gleichzeitig in einer Runde zu Hause spielen. Außerdem sollten aufgrund von Bahn- oder Polizeikapazitäten nicht zu viele Heimspiele in einer Region (nahe beieinander liegende Orte) stattfinden. Des weiteren kann es passieren, dass in manchen Runden ein Stadion nicht zur Verfügung steht, da dort bereits eine andere Veranstaltung (Konzert, Messe oder eine andere Sportveranstaltung) geplant ist. In diesem Fall muss die entsprechende Mannschaft in dieser Runde auswärts spielen. Die Medien und Zuschauer möchten eine Saison erleben, die lange spannend bleibt (d.h. Spitzenspiele sollten eher zum Ende der Saison stattfinden) und attraktive Spiele sollten möglichst gleichmäßig über die Saison verteilt sein.
In den meisten Ligen werden Spielpläne per Hand konstruiert (so auch beim DFB). Ein Planer generiert mit der obigen Methode einen Spielplan für seine Ligagröße, wobei er zunächst die Zahlen 1,...,n als Platzhalter für die Mannschaften einsetzt. In einem zweiten Schritt wird dann jeder Zahl eine konkrete Mannschaft zugeordnet (z.B. 1=Werder Bremen, 2=Hamburger SV, 3=Bayern München, usw.). Dabei wird versucht, möglichst viele zusätzliche Nebenbedingungen zu erfüllen (z.B. dass zwei Mannschaften, die das gleiche Stadion nutzen, Platzhaltern zugeordnet werden, die nie gleichzeitig ein Heimspiel haben).
Wir wollen uns einmal überlegen, wie viele verschiedene solcher Zuordnungen es bei einer Liga mit n=18 Mannschaften gibt. Zunächst hat man für die erste Zahl 18 Mannschaften zur Auswahl, danach für die zweite Zahl nur noch 17 Möglichkeiten (da eine Mannschaft bereits festgelegt ist), dann 16 Möglichkeiten für die dritte Zahl, usw. Insgesamt ergeben sich 18! = 18 · 17 · 16 · ... · 2 · 1 = 6,4 · 10 15 Möglichkeiten (allgemein n Fakultät). Unter der Voraussetzung, dass ein Computer eine Milliarde Lösungen pro Sekunde generieren könnte, müssten wir 74 Tage rechnen, um alle Möglichkeiten auszuprobieren. Diese riesige Zahl zeigt, dass ein menschlicher Planer selbst mit Computerunterstützung nur eine kleine Anzahl von möglichen Plänen ausprobieren kann. Ein weiterer Nachteil der gerade beschriebenen Methode besteht darin, dass nur ein möglicher Spielplan als Grundlage für die Zuordnung genommen wird. Es gibt eine Vielzahl von anderen Plänen, die nicht durch die obige Methode generiert werden können. Das bedeutet, dass mit dieser Methode evtl. gute Pläne (d.h. Pläne, die möglichst viele Nebenbedingungen erfüllen) nicht gefunden werden. Aus diesem Grund beschäftigt sich aktuelle Forschung im Bereich Sportligaplanung mit der Entwicklung von neuen Verfahren, mit denen möglichst gute Spielpläne in akzeptabler Rechenzeit berechnet werden können.
- Wikipedia: Graphen
- Mathworld: Graphen
- Mathworld: Kantenfärbung
- Sports scheduling
- Literatur Sports scheduling
- Implementierung des Algorithmus in PHP von Andy Theiler
- Visualisierung von Algorithmen zur Sportligaplanung

