Autor
Leif Kobbelt, RWTH Aachen
Dominik Sibbing, RWTH Aachen
Hast Du schon einmal versucht, ein Bild zu zeichnen? Dabei kann man feststellen, dass sich eine Zeichnung im Prinzip aus einer Ansammlung und Kombination von vielen kleinen geometrischen Grundbausteinen zusammensetzt. Diese Grundbausteine können z.B. Linien oder auch Kreise sein.
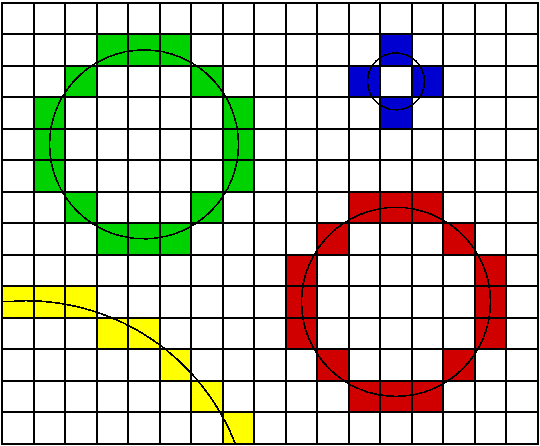
Ein Computer zeichnet diese Grundbausteine, indem er Punkte, die sogenannten Pixel (Abk. für "picture element") auf dem Monitor farbig sichtbar macht. Dies ist vergleichbar mit dem Ausmalen eines Kästchens auf karriertem Papier. Schaltet man viele nebenenanderliegende Pixel an, so ensteht z.B. eine Linie oder ein Kreis. Zusammen mit weiteren Linien und anderen geometrischen Bausteinen entsteht auf diese Weise ein Bild (Abb. 1). Auf dem Monitor können einzelne Pixel nur bei sehr genauem Hinsehen erkannt werden, da heutige Monitore eine sehr hohe Auflösung von oft mehr als 1280 x 1024 Pixeln haben. Im Vergleich dazu hat ein normales Fernsehbild nur eine Auflösung von 720 x 576 Pixeln.
|
| Abb. 1: Zeichnung mit Kreisen |
In vielen Anwendungen wie z.B. 3D Computerspielen stellt sich die Frage, wie solche geometrischen Grundbausteine möglichst schnell, d.h. mit möglichst wenigen und einfachen Rechenoperationen, gezeichnet werden können. Wir wollen Dir dies am Beispiel von Kreisen verdeutlichen.
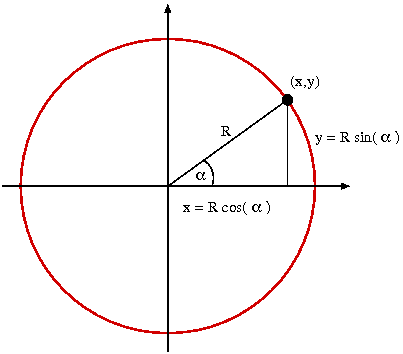
Um einen Kreis zu zeichnen, wird einem wohl zuerst der Zirkel als ideales Hilfsmittel einfallen, der auf dem einfachen Prinzip beruht, den Abstand der Zirkelspitze zum Mittelpunkt konstant zu lassen, während sie sich um 360° um den Mittelpunkt herumdreht. Möchten wir die Methode des Zirkels nachahmen, so müssen wir berechnen können, wo sich die Zirkelspitze zu jedem Zeitpunkt aufhält. Weiß man den Radius des Kreises R und den Winkel alpha, den die x-Achse und die Verbindungslinie der Zirkelspitze einschließen, so lässt sich die Position der Zirkelspitze über die Sinus und Cosinus Funktion wie folgt bestimmen:

wobei R der Radius des Kreises ist (Abb 2).
|
| Abb. 2: Parametrisierung des Kreises |
Nehmen wir an, wir hätten einen Befehl "plot(x,y)", der ein Pixel auf dem Monitor anschalten kann. Ein Kreis entsteht nun, indem mit Hilfe der oben genannten Formel eine Menge von Pixel auf dem Monitor angeschaltet werden. Hierzu starten wir einen ersten Versuch:
Naiver_Algorithmus
Wie man sieht, läuft der Winkel von 0 bis 360°, was wie beim Zeichnen mit dem Zirkel zu einem vollständigen Kreis führt.
Wie aber wählen wir die Anzahl N der Punkte?
Auf der einen Seite wollen wir möglichst wenige Punkte berechnen, da bei der Betrachtung von zu vielen Punkten unter Umständen immer wieder dieselben Pixel gesetzt werden, was unnötig Rechenzeit in Anspruch nehmen würde. Auf der anderen Seite dürfen aber auch nicht zu wenig Punkte betrachtet werden, weil sonst Lücken im Kreis entstehen könnten. Bei einer Pixelbreite von 1 Längeneinheit lässt sich mit Hilfe der Formel für den Kreisumfang

ungefähr abschätzen, dass man 7R Pixel benötigt, um den Kreis zu zeichnen.
Obgleich der Algorithmus korrekt funktioniert, erfordern die vielen Multiplikationen, Additionen und auch die Auswertung der Sinus und Cosinus Ausdrücke einen hohen Rechenaufwand, was bei Bildern mit sehr vielen Kreisen zu langen Wartezeiten vor dem PC führt.
Die Frage ist also: Lässt sich Rechenzeit sparen?
Als erstes fällt sicherlich die Symmetrie des Kreises auf. Zeichnet man nur den oberen Halbkreis, so lässt sich durch Spiegelung der Punkte an der x-Achse leicht der andere Halbkreis ergänzen. Diese Spiegelung ist besonders einfach, weil nur das Vorzeichen der y-Koordinate geändert werden muss.
Dazu kommt, dass das Zeichnen des oberen Halbkreises schneller geht, wenn man sich den Satz von Pythagoras zu Nutze macht. Mit ihm lässt sich die Höhe y in Abhängigkeit von x sofort ausrechnen (siehe auch Abb. 2):
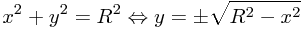
Diese Überlegungen führen zu einem verbesserten Algorithmus, der mit weniger Berechnungen auskommt
Verbesserter_Naiver_Algorithmus
Die innere Schleife über y sorgt hier dafür, dass keine Lücken im Kreis entstehen. Man beachte nämlich, dass an einer bestimmten Stelle auf der x-Achse auch mehrere Punkte übereinander liegen können, was besonders an der rechten und linken Seite des Kreises auftritt.
Wie man erkennt, wird die x-Koordinate nur aufgezählt und nicht mehr berechnet. Für die Berechnung der y-Koordinate muss lediglich eine Wurzel ausgewertet werden, der Sinus ist nicht mehr nötig. Lässt man den ersten Algorithmus gegen den neuen Algorithmus im Computer laufen, so kann man feststellen, dass der neue Algorithmus etwa 7.5 mal scheller ist!
Denkt man nochmal kurz über die Symmetrie nach, so fällt auf, dass die Spiegelung an der y-Achse ebenso einfach ist. Hier muss lediglich die x-Koordinate des berechneten Punktes mit einem "Minus" versehen werden. Nun reicht es schon aus, nur ein Viertel des Kreises zu berechnen.
Können wir das vielleicht noch weiter treiben? Ja! Auch die Spiegelungen an den beiden Diagonalen im Koordinatensystem ist besonders einfach. Hier werden nur die Koordinaten des Punktes (x,y) vertauscht. Aus (x,y) wird also ganz einfach (y,x), wir berechnen nur noch ein Achtel des Kreises, also z.B. den Bereich zwischen 12:00 und 13:30 Uhr, und ergänzen den Rest, wie es in der Abbildung 3 zu sehen ist.

|
| Abb. 3: Symmetrie des Kreises |
Ist also (x,y) bekannt, so sind auch die Punkte (y,x), (-y,x), (x,-y), (-x,-y), (-y,-x), (y,-x) und (-x,y) quasi ohne Rechenaufwand ableitbar. Das verringert den Rechenaufwand fast um den Faktor 8.
Nun wenden wir uns der Berechnung der Punke (x,y) zu, die immer noch recht aufwändig ist. Die Frage ist, kann diese Berechnung auf einfache Multiplikations- bzw. Additionsoperationen reduziert werden? D.h. ist es möglich, auf die Berechnung der Wurzel ganz zu verzichten? Der Bresenham Algorithmus für Kreise liefert hier die positive Antwort!
Die Idee des Verfahrens ist folgende. Man beginnt mit dem Zeichnen des obersten Pixels (0,R). In jedem Schritt des Algorithmus wird die x-Koordinate um eins erhöht. Da im ersten Achtel des Kreises die Steigung zwischen 0 und -1 liegt (Abb. 4), kann die y-Koordinate entweder gleich bleiben, das heißt wir bewegen uns nach "Osten", oder um eins verringert werden, was der Bewegung nach "Süd-Osten" entspricht. Diese Entscheidung wird getroffen, indem man überprüft, ob der Mittelpunkt des neu berechneten Pixels (blauer Punkt in Abb. 4) möglichst nahe am Kreis (rot) liegt.
|
|
| Abb. 4: Bresenham für Kreise |
Das wird solange gemacht, bis der Achtelkreis und damit über Spiegelungen der komplette Kreis berechnet wurde.
Um zu entscheiden, ob das Zentrum des östlichen oder das des südöstlichen Nachbarpixels näher am Kreis liegt, schaut man sich die im Bild grün eingezeichneten Punkte an. Diese Punkte sind immer um eine Einheit nach rechts und eine halbe Längeneinheit nach unten gegenüber der aktuellen Position des blauen Punktes verschoben. Demnach werden sie mit der Position (1,R-1/2) initialisiert.
Die Entscheidung sieht nun wie folgt aus:
Fall 1: Liegt der grüne Punkt innerhalb des Kreises, so bewegen wir uns im nächsten Schritt nur nach Osten.
-> Aus (x,y) wird (x+1,y).
Fall 2: Liegt er außerhalb des Kreises, so bewegen wir uns nach Süd-Osten.
-> Aus (x,y) wird (x+1,y-1)
Aber wie lässt sich feststellen, ob ein Punkt innerhalb oder außerhalb des Kreises liegt?
Ein Punkt (x,y) liegt immer dann innerhalb eines Kreises, wenn der Abstand zwischen dem Punkt und dem Kreismittelpunkt kleiner als der Kreisradius ist. Das ist gleichbedeutend damit, dass die Funktion
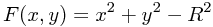
einen Wert <0 liefert. Das Gute ist: dieser Test erfordert keine Wurzelberechnung mehr!
Der Funktionswert des ersten grünen Punktes ist schnell gefunden:

Entscheiden wir uns dafür, von einem Punkt (x,y) nach Osten zu laufen, so ändert sich der Wert der Entscheidungsfunktion F in folgender Weise:

Bei der Entscheidung ein Pixel nach Süd-Osten zu laufen, ergibt sich der neue Wert von F als
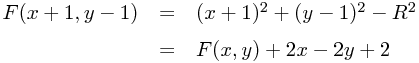
Danach wird das neue Pixel gesetzt und das ganze beginnt von vorne. Diese "inkrementelle" Berechnung ist deutlich effizienter als den Term F(x,y) jedesmal neu auszuwerten.
Die Informationen über die Initialisierung und die Updateschritte würden uns erlauben, eine erste Version des Bresenham Algorithmus für Kreise anzugeben. Etwas unschön erscheint aber noch der Bruch aus der Initialisierung von F. Es wäre wünschenswert, nur mit ganzen Zahlen zu rechnen, weil eine Berechnung auf ganzen Zahlen im Computer einfacher durchgeführt werden kann als auf rationalen Zahlen. Ohne weiter ins Detail zu gehen, liegt diese Tatsache einfach an der Art und Weise wie Zahlen im Computer dargestellt werden.
Würde F bei der Initialisierung eine ganze Zahl sein, so würde dies durch keinen der oben aufgeführten Updates geändert, weil eben auch nur ganze Zahlen addiert werden.
Um auf den Bruch verzichten zu können, fragen wir uns, was es bedeutet, wenn F<0 ist. Aus dem Startwert
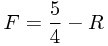
und der Tatsache, dass F nur um ganze Zahlen verändert wird, erkennt man, dass F zu jedem Zeitpunkt gleich K+1/4 für eine ganze Zahl K ist. Damit liegt F in folgender Menge

Wenn F<0 ist, so muss also gelten:
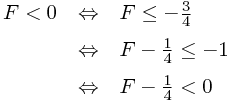
Da F-1/4 eine ganze Zahl ist, kann demnach F auch als F = 1-R initialisiert werden, ohne dass die Entscheidung nach Osten oder Süd-Osten zu gehen falsch getroffen werden kann.
Nun können wir den Bresenham Algorithmus für das Kreisezeichnen angeben:
Bresenham-Algorithmus
Eine letzte Vereinfachung betrifft die beiden Updateschritte. Schreibt man beide Updates etwas anders hin, so fällt schnell eine weitere Verbesserung des Algorithmus auf, die die Reihenfolge der Schritte betrifft. Das erste Update lässt sich auch schreiben als
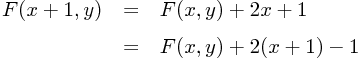
während das zweite Update auch darstellbar ist als:
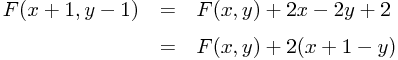
In beiden Ausdrücken kommt der Term (x+1) vor, so dass wir die Inkremente für F sogar noch leicht vereinfachen können, wenn wir x vor dem Update der Entscheidungsfunktion erhöhen.
Der Algorithmus wird so nocheinmal einfacher und kann in der folgenden Form geschrieben werden.
Verbesserter_Bresenham-Algorithmus
Mit diesem sehr kurzen Algorithmus ist das Zeichnen von Kreisen ein Leichtes: Lässt man die Algorithmen (Quellcodes in C) in einem kleinen Beispielprogramm zur Zeitmessung laufen, so zeigt sich, dass mit diesem Ansatz das Zeichnen von Kreisen ungefähr 14 mal so schnell geht, wie mit dem ersten vorgeschlagenem Verfahren. Zudem werden alle Operationen auf ganzen Zahlen ausgeführt, was der Genauigkeit zu Gute kommt.
Ähnliche Algorithmen existieren auch für die anderen geometrischen Grundbausteine, wie z.B. die Linie oder das Dreieck. Diese sind oft auf einer sehr niedrigen Ebene in Grafiktreibern implementiert, so dass Bilder sehr schnell berechnet werden können, was von enormer Wichtigkeit für viele Anwendungen wie z.B. die 3D Computerspiele ist. In dieser speziellen Anwendung sollen oft mehr als 40 Bilder pro Sekunde erzeugt werden, die ihrerseits wiederum aus sehr vielen dieser geometrischen Grundbausteinen bestehen können.
Abschließend lässt sich sagen, dass es für die Lösung eines Problems, wie z.B. das Zeichnen von Kreisen, in der Informatik oft verschiedene Wege gibt. Am Anfang muss die Natur des Problemes verstanden werden. Ist einmal eine erste Lösung gefunden und dadurch das Problem besser verstanden, kann versucht werden, diese Lösung zu verbessern. Zusätzliches Wissen wie in diesem Fall die Symmetrie des Kreises oder Sätze der Mathematik helfen bei diesem Prozess. Informationen über die Computerarchitektur wie z.B. die Tatsache, dass die Berechnung einfacher Inkremente schneller ausgeführt werden kann als das Auswerten komplizierter Ausdrücke, führen schließlich zu Algorithmen die äußerst effizient arbeiten.

