Autor
Stefan Näher, Universität Trier
Das Problem des Handlungsreisenden
Das Travelling Salesman Problem (TSP) ist eines der bekanntesten und meist untersuchten Optimierungsprobleme. Es stellt sich wie folgt. Ein Handlungsreisender soll in einer Rundreise (auch Tour genannt) n vorgegebene Städte besuchen. Er startet dazu in einer dieser Städte, besucht nacheinander die restlichen Städte, und kehrt schließlich zu seinem Ausgangspunkt zurück. Das eigentliche Optimierungsproblem besteht darin, die Rundreise so zu planen, dass ihre Gesamtlänge minimiert wird. Die Entfernungen zwischen allen Paaren von Städten sind hierzu (z.B. in Form einer Tabelle) gegeben. Neben den tatsächlichen geometrischen Abständen kann es sich dabei auch um Reisezeiten oder um andere Kosten (z.B. für Treibstoff) handeln. Ziel ist also, die Rundreise so zu planen, dass der Gesamtreiseweg bzw. die Reisezeit oder aber die insgesamt anfallenden Kosten minimiert werden.

Das liegt daran, dass das TSP-Problem zu einer Klasse von sehr schwierigen Problemen gehört, den sogenannten NP-vollständigen Problemen. Für diese Probleme ist kein effizienter Algorithmus bekannt. Es wird vielmehr angenommen, dass jeder deterministische Algorithmus zur exakten Lösung dieser Probleme mindestens exponentiell viele Rechenschritte ausführen muss. Bis heute existiert jedoch kein mathematischer Beweis für diese Vermutung. Für spezielle Varianten von TSP und zur Berechnung von Näherungslösungen, die auch Rundreisen erlauben, die etwas teurer sind als die optimale Tour, sind allerdings sehr schnelle Algorithmen bekannt.
Das TSP-Problem tritt in der Praxis in vielen Anwendungen als Teilproblem auf. Hierzu gehören z.B. Optimierungsprobleme in der Verkehrsplanung und Logistik oder beim Entwurf integrierter Schaltungen und Mikrochips. Man kann auch andere Probleme aus der Klasse der NP-vollständigen Probleme auf TSP zurückführen. Wir werden zunächst eine sehr einfache Strategie zur exakten Lösung von TSP untersuchen, die sogenannte brute-force Technik (wir nennen sie auch Holzhammermethode), und zeigen wie katastrophal langsam ein Algorithmus mit exponentieller Laufzeit sein kann.
Die Holzhammer-Methode
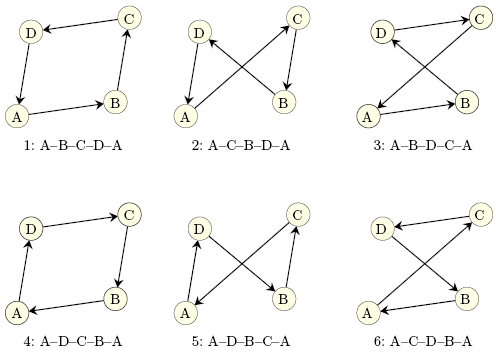
Die “Holzhammer-Methode”, die auch brute-force oder naive Methode genannt wird, ist der einfachste Algorithmus zur exakten Lösung von TSP. Er betrachtet nacheinaner alle möglichen Rundreisen, berechnet für jede die Gesamtlänge und ermittelt durch Vergleich der so erhaltenen Werte die kürzeste Tour. Leider wächst aber die Zahl aller möglichen Rundreisen mit steigender Zahl n der gegebenen Städte sehr schnell. Man kann sich leicht überlegen, dass es insgesamt (n − 1)! = 2 · 3 · 4 · . . . · (n − 1) verschiedene Möglichkeiten gibt, n Orte mit einer Rundreise zu besuchen: jede Rundreise muss in einer Stadt (z.B. der ersten) beginnen, die restlichen n − 1 Städte in irgendeiner Reihenfolge besuchen, und dann wieder zur ersten Stadt zurückkehren. Es gibt aber genau (n − 1)! Möglichkeiten, die restlichen (n − 1) Städte nacheinander aufzuzählen (man spricht auch von der Zahl der Permutationen). Abbildung 1 zeigt die 6 = (4 − 1)! möglichen Rundreisen für 4 Städte A,B,C,D.
Städte |
mögliche Rundreisen |
Laufzeit |
3 |
1 |
1 msec |
4 |
3 |
3 msec |
5 |
12 |
6 msec |
6 |
60 |
60 msec |
7 |
360 |
360 msec |
8 |
2.520 |
2,5 sec |
9 |
20.160 |
20 sec |
10 |
181.440 |
3 min |
11 |
1.814.400 |
0,5 Stunden |
12 |
19.958.400 |
5,5 Stunden |
13 |
239.500.800 |
2,8 Tage |
14 |
3.113.510.400 |
36 Tage |
15 |
43.589.145.600 |
1,3 Jahre |
16 |
653.837.184.000 |
20 Jahre |
Bei den unteren drei Touren handelt es sich, wie man leicht sieht, um Umkehrungen der oberen drei Touren, so dass man eigentlich nur für die Hälfte der Rundreisen die Gesamtlängen ausrechnen muss. Bei n Städten muss der Algorithmus also 1/2 · (n−1)! Rundreisen betrachten. Es gibt übrigens auch Varianten von TSP ohne diese Symmetrie-Eigenschaft. Dann muss man tatsächlich alle Touren untersuchen.
Tabelle 1 zeigt, wie gewaltig schnell die Zahl der Rundreisen mit steigendem n wächst. Die letzte Spalte gibt eine Abschätzung für die Laufzeit eines Programms an, das TSP mithilfe der Holzhammermethode zu lösen versucht. Dabei wird angenommen, dass die Bearbeitung einer einzigen Rundreise etwa eine Millisekunde Zeit benötigt. Die letzte Zeile der Tabelle zeigt, dass ein solches Programm für die Lösung eines TSP-Problems mit nur 16 Städten mehr als eine halbe Billionen Rundreisen betrachten muss und so über 20 Jahre Rechenzeit benötigt.
Laufzeiten im Minutenbereich sind nur für Probleme mit maximal 10 Städten möglich. Im Algorithmus der Woche 15 tritt ein ähnliches Problem mit einer extrem schnell wachsenden Anzahl von Möglichkeiten auf.
Dynamisches Programmieren
Eine Technik, die in der Informatik und insbesondere beim Entwurf von Algorithmen sehr häufig eingesetzt wird, ist die Rekursion. Dabei versucht man, die Lösung eines Problems auf kleinere Probleme der gleichen Art zurückzuführen, siehe auch Algorithmus der Woche 3. Das sogenannte Dynamischen Programmieren ist eine spezielle Variante dieser Technik, bei der man Zwischenresultate von rekursiv definierten Teilproblemen in einer Tabelle verwaltet.
Wir nehmen an, dass die n Städte mit den Zahlen von 1 bis n durchnummeriert sind, d.h.
wir können die Menge der Städte als Menge S = { 1, 2, . . . , n } schreiben, und dass die
Entfernungen oder Kosten in einer Tabelle DIST gegeben sind, d.h. DIST [i, j] bezeichnet
die Entfernung von Stadt i nach Stadt j. Da eine Rundreise in jeder beliebigen Stadt beginnen
und enden kann, nehmen wir zur Vereinfachung an, dass jede Rundreise in der Stadt 1 beginnt,
dann zu einer Stadt i  { 2, . . . , n } führt, dann alle restlichen Städte { 2, . . . , i-1, i+1, . . . , n }
besucht, und schließlich zur Stadt 1 zurückkehrt.
{ 2, . . . , n } führt, dann alle restlichen Städte { 2, . . . , i-1, i+1, . . . , n }
besucht, und schließlich zur Stadt 1 zurückkehrt.
Sei i eine beliebige Stadt und A eine Menge von Städten. Dann definiere L(i,A) als die Länge eines kürzesten Weges
- der in der Stadt i beginnt,
- jede Stadt in der Menge A genau einmal besucht,
- und in Stadt 1 endet.
Für die Berechung der L(i,A)-Werte sind folgende Beobachtungen nützlich.
- Für jede Stadt i
 S ist L(i,
S ist L(i,  ) = DIST [i, 1].
) = DIST [i, 1].
Es ist klar, dass der kürzeste Weg von i nach 1, der keine andere Stadt besucht, die direkte Verbindung von i nach 1 ist. - Für jede Stadt i
 S und Teilmenge A
S und Teilmenge A  S \ {1, i}:
S \ {1, i}:
L(i,A) = min{DIST [i, j] + L(j, A \ {j}) | j A }.
A }.
Wenn die Menge A nicht leer ist, dann kann man den optimalen Weg wie folgt rekursiv definieren. Probiere für alle j A den Weg aus, der von i aus zunächst nach j führt.
Für den besten dieser Wege muss gelten, dass auch der Rest des Weges (von j nach 1)
optimal ist. Dieser hat aber nach unserer Definiton die Länge L(j, A \ {j}).
A den Weg aus, der von i aus zunächst nach j führt.
Für den besten dieser Wege muss gelten, dass auch der Rest des Weges (von j nach 1)
optimal ist. Dieser hat aber nach unserer Definiton die Länge L(j, A \ {j}). - L(1, { 2, . . . , n }) ist die Länge einer optimalen Rundreise.
Dies folgt aus der Tatsache, dass jede Rundreise in der Stadt 1 beginnt, dann alle anderen Städte besucht und schließlich nach 1 zurückkehrt.
Aus diesen Beobachtungen folgt ein rekursiver Algorithmus, der die Werte von L(i, A) für
immer größere Teilmengen A in eine Tabelle einträgt. Dabei ist der Fall A =  die Verankerung
der Rekursion.
die Verankerung
der Rekursion.
Algorithmus TSP mit dynamischer Programmierung
Der Algorithmus füllt eine Tabelle mit n Zeilen (i = 1, . . . , n) und maximal 2n Spalten (für alle Teilmengen der Größe k <= n-1), d.h. die Tabelle enthält maximal n · 2n Einträge. Pro Eintrag wird eine Minimumssuche über n Werte ausgeführt (Zeilen 4 bis 7). Damit wird Zeile 6 des Algorithmus maximal n · n · 2n = n2 · 2n mal ausgeführt.
n Städte |
Größe der Tabelle (n2 · 2n) |
Laufzeit |
3 |
72 |
72 msec |
4 |
256 |
0,4 sec |
5 |
800 |
0,8 sec |
6 |
2304 |
2,3 sec |
7 |
6272 |
6,3 sec |
8 |
16.384 |
16 sec |
9 |
41.472 |
41 sec |
10 |
102.400 |
102 sec |
11 |
247.808 |
4,1 Minuten |
12 |
589.824 |
9,8 Minuten |
13 |
1.384.448 |
23 Minuten |
14 |
3.211.264 |
54 Minuten |
15 |
7.372.800 |
2 Stunden |
16 |
16.777.216 |
4,7 Stunden |
Tabelle 2 zeigt, wie sich diese Zahl mit wachsendem n entwickelt. Außerdem gibt sie in der letzten Spalte eine Abschätzung für die Laufzeit, wenn wir annehmen, dass die Berechnung eines Tabelleneintrags eine Millisekunde Zeit kostet. Man sieht, dass die Laufzeit immer noch mehr als exponentiell mit n wächst. Allerdings ergibt sich im Vergleich zur Holzhammer-Methode doch schon eine gewaltige Verbesserung. Die Zeit zur Berechnung einer optimalen Rundreise durch 16 Städte hat sich von 20 Jahren auf 5 Stunden verringert. Hinweis: Ein ernstes Problem beim Dynamischen Programmieren ist die exponentiell wachsende Tabelle und der damit verbundene Speicherbedarf.
Näherungslösungen
Der Ansatz des Dynamischen Programmierens hat zwar eine Verbesserung der Laufzeit bewirkt. Aber diese ist immer noch exponentiell und daher für große Werte von n völlig unbrauchbar. Auch der gewaltige Speicherbedarf ist ein Problem. In diesem Abschnitt lernen wir ein Verfahren kennen, das nicht unbedingt die optimale Rundreise findet, aber eine relativ gute Lösung berechnet. Genauer gesagt, der nun vorgestellte Algorithmus findet eine Rundreise, die nicht mehr als doppelt so lang wie die kürzeste Reise ist. Ein solches Verfahren nennt man auch eine Heuristik.

Wir modellieren hierzu TSP als ein Problem auf einem Graphen, wobei die Knoten die Städte darstellen und eine Kante zwischen zwei Knoten i und j die direkte Reise von i nach j beschreibt und entsprechend mit der Distanz bzw. den Kosten für diese Reise beschriftet ist. Da beim TSP-Problem für jedes Paar (i, j) von Städten eine direkte Reise von i nach j möglich ist, handelt es sich bei dem so konstruierten Graphen G = (V, E) um den vollständigen Graphen, der alle Knotenpaare als Kanten enthält, d.h. E = V × V . Eine Rundreise wird in diesem Modell durch einen Kreis in G dargestellt, der jeden Knoten genau einmal enthält. Ein solcher Kreis wird auch als Hamilton-Kreis bezeichnet.
Es gibt einen einfachen Zusammenhang zwischen möglichen Rundreisen (d.h. Hamilton-Kreisen) und speziellen Teilgraphen von G, den sogenannen aufspannenden Bäumen. Ein
aufspannender Baum ist ein kreisfreier Teilgraph, der alle Knoten von G miteinander verbindet. Ein minimal aufspannender Baum ist ein aufspannender Baum, dessen Gesamtkosten
(d.h. die Summe aller Kantenkosten) minimal sind.
Wenn man aus einer Rundreise eine beliebige Kante entfernt, so erhält man einen sogenannten
Hamilton-Pfad. Da ein Hamilton-Pfad die Bedingungen eines aufspannenden Baumes erfüllt
(ein kreisfreier Teilgraph, der alle Knoten miteinander verbindet), sind dessen Gesamtkosten
mindestens so groß wie die eines minimal aufspannenden Baumes. Mit anderen Worten, die
Gesamtkosten eines minimal aufpannenden Baumes sind kleiner oder gleich den Gesamtkosten
eines bestmöglichen Hamilton-Pfades und damit auch einer optimalen Rundreise.

Algorithmen zur Berechnung eines minimal aufspannenden Baumes wurden im Rahmen des Algorithmus der Woche bereits im Algorithmus der Woche 21 behandelt. Diese Algorithmen sind sehr effizient. Der teuerste Schritt ist das Sortieren der Kanten nach ihren Kosten. Ausgehend von einem minimal aufspannenden Baum kann man nun sehr leicht eine TSP-Tour berechnen. Das vollständige Verfahren wird in den folgenden Schritten beschrieben. Die dazugehörigen Abbildungen wurden mit einem Programm erzeugt, das man hier herunterladen kann.
Algorithmus:
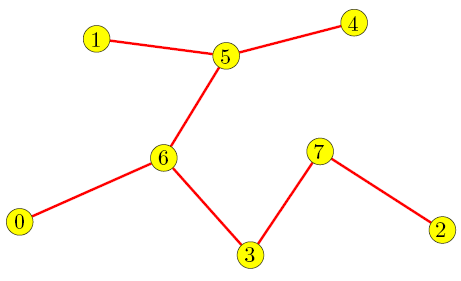
- Konstruiere den vollständigen Graphen G = (V, E) wobei V die Menge der Städte ist und E = V × V (siehe Abbildung 2).
- Berechne einen minimal-aufspannenden Baum T von G. Dabei sind die Kosten einer Kante (v, w) gleich der Entfernung zwischen den Städten v und w (DIST [v, w]). Abbildung 3 zeigt das Ergebnis dieses Rechenschrittes für unser Beispielproblem.
- Im nächsten Schritt konstruiert man aus dem Baum T eine erste Tour, indem man T einfach entlang seiner Kanten einmal umrundet (siehe Abbildung 4). Die Gesamtlänge dieser Reise ist offensichtlich genau doppelt so groß ist wie die Kosten von T, da man jede Kante zweimal verwendet. Aus unseren Vorüberlegungen schließen wir, dass die Gesamtlänge dieser Reise höchstens doppelt so groß wie die Länge einer optimalen TSP Rundreise ist.
- Die im letzten Schritt konstruierte Tour ist offensichtlich nicht optimal und eigentlich
sogar keine korrekte Rundreise, da sie jeden Knoten zweimal besucht. Man kann sie aber leicht in eine korrekte und im allgemeinen auch kürzere Rundreise umwandeln, indem
man jeweils drei aufeinanderfolgene Knoten a, b, c untersucht und testet, ob man die
beiden Kanten a
 b
b  c durch die Abkürzung a
c durch die Abkürzung a  c ersetzen kann, ohne dass der
Knoten b isoliert wird. Das Resultat dieses Schrittes sehen wir in Abbildung 5.
c ersetzen kann, ohne dass der
Knoten b isoliert wird. Das Resultat dieses Schrittes sehen wir in Abbildung 5.
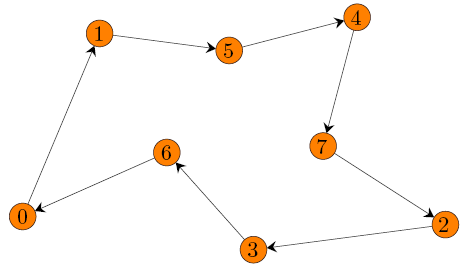
Tabelle 3 zeigt die Laufzeit des MST-Algorithmus für zufällig ausgewählte Städte. Wie man
sieht, kann er eine Näherungslösung für 1000 Städte in etwa einer Minute Rechenzeit finden.
In weiteren Bearbeitungsschritten kann man, die Rundreise weiter verbessern. Es existieren
viele Heuristiken, um dies zu erreichen, z.B. das 2-OPT Verfahren, das wie folgt arbeitet.
Man betrachtet jeweils 2 Kanten der berechneten Tour, sagen wir A ![]() B und C
B und C ![]() D.
Wenn man diese beiden Kanten entfernt, zerfällt die Tour in zwei Teilstücke von B nach C und
von D nach A. Dann wird getestet, ob man diese Teile durch Einfügen der Kanten A
D.
Wenn man diese beiden Kanten entfernt, zerfällt die Tour in zwei Teilstücke von B nach C und
von D nach A. Dann wird getestet, ob man diese Teile durch Einfügen der Kanten A ![]() C und D
C und D ![]() B zu einer kürzeren Tour zusammenfügen kann.
B zu einer kürzeren Tour zusammenfügen kann.
Städte |
Laufzeit |
100 |
0,01 sec |
200 |
0,08 sec |
300 |
0,36 sec |
400 |
1,30 sec |
500 |
3,62 sec |
600 |
8,27 sec |
700 |
16,07 sec |
800 |
29,35 sec |
900 |
50,22 sec |
1000 |
85,38 sec |
Einige Bemerkungen zum Schluss:
- Es gibt eine Reihe weiterer Heuristiken, die oft zu sehr guten Ergebnissen führen und häufig sogar die optimale Rundreise liefern.
- Auch bei der Berechnung von exakten Lösungen für TSP hat man in den letzten Jahren erhebliche Fortschritte erzielt. Es gibt mittlerweile Programme die TSP-Probleme mit mehreren tausend Städten in wenigen Stunden Rechenzeit exakt lösen können.
- Im schlechtesten Fall bleibt das TSP-Problem sehr schwierig (NP-vollständig) und erfordert exponentiell viele Rechenschritte.
- Druckversion des Beitrags (pdf)
- Ein Demo-Programm, mit dem die Abbildungen dieses Artikels erzeugt wurden
- Wikipedia: Problem des Handlungsreisenden
- Eine Einführung von Grötschel und Padberg (Spektrum der Wissenschaft)

