Algorithmus der Woche

• » Startseite
• » aktueller Algorithmus
• » Liste der Algorithmen

Informationen

• » Infoflyer Presse
• » Infoflyer Schule
• » Download Logo

Gimmicks für's Klassenzimmer

• » Visuelle Kryptographie

Links

• » Informatikjahr
• » Fakultätentag Informatik

Intern

• » Für Autoren
• » Für Organisatoren
• » Buchprojekt

Sonstiges

• » Impressum
• » Gästebuch
• » Haftung

Zum Aufwärmen: Fußball

Diese Woche wird es bei unserem Algorithmus um die Berechnung von physikalischen Effekten gehen. Computer können nämlich auch verwendet werden, um natürliche Vorgänge zu simulieren. Das wird in der Wissenschaft immer wichtiger, weil man damit oft besser verstehen kann, wie die Natur funktioniert. Unsere Wettervorhersage beruht z.B. auf einer Simulation, bei der es auf die möglichst genaue Abbildung der Natur im Computer ankommt. Neue Automodelle und Flugzeuge werden auch simuliert, lange bevor sie zum ersten mal gebaut werden. Viele Wissenschaftler sind sogar ganz auf die Simulation angewiesen. Astronomen, die wissen wollen was geschieht, wenn zwei schwarze Löcher zusammenstossen, müssen Computersimulationen verwenden, denn Experimente sind dazu natürlich nicht möglich. Auch Computerspiele sind übrigens oft Simulationen, nur dass es bei Spielen nicht unbedingt darauf ankommt, dass die Berechnungen mit der realen Welt überein stimmen.

Mit unserem Algorithmus werden wir zumindest ein wichtiges Problem simulieren können, nämlich das der Wämeverteilung, wie man sie z.B. für die Wettervorhersage auch braucht. Allerdings werden wir uns auf feste Gegenstände wie beispielsweise eine zweidimensionale Platte beschränken, weil es für die Simulation am Anfang leichter ist, wenn man die Strömung der Luft nicht mit berücksichtigen muss. Bevor wir zur eigentlichen Aufgabe kommen, machen wir erst mal eine „Aufwärmübung“ und schauen uns beim Fußball um.

Bei der letzten WM hat zwar schon nicht viel gefehlt, aber in der kommenden Europameisterschaft steht die Nationalmannschaft endlich doch im Finale. Die Spieler sind ganz aufgeregt, so aufgeregt, dass der Trainer davon überzeugt ist, dass sie es schon nicht schaffen werden, sich zur Nationalhymne in einer Reihe aufzustellen.

Nachdem der Trainer das Spielfeld nicht betreten darf, wo er die Spieler ohne Weiteres selbst auf ihre Plätze in der Reihe stellen könnte, überlegt er sich voller Verzweiflung folgende Vorgehensweise: den beiden Spielern mit den Nummern 1 und 11, die am weitesten rechts und links stehen werden, schärft er ein, nur darauf acht zu geben, dass die übrigen Spieler noch zwischen ihnen Platz haben. Ansonsten sollen sie sich nicht mehr von der Stelle rühren.

Die restlichen Spieler mit den Nummern 2 bis 10 erhalten folgende Anweisung: wenn sie aufgerufen werden, sollen sie sich so bewegen, dass sie genau in der Mitte zwischen ihrem rechten und linken Nachbarn stehen. Der Trainer ruft nacheinander alle Spieler in der Reihenfolge ihrer Trikotnummern auf, und nachdem sich der Spieler mit der höchsten Nummer bewegt hat, fängt der Trainer wieder von vorne an.

Siehe da: nach einigen Durchläufen dieses Verfahrens haben sich die Spieler tatsächlich so bewegt, dass sie zumindest einigermaßen in einer Reihe stehen. Ganz genau stimmt es zwar nicht, aber es ist gut genug, dass keiner etwas merkt.

Um die Spieler ganz genau auf die Linie zu bekommen, müsste man den Algorithmus unendlich lange laufen lassen. Deshalb bekommt man in der Praxis nie das ganz richtige Resultat. Aber das macht nichts, weil schon nach genügend vielen Schritten das Ergebnis gut genug ist. Solche Algorithmen findet man häufig, wenn es um sogenannte numerische Probleme geht, also dort, wo echte Kommazahlen ausgerechnet werden, wie man sie z.B. als Physiker oder Ingenieur braucht.

Wenn sich die Spieler in der Reihenfolge ihrer Trikotnummern aufstellen, dann sagt man, dass sie lexikographisch sortiert stehen. Wir haben sie also immer wieder von links nach rechts aufgerufen, aber das hätten wir auch anders machen können. Eine beliebte Variante ist die sogenannte Rot-Schwarz-Sortierung der Spieler. Dabei belegt die Hälfte der Spieler mit den niedrigen Trikotnummern zunächst jeden zweiten Platz in der Reihe, anschließend füllen die Spieler mit den hohen Trikotnummern die restlichen Plätze auf. Aber auch, wenn die Spieler sich komplett zufälig aufstellen, funktioniert das Verfahren, es muss nur immer für jeden Spieler klar sein, welches seine beiden Nachbarn sind.

Temperaturberechnung in einem Stab (1D)

Jetzt kommen wir nun wirklich zur Berechnung einer Temperaturverteilung. Ist es nicht ein bisschen erstaunlich, dass wir auch dazu das Prinzip des Sich-in-einer-Reihe-Aufstellens verwenden können? Will man z.B. die Temperaturverteilung in einem dünnen Stab berechnen, stellt man nämlich fest, dass die Temperatur an jeder Stelle des Stabes dem Mittelwert der benachbarten Temperaturen entsprechen muss. Fixiert man die Temperatur an den beiden Enden des Stabes, dann verläuft die Temperatur zwischen den beiden Enden „in einer Reihe“, also linear vom einen zum anderen Ende.

Um diese lineare Verteilung zu berechnen, braucht man mit Sicherheit noch keinen Computer, genau so wenig, wie ein Fußballtrainer normal keinen komplizierten Algorithmus braucht, um die Spieler in einer Reihe aufzustellen. Aber wir sehen, dass die Probleme verwandt sind und sich vielleicht auf gleiche Weise lösen lassen. Die Position des Spielers entspricht dem Temperaturwert, und ansonsten verläuft die Berechnung auf gleiche Weise wie bei unserem Fußballproblem.

Als nächstes machen wir die Aufgabe noch etwas interessanter: wie sieht es denn mit dem Temperaturverlauf aus, wenn man den Stab zusätzlich an einer Stelle in der Mitte erhitzt? Dann gilt für die Temperatur an dieser Stelle natürlich nicht mehr, dass sie dem Durchschnitt der benachbarten Temperaturen entspricht, hinzu kommt ja noch die zusätzliche Erwärmung.

Jetzt gibt es keine offensichtliche Möglichkeit mehr, den resultierenden Temperaturverlauf zu bestimmen, also überlegen wir uns, wie wir den Computer zur Lösung dieses Problems benutzen können. Eine erste Schwierigkeit ergibt sich aus der Tatsache, dass entlang des Stabes unendlich viele Punkte liegen, jeder Computer aber nur einen endlichen Speicher besitzt. Wir wählen daher entlang des Stabes eine endliche Anzahl an Punkten aus, an denen wir die Temperatur berechnen wollen. Diese Vorgehensweise nennt man auch Diskretisierung, da man ein kontinuierliches Problem auf ein diskretes Problem abbildet.

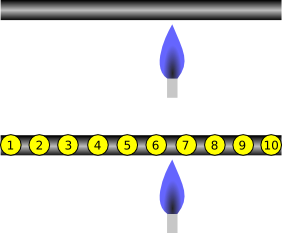
Sind die Punkte gleichmäßig über den Stab verteilt, dann wird die Temperatur an einem Punkt aktualisiert über die Formel

Wert an Punkt i := 1/2 * (Wert an Punkt i-1 + Wert an Punkt i+1) + Erhitzung an Punkt i

Wie im Beispiel der Fußballspieler werden nur die Punkte im Inneren des Stabes laufend neu berechnet, an den beiden Punkten am Rand des Stabes nimmt man die Temperatur als gegeben an. Je nach dem physikalischen Experiment, kann es aber auch sein, dass die Stabenden isoliert sind. Wir haben auch noch nicht überlegt, dass der Stab in der Praxis Wärme an seine Umgebung abgibt. Das kann man durch enstprechend kompliziertere Formeln und Berechnungen mit berücksichtigen, die uns jetzt aber zu weit führen würden. Statt dessen sehen wir uns eine andere Schwierigkeit an, die sich ergibt, wenn wir nicht einen eindimensionalen Stab, sondern eine zweidimensionale Platte berechnen wollen.

Temperaturberechnung auf einer Platte (2D)

Wir können die Aufgabenstellung erweitern, indem wir keinen eindimensionalen Stab, sondern eine zweidimensionale Kochplatte betrachten, die vielleicht wiederum an bestimmten Stellen erhitzt wird.

Die Diskretisierung funktioniert ähnlich wie im obigen Fall, diesmal ergibt sich ein zweidimensionales Gitter von Punkten. An diesen Punkten soll die Temperatur berechnet werden. Für die Mittelung der Nachbartemperaturen an einem Punkt darf man jetzt nicht mehr nur die rechten und linken Nachbarn betrachten, sondern muss natürlich auch die oberen und unteren Nachbarn mit dazunehmen.

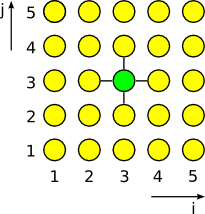
Aufgrund dieser Darstellung der Abhängigkeiten eines Punktes von seinen Nachbarpunkten spricht man von dem Stern, den man auf den Punkt und seine Umgebung anwenden muss, um seinen Wert neu zu berechnen. In diesem Fall handelt es sich also um einen Fünf-Punkt-Stern, und der neue Wert eines Punktes berechnet sich zu

Wert an Punkt (i,j) := 1/4 * (Wert an Punkt (i-1,j) + Wert an Punkt (i+1,j) + Wert an Punkt (i,j-1) + Wert an Punkt (i,j+1) + Erhitzung an Punkt (i,j))

Betrachten wir ein Beispiel, in dem am rechten Rand ein kurvenförmiger Temperaturverlauf und an allen anderen Rändern die Temperatur Null vorgegeben ist. Dabei stellen wir die Temperatur als Wert in der dritten Dimension in Abhängigkeit von der Position auf der Platte dar. In diesem dreidimensionalen Bild sieht man also eine Landschaft, deren Höhe der Temperatur an diesem Punkt entspricht. Das erste Bild zeigt damit eine Temperaturverteilung, bei der an allen Punkten eines Gitters mit 33 x 33 Punkten die Temperatur 0 ist, ausgenommen an dem rechten Rand. Dort ist eine Temperaturkurve vorgegeben.

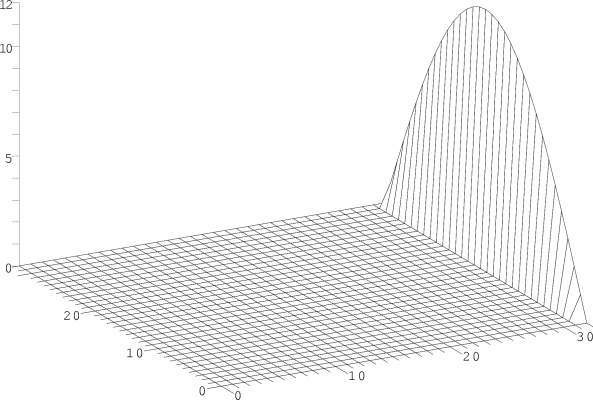
Dies entspricht nicht der richtigen Temperaturverteilung, die wir ja erst mit unserem Gauß-Seidel-Verfahren ausrechnen wollen. Am Ende muss eine glatte Temperaturverteilung herauskommen, die aber anders als im eindimensionalen Stab nicht mehr linear ist, selbst wenn es keine zusätzlichen Temperaturquellen gibt.

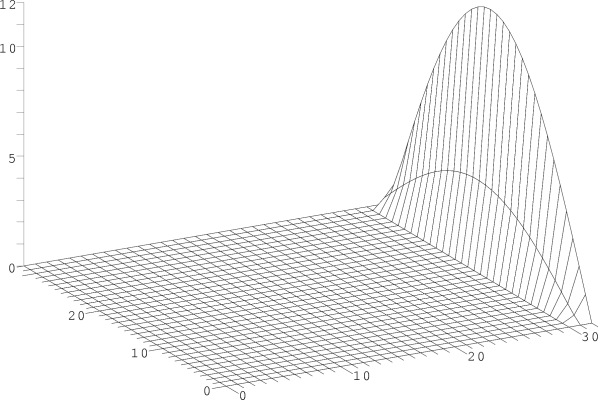
Lässt man nun einige Gauß-Seidel-Iterationen laufen, dann erkennt man, wie die am Rand vorgegebene Temperatur in das Innere der Platte hineinwandert, bis die Temperaturverteilung über der ganzen Platte schließlich schön glatt aussieht. Der Rechenaufwand ist übrigens nicht ohne, denn jeder Durchlauf des Gauß-Seidel-Verfahrens muss ja an 31 x 31 = 961 Punkten den Durchschnitt von vier Zahlen berechnen. Bei Tausend Durchläufen hat der Computer deshalb fast schon 5 Millionen Rechenoperationen zu bewältigen.

Nach einer Iteration
Nach zwei Iterationen
Nach zehn Iterationen
Nach 100 Iterationen
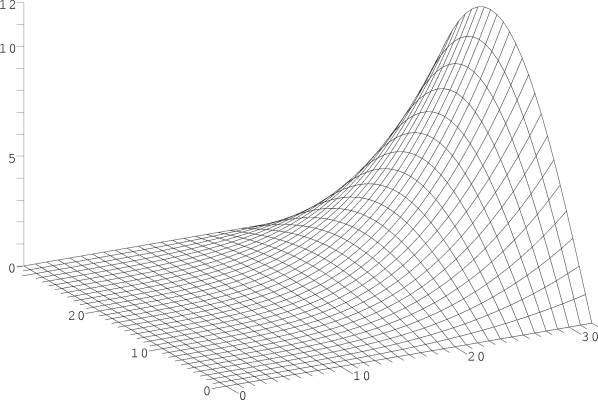
Nach 1000 Iterationen

Auch wenn nach 100 Iterationen die berechnete Lösung auf den ersten Blick schon recht gut erscheint, darf man das Verfahren an dieser Stelle noch nicht abbrechen, wie folgende Bilder zeigen. Das erste Bild zeigt die exakte Lösung des Problems (die man in diesem Sonderfall mit mathematischen Formeln ausrechnen kann), im zweiten Bild werden diese exakte Lösung und die nach 100 Gauß-Seidel-Durchläufen übereinander gezeigt, so dass man schön sehen kann, dass das Ergebnis noch nicht wirklich stimmt.

Exakte Lösung
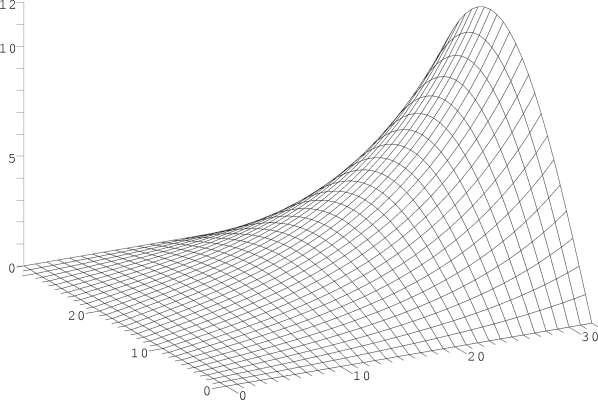
Unterschied nach 100 Iterationen
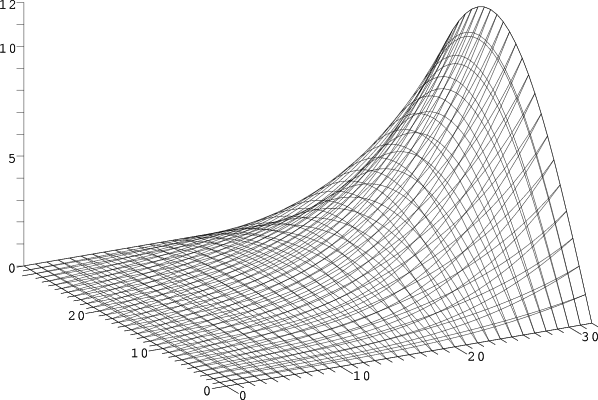
Unterschied nach 1000 Iterationen

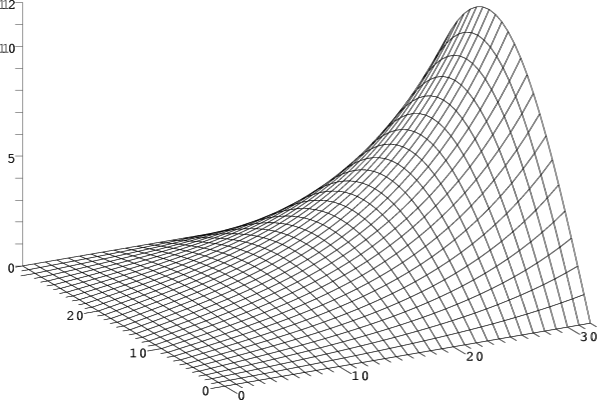
Erst nach ungefähr 1000 Durchläufen zeigt die Überblendung keinen Unterschied zwischen exakter und berechneter Lösung mehr.

Das folgende Java-Applet ermöglicht, den Temperaturverlauf bei unterschiedlichen Erhitzungen zu berechnen. Die Temperatur wird hier farbkodiert, blau bedeutet eine niedrige Temperatur, rot eine hohe Temperatur.

Auch wenn es so aussieht, als ob bei der Temperaturverteilung der zeitliche Fortschritt der Erhitzung dargestellt werden würde, ist dies nicht der Fall. Was hier berechnet wird, ist der Zustand, wenn das System bei der gegebenen Erhitzung im Gleichgewicht ist. Mit anderen, etwas komplizierteren Verfahren kann man auch berechnen, wie sich der zeitliche Verlauf der Erwärmung oder Abkülung verhält.

Bei der Temperaturberechnung in einer Platte könnte man übrigens noch argumentieren, dass man die Temperatur mit einem Thermometer, das man an die Platte hält, auch im Experiment leicht bestimmen könnte und die Simuliererei damit ja überflüssig ist. Die Temperaturbestimmung im Inneren eines festen dreidimensionalen Objekts, z.B. einem Ziegelstein, der bei hohen Temperaturen gebrannt wird, ist experimentell dann schon nicht mehr möglich, ohne ihn zu zerstören.

Eine interessante Frage ist natürlich, wie viele Durchläufe des Gauß-Seidel-Verfahrens benötigt werden, um eine gute Näherung der physikalischen Lösung zu berechnen. Durch die Erfahrung (oder besser durch eine mathematische Analyse des Algorithmus) bekommt man heraus, dass bei einem Gitter mit NxN Punkten ungefähr NxN Durchläufe gemacht werden müssen. Weil andererseits die Temperatur in der Platte um so genauer wiedergegeben werden kann, je feiner die Gitterpunkte liegen, bekommt man schnell einen Rechenaufwand, der auch moderne PCs überfordert. Das gilt vor allem dann, wenn man nicht zweidimensionale Gebilde (wie die Platte) sondern dreidimensionale Objekte simulieren möchte, und zusätzliche physikalische Phänomene - wie bei der Wettervorhersage - die Berechnungen komplizierter machen. Dann braucht man einerseits schnelle Supercomputer, die vielleicht viele Millionen Euro teuer sind, und auch noch bessere Algorithmen, die das gleiche Resultat viel schneller ausrechnen können. Die teuersten und schnellsten Computer der Welt werden jedes halbe Jahr neu in der TOP-500 Liste veröffentlicht. Diese Supercomputer werden fast ausschließlich für numerische Simulationen von komplizierten wissenschaftlichen Fragestellungen eingesetzt, bei denen das Gauß-Seidel-Verfahren und seine Varianten zum Einsatz kommen. Supercomputer sind damit sozusagen die Play-Stations für Wissenschaftler.

Wer sich noch dafür interessiert, hier sind zwei Ideen, wie man den Algorithmus beschleunigen kann: In den obigen Bildern sieht man, dass die richtige Lösung von einer Seite her angenähert wird, nämlich von unten. Anders gesagt, jeder Gauß-Seidel-Durchlauf bringt uns näher an die richtige Lösung, aber er geht nicht weit genug. Das kann man ausnützen, indem man in jeder der einzelnen Berechnungen die Änderung entsprechend vergrößert, d.h. mit einer Zahl größer 1 (aber kleiner 2) multipliziert. Wenn man einen guten Vergrößerungsfaktor gefunden hat, dann erreicht man viel schneller die richtige Lösung. Diese Berechnungsweise ist das sogenannte SOR-Verfahren (engl: successive over relaxation).

Die zweite Idee ist noch komplizierter und beruht darauf, dass Gitter mit verschiedenen Punktabständen kunstvoll zusammenarbeiten. Dieses sogenannte Mehrgitterverfahren kommt dann mit einer sehr geringen Anzahl von Durchläufen aus und gilt als das schnellste Verfahren für diese Art von Problemen. Da sind wir dann allerdings schon mitten in der Forschung. Wer sich dafür interessiert, findet auf der Seite der Zeitschrift Computing in Science and Engineering einen kostenlosen englischen Artikel Why Multigrid Methods Are so Efficient , der sehr gut geschrieben ist, aber schon ein bisschen mehr Mathematik erfordert.

Zu guter Letzt sei gesagt, dass das Gauß-Seidel-Verfahren von dem berümtesten aller Mathematiker, nämlich Carl Friedrich Gauß, 1823 erfunden wurde und von einem seiner Kollegen, Philipp Ludwig Seidel, in der Folge weiter entwickelt wurde. Damals wurde natürlich von Hand gerechnet. Gauß schreibt in einem Brief „Das Verfahren läßt sich halb im Schlaf ausführen oder man kann während dessen an andere Dinge denken.“ Wenn man das Verfahren heute programmiert, können auch wir an andere Dinge denken, während Computer die Rechenarbeit machen.