Autoren
Prof. Dr. K. Rüdiger Reischuk, Universität zu Lübeck
Dipl. Inf. Markus Hinkelmann, Universität zu Lübeck
Die bisherigen Algorithmen der Woche haben ein
Problem schnell oder, wie man sagt, effizient gelöst.
Wenn man nun für ein Problem keinen schnellen Algorithmus findet,
ist dies eigentlich ein Grund, unzufrieden zu sein. Dieses Mal
überlegen wir, wieso es manchmal von Vorteil
ist, wenn ein Problem keinen schnellen Algorithmus besitzt.
Unser heutiges Motto könnte also lauten:
Im letzten Beitrag haben wir gesehen, dass das Produkt von Zahlen
recht schnell berechnet werden kann, auch wenn die Zahlen sehr groß
sind und damit viele Ziffern für ihre Darstellung im Dezimal- oder
Binärsystem
benötigen. Selbst mit dem simplen Algorithmus, der in der Grundschule
gelehrt wird,
kann ein Mensch zwei größere Dezimalzahlen auf einem großen Blatt
Papier
in ein paar Minuten multiplizieren, auch wenn dies mühsam ist und
Konzentration bedarf, um Rechenfehler zu vermeiden. Für einen Computer
ist es überhaupt kein Problem, hundert- oder tausendziffrige Zahlen
innerhalb von Sekundenbruchteilen zu multiplizieren oder zu dividieren.
Betrachten wir nun das umgekehrte Problem, ein Produkt wieder in seine Faktoren zu zerlegen. Man lernt in der Schule, dass es Primzahlen gibt, die man nicht mehr in Faktoren zerlegen kann. Jeder kennt die ersten Primzahlen: 2, 3, 5, 7, 11, 13, 17, 19, 23, ... Die Erfahrung zeigt, dass jede natürliche Zahl auf eindeutige Weise in Primfaktoren zerfällt wie beispielsweise
und das kann man auch beweisen. Bei Primzahlen selber besteht dies Produkt nur aus einem Faktor. Hier ergibt sich in natürlicher Weise die Frage nach einem Algorithmus für das Problem, zu einer gegebenen großen Zahl ihre Primfaktoren zu bestimmen, das Faktorisierungsproblem. Geht das vielleicht auch so schnell wie Multiplizieren?
Ob eine Dezimalzahl n durch 2 bzw. 5 teilbar ist, erkennt man mit einem Blick an der letzten Ziffer; Teilbarkeit durch 3 überprüft man mit dem Quersummentest. Einen ähnlich einfachen Test gibt es auch noch für die Teilbarkeit durch 11. Das Faktorisieren von vielziffrigen Zahlen, die nur große Teiler besitzen, scheint dagegen sehr schwer zu sein. Man könnte n durch jede Primzahl p mit p2 ≤ n zu teilen versuchen. Es ist bekannt, dass dies bei einer 100-stelligen Zahl ungefähr 8,5 · 1048 Versuchs-Divisionen benötigt — das ist in etwa eine 1 mit 49 Nullen, eine absolut unvorstellbar große Zahl, so dass hieran nicht zu denken ist.
Als eine einfachere Variante des Faktorisierungsproblem können wir das Primzahlproblem ansehen, wo nur festzustellen ist, ob eine Zahl n eine Primzahl oder Nichtprimzahl ist - man muss im zweiten Fall also nicht auch noch die Faktoren herausfinden. Für das Primzahlproblem gibt es effiziente Algorithmen, aber die sollen nicht unser heutiges Thema sein.

In den 70er Jahren haben Ron Rivest, Adi Shamir, and Leonard Adleman ihr inzwischen weit verbreitetes RSA-Kryptosystem erfunden, das Texte verschlüsselt, die man dann versenden kann - auch über so ein unsicherer Medium wie das Internet, so dass ein unbefugter Mithörer die Nachricht nicht verstehen kann. In dem System wird eine Zahl n benutzt, die Produkt zweier sehr großer Primzahlen p und q ist. Man weiß, dass das Knacken dieses Verschlüsselungsverfahrens sehr eng zusammenhängt mit dem Problem, die beiden Faktoren p und q von n herauszufinden.
Um zu demonstrieren, wie sicher ihr System ist, haben die Erfinder 1977 eine Nachricht mit einer 129-stelligen Dezimalzahl n verschlüsselt und n und die verschlüsselte Nachricht veröffentlicht.

Es dauerte unglaubliche 17 Jahre, bis 1994 sehr komplizierte Algorithmen entwickelt worden waren, die Intelligenteres tun als einfach alle möglichen Primteiler auszuprobieren, und dann noch 8 Monate Rechenzeit auf einem weltweiten Netz von Hunderten von Computern, um die beiden Faktoren
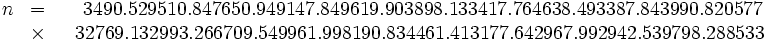
herauszufinden. Insgesamt wurden dabei etwa 160 Billiarden Computerbefehle ausgeführt, das sind 1,6 · 1017. Wollt Ihr wissen, wie die verschlüsselte Nachricht hieß? Weitere Informationen findet man beispielsweise unter: http://www.wired.com/wired/archive/4.03/crackers.html?pg=4&topic=
Auch heutzutage, weitere 12 Jahre später, gilt weiterhin
- die schlechte Nachricht:
 Selbst mit den besten
zur Zeit verfügbaren Algorithmen
und den schnellsten zur Zeit oder in den nächsten Jahren verfügbaren
Superrechnern, auch mit Tausenden oder Zigtausenden von Computern kann
man für Dezimalzahlen mit mehreren hundert Stellen, die nur sehr große
Primfaktoren besitzen,
diese Faktoren nicht herausfinden;
Selbst mit den besten
zur Zeit verfügbaren Algorithmen
und den schnellsten zur Zeit oder in den nächsten Jahren verfügbaren
Superrechnern, auch mit Tausenden oder Zigtausenden von Computern kann
man für Dezimalzahlen mit mehreren hundert Stellen, die nur sehr große
Primfaktoren besitzen,
diese Faktoren nicht herausfinden;
- die gute Nachricht:
 Solange keine dramatisch schnelleren Faktorisierungsalgorithmen
zur Verfügung stehen, können Daten wie z.B. beim online-Banking,
die mit modernen kryptografischen Verfahren basierend auf dem
RSA-Schema oder Ähnlichem verschlüsselt werden, als sicher angesehen
werden.
Solange keine dramatisch schnelleren Faktorisierungsalgorithmen
zur Verfügung stehen, können Daten wie z.B. beim online-Banking,
die mit modernen kryptografischen Verfahren basierend auf dem
RSA-Schema oder Ähnlichem verschlüsselt werden, als sicher angesehen
werden.

Halten wir also fest:
- die Multiplikation natürlicher Zahlen, insbesondere von Primzahlen, lässt sich effizient berechnen,
- ihre Umkehrung, die Zerlegung einer Zahl in ihre Primteiler, dagegen nicht - zumindest nach dem heutigen Erkenntnisstand der Informatik und Mathematik.
In der Mathematik versteht man unter dem Begriff Funktion eine Operation, die mathematische Objekte in andere derartige Objekte transformiert. Die Faktorisierung kann man als die zur Multiplikation umgekehrte Operation ansehen. Eine derartige Operation, die leicht zu berechnen ist,aber eine schwierige Umkehroperation hat, wollen wir eine Einweg-Funktion nennen. Einweg-Funktionen haben für die Verschlüsselung von Texten eine wichtige Bedeutung. Die Verschlüsselung könnte mit Hilfe einer Einweg-Funktion geschehen. Denn diese Operation sollte schnell ausführbar sein; die Entschlüsselung, die Umkehroperation, dagegen sollte schwierig sein. Dies sind aber gerade die Eigenschaften, die von einer Einweg-Funktion verlangt werden. Ein unberechtigter Angreifer auf die verschlüsselten Daten hat damit praktisch keine Chance, aus dem verschlüsselten Text das ursprüngliche Dokument zu rekonstruieren.
Betrachten wir folgendes Beispiel: Alice möchte an Bob
den Text "Ziemlich geheim" schicken. Wir deuten Zwischenräume durch "x"
an und verwenden nur Großbuchstaben. Nun verschlüsseln wir
folgendermaßen: Die Buchstaben werden mit 01 bis 26 durchnummeriert,
und jeder Buchstabe wird durch seine Nummer ersetzt. Aus
Nun ist T im allgemeinen keine Primzahl, aber man kann immer
durch Anhängen von ein paar zusätzlichen Ziffern - in diesem Fall z.B.
000257 - eine Primzahl
erhalten. Dann nimmt Alice eine weitere Primzahl, mit etwa ebenso vielen Ziffern, etwa
und bildet das Produkt
Diese Zahl n kann Alice an Bob schicken - niemand wird jetzt in der Lage sein, die Nachricht p bzw. T zu entschlüsseln. (Das funktioniert in Wirklichkeit nicht mit 40-stelligen Primzahlen wie in unserem Beispiel, wenn ein mitlesender Bösewicht Eve gute Faktorisierungsalgorithmen und einen schnellen Computer benutzt. Aber es funktioniert mit 150-stelligen Primzahlen.)
Aber halt ... . Jetzt kann ja auch Bob die Nachricht nicht entschlüsseln! So ein Pech! Ganz so einfach ist die Verschlüsselung mit Einwegfunktionen also auch wieder nicht. Wir brauchen einen zusätzlichen Trick.
Eine Einweg-Funktion mit geheimer Zusatzinformation, in der Fachsprache spricht man auch von einer Falltür- oder Geheimtür-Funktion, besitzt die folgende zusätzliche Eigenschaft:
- Die Umkehr-Funktion von f kann effizient berechnet werden, wenn man im Besitz eines geheimen Schlüssels S ist.
Hierfür gibt es ein ganz unmathematisches Beispiel aus dem täglichen Leben.

Gehen wir einen Schritt zurück in die Vergangenheit, als es noch keine elektronischen Dateien über Telefonanschlüsse gab, sondern nur das gute alte gedruckte Telefonbuch. Wenn Alice ihren alten Freund Bob nach langer Zeit wieder einmal anrufen möchte und seine Telefonnummer nicht mehr zur Hand hat, braucht sie nur im Telefonbuch nach Bobs Namen zu suchen und findet dahinter seine Telefonnummer. Das geht einfach und schnell - warum?
Erinnern wir uns an den ersten Beitrag dieser Reihe, die binäre Suche. Im aktuellen Telefonbuch der Hansestadt Lübeck mit circa N = 250.000 Einträgen (verteilt auf über 700 Seiten) beispielsweise kann man jeden Namen mit höchstens 18 ≈ log2 N vielen Namensvergleichen finden, da die Teilnehmer in alphabetischer Reihenfolge aufgelistet werden. Wären sie dagegen ungeordnet, müsste man jedesmal das Telefonbuch solange durchlesen, bis man auf den gesuchten Namen gestoßen ist, was im Mittel die halbe Buchgröße ausmachen würde und bei 250.000 Einträgen absolut impraktikabel wäre. In der Realität wird allerdings die binäre Suche selten in Originalform angewandt - auch von Informatikern nicht, jeder macht es ein bisschen anders. Wir wissen jedenfalls alle aus Erfahrung: die Suche vom Namen zur Telefonnummer ist einfach - aufgrund der alphabetischen Anordnung.

Wie sieht es mit der umgekehrten Suche aus, zu einer gegebenen Nummer den Teilnehmer zu finden?
Alice findet auf dem Display ihres Telefons die Nachricht, dass jemand mit der Nummer 123456 versucht hat, sie anzurufen. Sie kennt diese Nummer nicht, will aber nicht einfach zurückrufen, sondern erst wissen, wer sich hinter dieser Nummer verbirgt.Mit einem gedruckten Telefonbuch bleibt ihr nichts anderes übrig, als das gesamte Telefonbuch Eintrag für Eintrag durchzukämmen, bis sie die Nummer entdeckt hat. Damit ist, die Zuordnung Name → Nummer eine Art Einweg-Funktion, zumindest für Menschen, denen nur gedruckte Telefonbücher zur Verfügung stehen.
Computer dagegen können mit cleveren Algorithmen eine Folge von Datenpaaren sehr schnell sortieren, wie in vorangegangenen Beiträgen erläutert worden ist, so dass heutzutage manche Informationsanbieter elektronische Telefonbücher nach Nummern geordnet umsortieren. Mit Hilfe solch eines zusätzlichen umgekehrten Telefonbuches führt eine binäre Suche schnell zu dem gesuchten Namen. Im Computerzeitalter könnte man somit auch die Suche nach einem Namen effizient durchführen. Wir wollen jedoch noch einen kleinen Augenblick in der Situation verweilen, dass es nur gedruckte Telefonbücher gibt.
Eine kundenfreundliche Telefongesellschaft könnte Alices Problem dadurch lösen, dass sie Telefonnummer gemäß der alphabetischen Reihenfolge der Namen der Telefonbesitzer vergibt, d.h. Alice erhält eine Nummer mA, die kleiner ist als Bobs Nummer mB, da ihr Name alphabetisch vor dem von Bob kommt. In einem derartigen geordneten Telefonnummervergabesystem kann auch ein Mensch zu jeder Nummer den passenden Teilnehmer in wenigen Sekunden finden - vorausgesetzt er wendet die binäre Suche auf die geordnete Folge der Telefonnummern an.
Das Telefonbuch für ein geordnetes Telefonnummervergabesystem hat damit
die Einweg-Eigenschaft verloren.
Dies gefällt dem Datenschützer Bob jedoch nicht.
Er besteht auf einer chaotischen Verteilung der Telefonnummern, um
seine Telefonnummer nicht für jedermann so leicht zugänglich zu machen,
und wendet sich deshalb an den DSD (Deutscher Sicherheits-Dienst).
Der DSD löst das Problem, indem jeder Teilnehmer eine neue Nummer
bekommt, die sich
durch eine geheim gehaltene Transformation S
errechnet,
so dass die vormals geordnete Folge der Nummern
| mA | mAndreas | mAxel | ... | von Alice, Andreas, Axel, ... nach der Transformation zu |
| S(mA) | S(mAndreas) | S(mAxel) | ... | vollständig chaotisch erscheint. |
Was kann man über dies neue Telefonnummervergabesystemsagen sagen? Im zugehörigen Telefonbuch sind die Teilnehmer alphabetisch geordnet aufgelistet, und dies mit ihren neuen Nummern S(m), die, wenn man S nicht kennt, vollkommen willkürlich angeordnet zu sein scheinen. Alice bleibt also wiederum nichts anderes übrig, als das Telefonbuch linear zu durchsuchen. Der DSD dagegen kann mit Kenntnis der Transformation S aus S(m) die ursprüngliche Nummer im geordneten System zurückberechnen und dann eine binäre Suche auf den zurücktransformierten Nummern ausführen.
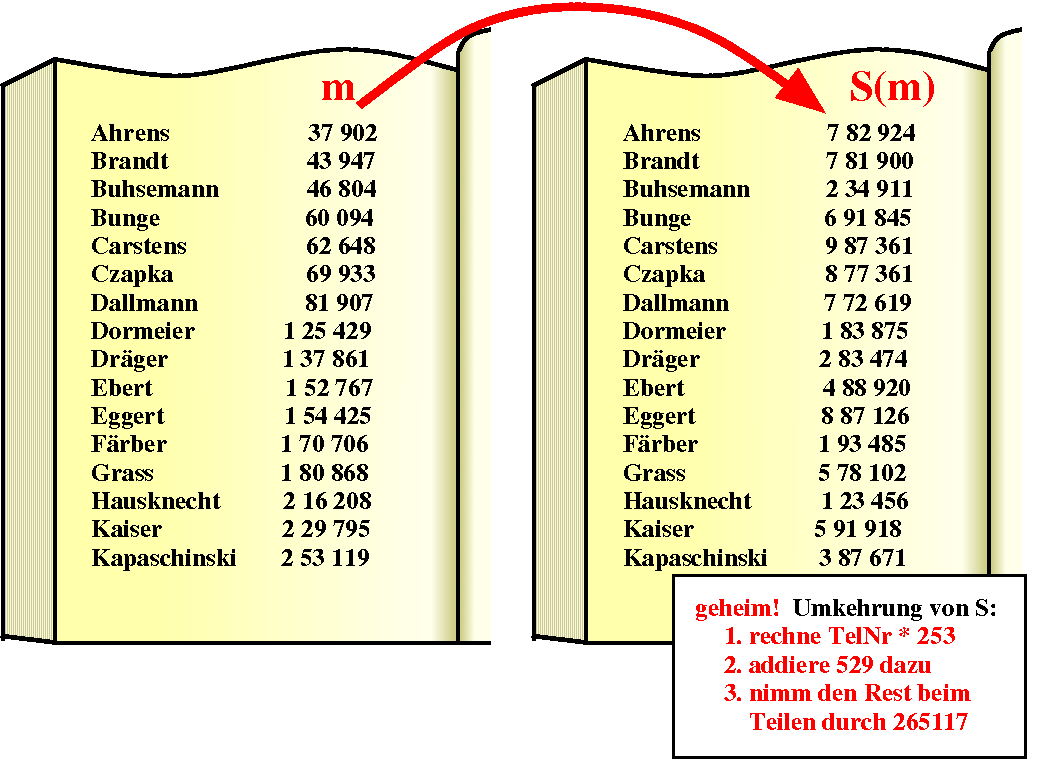
Die Zuordnung Name → Nummer im transformierten Telefonbuch ist somit eine Einweg-Funktion mit Geheimtür. Jeder kann zu einem Namen schnell die passende Nummer finden. Die Umkehrung kann nur derjenige effizient ausführen, der das Geheimnis S kennt.
Gibt es weitere Beispiele derartiger Funktionen, die auch für die schnellsten Computer eine Falltür darstellen? Betrachten wir einmal das folgende Problem, das sich mit Münzen beschäftigt. Bei einer Währung wie dem Euro gibt es verschiedene Münzen und Banknoten, wobei es darauf ankommt, dass man jeden beliebigen Geldbetrag möglichst einfach zusammenstellen kann. Im allgemeinen gibt es verschiedene Möglichkeiten: ein Betrag von 17 Cent kann beispielsweise durch drei 5-Cent- und eine 2-Cent-Münze bezahlt werden, aber auch durch eine 10-Cent und sieben 1-Cent-Münzen. Wir wollen im folgenden nur Zusammenstellungen betrachten, in denen jeder Münzwert höchstens einmal verwendet wird. Wie stelle ich dann fest, ob ich den Betrag X mit lauter verschiedenen Euro-Münzen und Scheinen darstellen kann? 17 Cent lassen sich immer noch als 10+5+2 darstellen, ein Betrag von 19 Cent dagegen nicht.
Algorithmus für das Münzproblem mit einer Menge M von Münzen und einem Betrag X:
| 1 | Wähle die größte Münze m aus M, die den Wert X nicht übersteigt. |
| 2 | Löse das Münzproblem für den Betrag X - m. |
| 3 | Kann man diesen Betrag X - m durch die Münzen m1, ... , mk darstellen, |
| 4 | so gib als Lösung m, m1, ... , mk aus, |
| 5 | andernfalls ein "?". |

|
| supermonotone Folge von Münzen |
Versucht man das gleiche mit X = 79, so verbleibt nach Wahl der Münzen von 50, 20, 5, 2 und 1 ein Restbetrag von 1. Der Wert 79 scheint also nicht erreichbar zu sein. Warum ist diese Vermutung korrekt? Könnte man 79 nicht auch durch eine andere Kombination von Münzen darstellen? Der Grund ist ganz einfach: ordnet man die Münzen der Größe nach beginnend mit dem kleinsten Wert, so ist die Summe der Werte eines Anfangsstücks von Münzen, etwa 1+2+5+10=18 immer kleiner als die nächste Münze, in unserem Fall das 20-Cent-Stück. Eine derartige Folge von Zahlenwerten nennt man supermonoton.
Wenn überhaupt möglich, ist die Darstellung eines Wertes X dann eindeutig, und der obige simple Algorithmus findet die richtige Auswahl sehr schnell. Das Problem wird erheblich schwieriger für Münzfolgen, die nicht supermonoton sind. Unser Algorithmus liefert dann nicht immer die korrekte Antwort.
| Beispiel: X = 101 und
Münzen mit den Werten 7, 10, 28, 35, 38, 56, 64:
x - 64 = 37 und 37 - 35 = 2, es verbleibt also ein Restbetrag von 2. Mit 56+28+10+7 dagegen hätte es geklappt. |
Bei wenigen Münzen kann man natürlich alle möglichen Kombinationen ausprobieren und so eine korrekte Antwort finden. Spätestens bei 100 Münzen ist dies Verfahren aber nicht mehr praktikabel, da die Anzahl der verschiedenen Kombinationsmöglichkeiten, 2100, viel zu groß ist, selbst für schnelle Computer - siehe auch den Beitrag in dieser Reihe zum Rucksackproblem.
Unser Münzproblem ist aber nichts anderes als die Umkehrung des simplen Problems, aus einer Menge von Zahlen eine bestimmte Teilmenge von Zahlen herauszugreifen und diese zu addieren. Auch bei 1000 Münzen kann dies ein Mensch im Prinzip recht einfach per Hand ausrechnen. Wir haben somit wieder eine Einweg-Funktion vor uns.
Wie kann man nun aus dem Münzproblem eine Einweg-Funktion mit
Geheimtür gewinnen, die für kryptografische Zwecke wie oben
skizziert eingesetzt werden könnte?
Wir benutzen eine ähnliche Idee wie beim Telefonbuch.
Starte mit einer supermonotonen Folge, für die das Umkehr-Problem
einfach zu lösen ist, und transformiere die Münzwerte in geeigneter
Weise, so dass die Supermonotonie verschleiert wird. Ohne diese geheime
Information hat ein Angreifer wenig
Chancen, die auszuwählenden Münzwerte auf direkte Weise zu berechnen,
wie wir es oben praktiziert haben.
Diese Idee ist tatsächlich realisiert worden, Details findet man unter
http://www-ee.stanford.edu/ hellman/publications/73.pdf.
Kann man beweisen, dass es für ein konkretes Probleme keine effizienten Algorithmen gibt? Intuitiv wird man vermuten, dass es schwieriger sein dürfte, die Nichtexistenz eines Objektes nachzuweisen als dessen Existenz: Dies gilt sicherlich bei der Suche nach schnellen Algorithmen, denn deren Zahl ist unendlich groß. Um letzte Zweifel an der Sicherheit moderner Kryptosysteme zu zerstreuen, müsste jedoch der Nachweis erbracht werden, dass es für die Umkehr-Funktion des Verschlüsselns keine effizienten Verfahren gibt. Seit über 30 Jahren sucht die Informatik nach Methoden, um zu beweisen, dass bestimmte Probleme keine schnellen Algorithmen besitzen. Obwohl dabei schon große Meilensteine errreicht worden sind, scheint der Weg bis zu diesem Ziel noch weit und stellt eine der großen Herausforderungen der modernen Informatik dar.
Zum Abschluss wollen wir dem Leser noch ein Gefühl für Größenordnungen vermitteln. Die folgende Tabelle enthält Abschätzungen für den Zeitaufwand, eine Zahl, die sich aus 2 großen Primzahlen zusammensetzt, zu faktorisieren. Im unteren Teil haben wir einige markante riesig große Zahlen (Googles) aufgelistet.
| Bezugsgröße | Aufwand / Anzahl |
| Verwendung
des momentan schnellsten Algorithmus und aller heutigen Rechner auf der Erde zur |
|
| Faktorisierung einer 256-stelligen Dezimalzahl | mehr als 2 Monate |
| Faktorisierung einer 512-stelligen Dezimalzahl | mehr als 10 Millionen Jahre |
| Faktorisierung einer 1024-stelligen Dezimalzahl | mehr als 1018 Jahre |
| Lebensdauer des Universums | ≈ 1011 Jahre |
| Taktzyklen eines 5 GHz Prozessors in einem Jahr | ≈ 1,6 · 1017 |
| Anzahl Elektronen im Universum | ≈ 8 · 1077 |
| Anzahl 100-stellige Primzahlen | ≈ 1,8 · 1097 |
| Kombinationsmöglichkeiten bei 400 Münzen | 2400 ≈ 2,6 · 10120 |
- Primzahlen: C. Caldwell, The Prime Pages
- Faktorisierung: R. Weis, S. Lucks, Bigger is better!
- RSA-System: Infoserversecurity,
Heise online
News
- weiterführende Informationsseite der Autoren:
http://www.tcs.uni-luebeck.de/Algorithmik/Einwegfunktion.html

