Autor
Emo Welzl, ETH Zürich
Für die Feuerwehr soll ein neuer Standort gefunden werden, der für die Häuser, für die sie zuständig ist, optimal gewählt ist. Die Qualität des neuen Standorts misst sich an der größten Distanz, die zu einem der relevanten Häuser auftritt, wobei diese größte Distanz natürlich möglichst klein sein sollte. Wir idealisieren die Häuser und den neuen Standort der Feuerwehr zu Punkten in der Ebene und wählen für die Distanz zwischen zwei Punkten deren Abstand. Die Eingabe unseres Problems ist also eine Menge P von Punkten in der Ebene.
Sei für einen Punkt s, als potentiellen Standort, r der größte Abstand, der zu Punkten in P auftritt. Offensichtlich gilt nun, dass der Kreis mit Mittelpunkt s und Radius r alle Punkte in P umschließt.
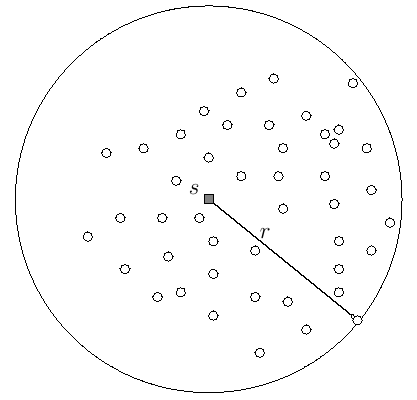
Es wird klar, dass der beste Standort der Mittelpunkt des Kreises mit kleinstem Radius ist, der alle Punkte in P umschließt. Ein solcher kleinster Kreis existiert und er ist eindeutig — nehmen wir das als gegeben hin.

Der Häuser gibt es viele und man überlegt sich wie man den besten Standort bestimmen soll.
Jemand hat die Idee, Vertreter einer kleinen zufälligen Auswahl R1 von, sagen wir, 13 Häusern zusammenkommen zu lassen, um den für sie besten Standort zu ermitteln — ohne jegliche Rücksicht auf die anderen Häuser. Der Vorschlag wird aufgegriffen, das Ergebnis ist ein Standort s1 und ein Radius r1, sodass der Kreis mit Mittelpunkt s1 und Radius r1 alle ausgewählten Häuser umschließt — der kleinste, R1 umschließende Kreis.
Ein erster Standort ist gefunden.
Obwohl die Menge R1 zufällig gewählt wurde, ist der Protest gegen diesen neuen Standort groß, vor allem unter den Besitzern der Häuser, die außerhalb des ermittelten Kreises liegen.
Dem Protest wird stattgegeben, man entschließt sich zu einer zweiten Runde, aber nach wie vor hat man keine Ahnung, wie für die riesige Menge an Punkten der kleinste Kreis berechnet werden soll — für 13 war es schon schwierig genug. Auch der Vorschlag, alle einzuladen, die außerhalb des ersten Kreises liegen, erscheint nicht realistisch. Es kommt zu folgendem Kompromiss: Bei der Verlosung der 13 Vertreter haben alle, deren Häuser außerhalb jenes ominösen Kreises lagen, zwei Zettel im Lostopf.
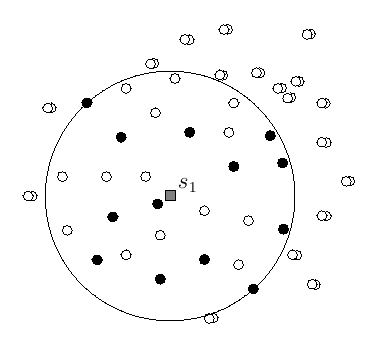
Es werden 13 Vertreter gezogen, die Menge R2, sie treffen sich, bestimmen ihren besten Standort s2 und den entsprechenden Radius r2 des kleinsten Kreises der R2 umschließt.
Wenig verwunderlich, auch dies fordert Widerstand heraus, wieder gibt es viele Häuser, die außerhalb des Kreises der für R2 ermittelten Lösung liegen.
Man muss nun wissen, dass die Gemeindeleitung die Finanzierung des neuen Gebäudes für die Feuerwehr noch nicht gesichert hat. Sie findet daher Gefallen an dem Entscheidungsprozess — d.h. eigentlich Gefallen daran, dass der Prozess wohl nicht so schnell zu einem alle befriedigenden Ergebnis führen kann, wenn überhaupt.
Die Lösung der zweiten Runde wird also wieder verworfen. Für die nächste Runde werden für alle, deren Haus in der zweiten Runde außerhalb des Kreises lagen, die Zettel verdoppelt. Liegt ein Haus in beiden bislang ermittelten Lösungen außerhalb der jeweiligen Kreise, liegen dafür immerhin schon 4 Zettel im Topf!
Runde drei verläuft wie gehabt.
Und so weiter, und so weiter.
Es kehrt Routine ein. Die Kreisfindungstreffen entpuppen sich als beliebte Unterhaltung, auch weil die Gemeinde Speis und Trank zur Verfügung stellt. Außerhalb des jeweils veröffentlichten Kreises zu liegen, wird gar nicht mehr als Enttäuschung empfunden, weil der Vorschlag sowieso nicht realisiert wird, und sich so die Chancen für eine Teilnahme am nächsten Treffen vergrößern. Der Lostopf schwillt an, aber der Gemeindesekretär hat schnell ein elektronisches Losverfahren eingerichtet (animiert durch den 38. Algorithmus der Woche über Zufallszahlen).
Doch dann, nachdem sich wieder einmal 13 Vertreter getroffen haben und die für sich, und nur für sich, beste Lösung vorschlagen, geschieht das eigentlich Unerwartete. Kein Haus liegt außerhalb des berechneten Kreises. Schnell macht die Kunde die Runde, ein eilig bestelltes Gutachten bestätigt, was alle vermutet haben: Das muss jetzt der kleinste alle Punkte umschließende Kreis sein. Schließlich kann der kleinste Kreis, der alle umschließt, nicht kleiner sein, als der, der nur 13 der Punkte umschließt.
Der optimale Standort ist gefunden!
War es Glück, dass das gewählte Verfahren zum Erfolg führte, oder war es zu erwarten? Letzteres: Wir haben einen von Kenneth Clarkson entwickelten randomisierten (d.h. zufallsbasierten) Algorithmus kennengelernt, der für n Punkte den kleinsten umschließenden Kreis berechnet. Man kann zeigen, dass das Verfahren mit Wahrscheinlichkeit 1 diesen Kreis berechnet, die erwartete Anzahl von Runden ist sogar nur logarithmisch in n. Dabei ist es wichtig, dass man die Größe der jeweils zufällig gezogenen Teilmenge, in unserer Geschichte 13, nicht zu klein wählt — aber 13 genügt, unabhängig davon, wie groß n ist. Auch kann man genau so kleinste Kugeln um Punkte im 3-dimensonalen Raum, oder auch in höheren Dimensionen berechnen (nur die zufällige Auswahl muss man abhängig von der Dimension etwas größer wählen).
Wer verwegen genug ist, dem sei noch in groben Zügen verraten, warum das wirklich so klappt. Dazu müssen wir erst die Struktur des Problems etwas besser verstehen. Der kleinste, die Punktemenge P umschließende Kreis — höchste Zeit, dass er einen Namen bekommt: K(P) — ist durch höchstens 3 der Punkte in P bestimmt. Genauer gesagt, es gibt eine Menge B von höchstens 3 Punkten in P, für die K(B) = K(P) gilt. Beachte: wenn für eine Teilmenge R von P nicht schon K(R)=K(P) gilt, dann muss einer der Punkte in B außerhalb von K(R) liegen. In unserem Verfahren heißt das, dass in jeder Runde mindestens einer der Punkte in B seine Zettel im Lostopf verdoppelt und folglich hat nach k Runden mindestens einer von ihnen mindestens 2k/3 ≈ 1.26k Zettel im Topf. Das wächst also ganz ordentlich an.
Andererseits kann man zeigen, dass durch die zufällige Auswahl im Durchschnitt nicht zu viele neue Zettel in den Topf kommen. Es ist ja so, dass genau die Zettel von den Häusern außerhalb des aktuellen Kreises verdoppelt werden. Diese Anzahl ist im Durchschnitt etwa 3z/13, wenn gerade z Zettel im Topf sind (den Beweis für diese Behauptung bleiben wir schuldig). Das heißt, wir erwarten in der nächsten Runde etwa (1 + 3/13)z ≈ 1.23 z Zettel im Topf. (Richtig geraten: die "3" kommt von der Größe von B und die "13" von der Auswahlgröße, für die wir uns entschieden hatten).
Einerseits vermehrt sich also die Anzahl der Zettel pro Runde etwa um den Faktor 1.23, d.h. es gibt etwa n · 1.23k Zettel nach k Runden (n ist die Anzahl der Punkte). Andererseits gibt es einen Punkt, der nach k Runden mindestens 1.26k Zettel im Topf hat. Egal wie groß n ist, das ist wegen 1.26 > 1.23 früher oder später mehr als es insgesamt eigentlich geben dürfte. Es gibt eine einzige Möglichkeit, dieses Paradoxon aufzulösen: Das Verfahren ist vorher zu einem Ende gekommen.
Das ist vielleicht verwirrend. Aber so sind sie nun einmal, die randomisierten Algorithmen: an sich einfach — und zugleich verblüffend, dass es klappt.

