Rene Beier, MPI Saarbrücken
Berthold Vöcking, RWTH Aachen
In zwei Monaten startet die nächste Rakete zur Raumstation. Die Weltraumagentur ist etwas knapp bei Kasse und bietet deshalb kommerziellen Forschungsinstituten an, wissenschaftliche Experimente an der Raumstation durchzuführen zu lassen. Die Rakete kann neben den obligatorischen Verpflegungsrationen noch maximal 645 kg zusätzliche Last mitnehmen, die für die Experimente benutzt werden soll. Die Weltraumagentur erhält von den Forschungsinstituten verschiedene Angebote, in denen steht, wieviel Geld sie für den Transport und die Durchführung des Experiments zu zahlen bereit sind und wie schwer die Geräte für ihr Experiment sind. Welche Experimente soll die Weltraumagentur auswählen, wenn sie den Profit maximieren will?
Hinter diesem Szenario verbirgt sich ein klassisches Problem der Optimierung, das so genannte Rucksackproblem: Wir stellen uns vor, dass wir einen Rucksack haben, der höchstens ein bestimmtes vorgegebenes Gewicht T trägt. T wird als Gewichtsschranke bezeichnet. Neben dem Rucksack gibt es eine Menge von n Objekten (Gegenständen), die jeweils ein Gewicht und einen Profit haben. Wir suchen eine Teilmenge der Objekte, die wir in den Rucksack packen können, ohne die Gewichtsschranke T zu verletzen, so dass der Gesamtprofit möglichst groß ist, also die Summe der Profite der eingepackten Objekte maximiert wird.
Im obigen Beispiel steht der Rucksack symbolisch für die Rakete und hat eine Gewichtsschranke von T = 645. Die Objekte repräsentieren die Experimente. Wir konkretisieren dieses Beispiel und stellen uns vor, dass n = 8 Objekte (Experimente) mit den folgenden Gewichten und Profiten vorliegen.
| Objekt-Nr. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Gewicht in kg | 153 | 54 | 191 | 66 | 239 | 137 | 148 | 249 |
| Profit in 1000 Euro | 232 | 73 | 201 | 50 | 141 | 79 | 48 | 38 |
| Profitdichte | 1.52 | 1.35 | 1.05 | 0.76 | 0.59 | 0.58 | 0.32 | 0.15 |
Intuitiv erscheint es sinnvoll, diejenigen Objekte zuerst auszuwählen, die den größten Profit pro Gewichtseinheit erzielen. Dieses Verhältnis zwischen Profit und Gewicht eines Objektes bezeichnet man auch als Profitdichte. Wir haben in der Tabelle die Profitdichten berechnet und die Objekte bereits so in der Tabelle angeordnet, dass die Profitdichte von links nach rechts immer kleiner wird.
Unser erster Algorithmus startet mit dem leeren Rucksack und fügt die Objekte nacheinander in den Rucksack ein. Dabei berücksichtigen wir zunächst die Objekte, die eine höhere Profitdichte haben. Wir stoppen, sobald das nächste Objekt nicht mehr in den Rucksack passt. In unserem Beispiel würden wir also nacheinander die Objekte 1, 2, 3 und 4 einpacken. Diese haben zusammen ein zulässiges Gewicht von 464. Nummer 5 können wir nicht mehr einpacken, da dann das Gesamtgewicht mit 464 + 239 = 703 die Kapazität des Rucksacks von 645 überschreitet. Die vier Objekte im Rucksack erzielen zusammen einen Profit von 556. Ist das die beste Möglichkeit den Rucksack zu packen? Offensichtlich nicht, denn wir könnten zusätzlich noch Nummer 6 einpacken. Dann enthält unser Rucksack ein Gewicht von 601 und erzielt einen Profit von 647. Ist dies nun die beste Lösung? - Leider nein!
Um garantiert die beste Lösung zu finden, kann man einfach alle möglichen
Kombinationen den Rucksack zu bepacken ausprobieren. Leider gibt es sehr viele
Kombinationsmöglichkeiten. Für jedes Objekt ist zu entscheiden, ob es in den
Rucksack gepackt wird oder nicht. Pro Objekt sind das zwei Möglichkeiten. Bei
n Objekten ergeben sich insgesamt 2n Kombinationsmöglichkeiten. In
unserem Beispiel sind das 28 = 256 Möglichkeiten, die überprüft
werden müssen. Wir können all diese Kombinationen graphisch in einem
Gewicht-Profit Diagramm darstellen: Für jede Teilmenge von Objekten
zeichnen wir entsprechend ihres Gewichts und ihres Profits einen Punkt,
zum Beispiel für die Teilmenge {1,2,3,4,6} den Punkt (601,647).

Jeder Punkt repräsentiert eine Möglichkeit den Rucksack zu packen. Allerdings sind diejenigen mit Gewicht größer als 645 zu schwer für den Rucksack. Das sind gerade die Punkte, die rechts von der roten Linie sind. Punkte, die links oder auf der schwarzen Linie liegen, sind zulässig. Von all den zulässigen Punkten möchten wir denjenigen mit dem größten Profit auswählen. Dieser Punkt entspricht der Teilmenge mit den Objekten 1, 2, 3 und 5, die zusammen Gewicht 637 und Profit 647 haben. Diese ist die so genannte optimale Lösung.
Man kann die optimale Lösung offensichtlich finden, indem man alle Teilmengen ausprobiert. Dieser Algorithmus hat allerdings einen großen Nachteil. Steigt die Anzahl der Objekte nur leicht an, so "explodiert" die Anzahl der Teilmengen. Erhält die Weltraumagentur in unserem Beispiel 60 Angebote für Experimente, so gibt es bereits
(also mehr als eine Trillion) verschiedene Möglichkeiten, eine Auswahl zu treffen. Wenn man optimistisch annimmt, dass ein Computer eine Milliarde Teilmengen pro Sekunde testen kann, so benötigt er trotzdem noch über 36 Jahre, um alle Teilmengen durchzuprobieren. So lange wollen wir den Start der Rakete aber nicht verzögern.
Pareto-optimale Punkte
Wie kann man die optimale Lösung schneller finden? Die Grundidee für einen effizienteren Algorithmus basiert auf folgender Beobachtung: Eine Teilmenge von Objekten kann nicht optimal sein, wenn es eine andere Teilmenge gibt, die leichter (oder gleich schwer) ist und gleichzeitig einen größeren Profit hat. Eine solche Lösung wäre unabhängig von der Gewichtsschranke des Rucksacks immer besser.
Schauen wir noch mal auf unser Beispiel:

Die blauen Punkte können nicht optimal sein, da wir für jeden blauen Punkt
einen noch besseren Punkt finden können, nämlich einen solchen, der weiter
oben und weiter links im Diagramm ist. Zu den roten Punkten gibt es hingegen
keine anderen Punkte, die links oberhalb dieser Punkte liegen.
Derartige Punkte heißen Pareto-optimal. Eine Teilmenge heißt somit
Pareto-optimal, wenn es keine andere Teilmenge gibt, die leichter (oder gleich
schwer) ist und gleichzeitig einen größeren Profit hat. Nur die 17 roten
Punkte entsprechen Pareto-optimalen Teilmengen.
Bei der Suche nach der besten Lösung können wir uns also auf die Pareto-optimalen Teilmengen beschränken. Aber wie kann man eine Liste aller Pareto-optimalen Teilmengen berechnen, ohne explizit alle möglichen Teilmengen auszuprobieren?
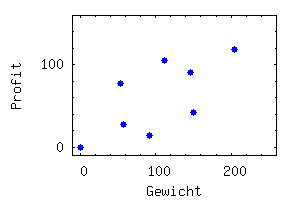
Betrachten wir das folgende kleine
Beispiel mit zunächst nur drei Objekten. Die 23 = 8 verschiedenen
Teilmengen sind wieder in ein Gewicht-Profit-Diagramm eingezeichnet.
Was passiert, wenn man ein zusätzliches viertes Objekt zur Auswahl hat?
Jede der 8 Teilmengen im Diagramm kann man erweitern, indem das vierte Objekt
hinzufügt wird. Somit erhalten wir 8 neue Teilmengen.
Jeder blaue Punkt im Diagramm erzeugt also einen neuen schwarzen Punkt,
der jeweils um denselben Betrag nach rechts oben verschoben ist.
Die Verschiebung nach rechts entspricht dem Gewicht, die nach oben dem Profit
des zusätzlichen vierten Objektes.
Die schwarze Punktmenge ist also nur eine verschobene Kopie der blauen.
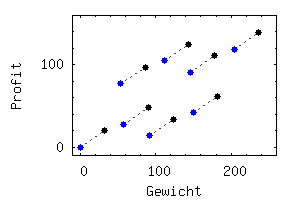
Welche Punkte sind nun Pareto-optimal? Betrachten wir einen blauen Punkt, der nicht Pareto-optimal ist. Dieser wird natürlich auch nicht Pareto-optimal, wenn noch die schwarzen Punkte hinzukommen. Auch der schwarze Punkt, der aus ihm erzeugt wurde, kann nicht Pareto-optimal sein, da man für ihn ja einen anderen besseren schwarzen Punkt finden kann. Man braucht somit nur die Pareto-optimalen blauen Punkte und die aus ihnen erzeugten schwarzen Punkte zu berücksichtigen.
Aus der Liste der Pareto-optimalen Punkte für drei Objekte lässt sich also leicht die Liste für vier Objekte konstruieren. Allgemein, wenn man die Liste für eine Zahl i von Objekten hat, kann man daraus die für ein Objekt mehr, also i+1 Objekte konstruieren: Als erstes erzeugt man dazu alle schwarzen Punkte, die aus den blauen Pareto-optimalen Punkten hervorgehen. Nun muss man diejenigen blauen Punkte löschen, die einen der erzeugten schwarzen Punkte links oberhalb von sich haben und somit nicht mehr Pareto-optimal sind. Umgekehrt muss man nun noch die schwarzen Punkte löschen, die einen blauen Punkt links oberhalb von sich haben. Für i = 0, wenn also gar kein Objekt zur Auswahl steht, gibt es nur den Punkt (0,0), der dem leeren Rucksack entspricht. Dieser Algorithmus wurde schon 1969 von Nemhauser und Ullmann erfunden.
Der Algorithmus von Nemhauser und Ullmann
Die Pareto-optimalen Punkte werden in nach dem Gewicht sortierten Listen verwaltet. Zunächst wird eine Liste L0 erzeugt, die nur den Punkt (0,0) enthält. Dann berechnet man aus der Liste L0 eine neue Liste L1, aus L1 eine weitere Liste L2 usw. bis hin zu einer Liste Ln. Für jedes i von 0 bis n enthält die Liste Li dabei jeweils die Pareto-optimalen Punkte, wenn man nur die Objekte 1 bis i berücksichtigt, also die Objekte i+1 bis n außer Acht lässt.
Die Berechnung der Liste Li+1 aus der Liste Li läuft folgendermaßen ab:
- Aus der Liste Li erzeugen wir eine zweite Liste L'i, in der alle Punkte aus Li enthalten sind, wobei wir die Punkte jeweils um das Gewicht des i-ten Objektes nach rechts und um den Profit des i-ten Objektes nach oben verschieben.
- Die Liste Li+1 erhalten wir nun, indem wir die Listen Li und L'i verschmelzen und dabei diejenigen Punkte streichen, für die es in der jeweils anderen Liste mindestens einen Punkt gibt, der links oberhalb dieses Punktes liegt.
Die zuletzt erzeugte Liste Ln enthält alle Pareto-optimalen Punkte, wenn man alle Objekte berücksichtigt. Zum Schluss wird in Ln derjenige Punkt bestimmt, der das höchste Gewicht nicht größer als T hat. Die zu diesem Punkt gehörende Teilmenge von Objekten ist die gesuchte optimale Lösung.
Ist dieser Algorithmus jetzt besser als das Ausprobieren aller Teilmengen? - Nicht in jedem Fall. Es kann nämlich passieren, dass alle Teilmengen Pareto-optimal sind. Dies passiert beispielsweise, wenn alle Objekte dieselbe Profitdichte haben und gleichzeitig alle Teilmengen unterschiedliche Gewichtswerte haben. In typischen Anwendungen ist dies aber nicht der Fall. Häufig ist die Anzahl der Pareto-optimalen Teilmengen wesentlich geringer als 2n. In unserem Beispiel haben wir die Gewichte und Profite der acht Objekte zufällig erzeugt. Nur 17 der 256 Teilmengen sind Pareto-optimal. Um die Anzahl der Pareto-optimalen Teilmengen abzuschätzen, gibt es einige experimentelle und mathematische Analysen. Aus diesen Analysen folgt, dass typischerweise nur ein äußerst kleiner Bruchteil der Teilmengen Pareto-optimal ist. Deshalb lassen sich mit dem beschriebenen Algorithmus ohne Weiteres Probleme mit mehreren Tausend Objekten lösen.
- Artikel in der Wikipedia zum Rucksackproblem
- Ein englischsprachiges Lehrbuch zum Rucksackproblemen
- Artikel in der Wikipedia zu Pareto-Optimierung

